Que de fois ne voit-on pas ici, en Belgique, une étude de fonction établie sur un canevas bien précis avec notamment étude du signe des dérivées première et seconde (pourquoi pas deuxième ?) et en fin du travail: pas de graphique par manque de temps !

La recherche des asymptotes est presque toujours limitée aux droites. Pourtant il serait utile de se poser d'autres questions. En effet dans la pratique, les fonctions étudiées représentent des phénomènes physiques et bien souvent la variable \(x\) n'est autre que le temps. Dès lors on comprend l'importance du comportement asymptotique des fonctions.

L'étude du signe des dérivées conduit à la résolution d'équations généralement insoluble par les méthodes connues des élèves. Alors, on utilise une calculette pour trouver des solutions approchées. Dès lors, si on accepte le recours à l'informatique, pourquoi ne pas utiliser un petit logiciel de traçage ? Il va de soi que, si on désire un graphique bien précis, il existe des outils informatiques adaptés à ce genre de problème.

Ce qu'on est en droit d'exiger, sans intervention informatique, c'est la description de l'allure du graphique. Outre l'étude du comportement asymptotique, il est également fort utile de pouvoir construire le graphique d'une fonction à partir d'autres plus simples.

Nous prendrons deux exemples fort différents.

Tout d'abord une fonction algébrique, tout ce qu'il y a de plus classique:

\[f(x) = (x^3 + 2)/(x-1)\]

Pas grand chose à dire sur le domaine de définition, sinon qu'il n'existe qu'une seule valeur critique \(x = 1\) pour laquelle seul le dénominateur s'annule et la fonction est donc infinie et il y a une asymptote verticale. On peut encore préciser qu'à gauche de 1 elle est négative et à droite elle est positive, donc elle sautera de \(-\infty\) à \(+\infty\). Elle s'annule quand \(x\) égale la racine cubique de -2. Pas d'asymptote, ni horizontale, ni oblique.

Passons donc à la dérivée première. Après calcul on trouve \(f'(x) = (2x^3 - 3x^2 -2)/(x - 1)^2\). Pas de chance s'il n'y a aucun problème avec le dénominateur toujours positif sur le domaine de définition, par contre le numérateur est un polynôme du 3e degré et il n'est pas évident de trouver les valeurs de x qui l'annulent; en tâtonnant, il semble y avoir un zéro dans l'intervalle \(]0, 1[\). Peut-être aura-t-on le temps de préciser, mais voila, Il faut encore s'attaquer à la dérivée seconde qui s'annonce encore plus corsée. Saura-t-on l'étudier ? Et cela ne fait que commencer: il faudra encore tracer le graphique. Autant jeter l'éponge tout de suite !

Voyons si l'on ne peut pas s'en tirer autrement. Il s'agit d'un quotient de deux polynômes. Pourquoi ne pas le calculer ? On obtient comme quotient \(x^2 + x + 1\) avec un reste égal à 3. La fonction peut se réécrire \(f(x) = x^2 + x + 1 + 3/(x - 1)\); voila qui est plus sympathique. On peut alors écrire \(f(x) = g(x) + h(x)\) avec \(g(x) = x^2 + x + 1\) et \(h(x) = 3/(x - 1)\). La fonction \(g(x)\) a pour graphique une parabole possédant un minimum en \(x = -1/2\) égal à 3/4; avec un ou deux points supplémentaires il n'y a plus aucune difficulté pour tracer son graphique. De plus, si l'on souhaite plus de précision, n'oublions pas que le calcul d'un point pour \(x = x_0\) donne automatiquement un second point pour \(x = -1-x_0\). Passons à \(h(x)\). Il n'y a aucune difficulté pour en tracer le graphique. En décalant l'axe \(y\) sur \(x = 1\) (l'asymptote verticale), on se ramène à une fonction du type \(3/x'\) , c'est-à-dire au graphique de \(1/x\) multiplié par 3. C'est une hyperbole ayant pour asymptote verticale \(x = 1\) et l'axe des \(x\) comme asymptote horizontale. Si la variable \(x\) tend vers l'infini (positif ou négatif) \(h(x)\) tend vers 0 et \(f(x)\) tend vers \(g(x)\). Cela signifie que lorsque \(x\) tend vers l'infini, le graphique de la fonction tend vers la parabole. N'est-ce pas là une asymptote ? C'est ce qu'on appelle une courbe asymptote.

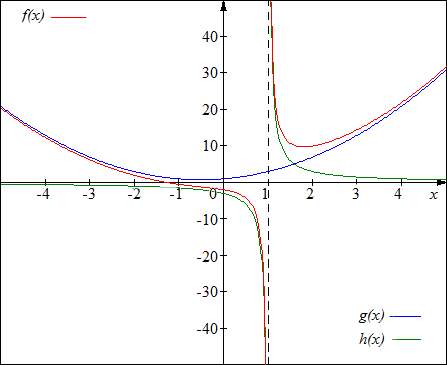
Pour achever le graphique il suffit de dessiner la parabole et de la "corriger" en ajoutant l'hyperbole dont la contribution est négligeable quand \(x\) est assez grand en valeur absolue, mais par contre très importante au voisinage de \(x = 1\).

Une remarque importante: nous venons d'obtenir une courbe asymptote, c'est-à-dire une fonction g(x) telle que la différence entre \(f(x)\) et \(g(x)\) tend vers 0 lorsque \(x\) tend vers l'infini (positif ou négatif dans notre cas).

Au cas où il n'existerait pas de courbe asymptote, il est également important de reconnaître le type de croissance asymptotique de la fonction: elle se comporte comme un polynôme de degré 2, 3, ... n, comme une exponentielle, un logarithme, une sinusoïde, ... Cela signifie qu'il faut trouver une fonction \(k(x)\) (une des plus simples) telle que le rapport \(f(x)/k(x)\) tende vers 1 lorsque \(x\) tend vers l'infini. Un exemple: si \(f(x)\) est un polynôme de degré \(n, ax^n +...\) , tous les polynômes de degré n ayant le même terme en \(x^n\) répondent à la question, mais on choisira évidemment \(k(x) = ax^n\).

Certes, il s'en trouvera pour critiquer cet exemple. Et si l'on avait pris la fonction \((x - 1)/(x³ + 2)\), la méthode aurait-elle échoué ? Pas certain. Il est vrai que le calcul de la division n'est plus possible, mais alors il suffit d'inverser la fonction et on se retrouve dans la situation qui vient d'être étudiée. Dès lors, il n'est pas difficile d'évaluer le graphique de la fonction donnée à partir de celui trouvé plus haut.

Pour d'autres fonctions algébriques comprenant une racine carrée, voir la suite !

Voici à présent une autre fonction, moins traditionnelle, mais fort simple: \(f(x) = x².cos x\).

A nouveau, aucune difficulté ni pour le domaine de définition, ni pour les zéros. Calculons la dérivée première; \(f'(x) = 2x.cos x - x².sin x\) et ses zéros. On trouve immédiatement \(x = 0\) et les autres sont solutions de l'équation \(2cos x -x.sinx = 0\). Nous voilà à nouveau coincés car nous ne pouvons obtenir les solutions que par approximation. Inutile d'aller plus loin. Ne serait-il pas plus simple d'écrire \(f(x) = g(x).h(x)\) avec \(g(x) = x²\) et \(h(x) = cos x\) ? Nous sommes alors face à deux fonctions \(g\) et \(h\) que nous connaissons bien. Le graphique de \(g\) est une parabole, celui de \(h\) une cosinusoïde. La fonction \(f\) est le produit des deux. Comme \(cos x\) oscille entre -1 et +1, le graphe sera compris entre ceux de \(x^2\) et \(-x^2\). Cette remarque nous permet d'en déduire l'allure du graphique de \(f(x)\).

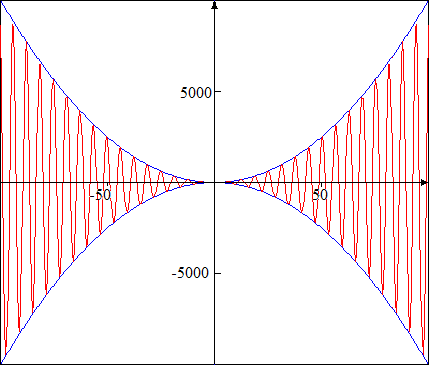
Pour des petites valeurs de \(x\), ce graphique est évidemment imprécis. Il suffit alors de le faire de manière plus affinée en utilisant soigneusement les graphiques des fonctions \(g\) et \(h\).

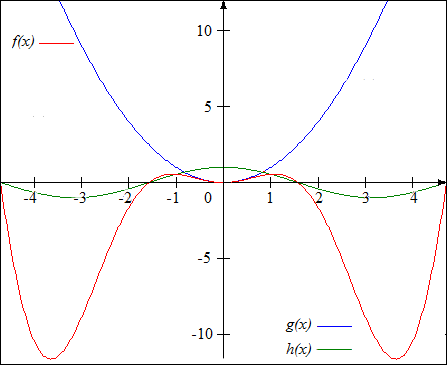
Dans cet exemple, les dérivées, même la dérivée première, ne nous auront donc été d'aucune utilité !