La plupart des fonctions étudiées sont données sous la forme \(y = f(x)\) et leur graphique est une courbe représentée dans un système d'axes \(Oxy, \Bbb R × \Bbb R.\)

Si l'on s'intéresse au mouvement d'un point dans le plan, sa trajectoire est souvent représentée par une courbe définie sous la forme \(x = x(t), y = y(t)\) où \(t\) est le temps ; à chaque instant \(t_0\) correspond le point de coordonnées \((x_0, y_0)\) où \(x_0 = x(t_0\)) et \(y_0 = y(t_0)\).

Il existe également des problèmes pour lesquels un autre système de coordonnées est mieux adapté. Il s'agit des coordonnées polaires.

Tout d'abord, s'il s'agit d'étudier une fonction d'une variable qui représente un angle \(\theta\), il n'est pas très logique de travailler avec un système de coordonnées cartésiennes, c'est-à-dire dans \(\Bbb R × \Bbb R \). En effet, la valeur de la fonction varie dans \(\Bbb R\) (sur un axe), mais la variable varie dans \( \Bbb R /2\pi\), c'est-à-dire sur un cercle. La logique demanderait de travailler dans \(\Bbb R × R/2\pi\), produit d'une droite par un cercle, un cylindre, ce qui n'est toutefois pas très commode, bien qu'on puisse le dérouler sur un plan.

Il existe une autre solution ; il s'agit des coordonnées polaires.

Ce système de coordonnées polaires est défini par une origine (parfois appelée pôle) et un axe (passant par l'origine). Un point peut alors y être représenté par deux nombres \(\rho\) et \(\theta\) où \(\rho\) est la distance à l'origine calculée sur un axe passant par le point et \(\theta\) l'angle que cet axe forme avec l'axe de référence. Nous avons déjà rencontré le graphe de \(\mathbf{sin~}\theta\) et de \(\mathbf{cos~}\theta\) qui prend une forme particulièrement agréable dans ce système de coordonnées.

Ces deux coordonnées dans un plan font penser à la représentation goniométrique des nombres complexes par la formule de Moivre où tout nombre complexe peut être défini à l'aide de son module \(r\) (distance à l'origine) et son argument \(\omega\) (angle du vecteur avec l'axe des réels). Toutefois, il y a une différence essentielle avec les coordonnées \(\rho , \theta\) car \(\rho\) peut être éventuellement négatif ! En effet, \(\rho\) représente la distance à l'origine sur un axe, donc sur une droite orientée.

Avec les coordonnées polaires, tout point du plan (à l'exception de l'origine) peut être décrit de 2 manières différentes : (\(\rho, \theta\)) ou (-\(\rho , \theta + \pi)\). Le fait qu'un même point puisse être représenté par deux couples gêne parfois certains. Pourtant cette situation est tout à fait normale et rend mieux compte de la réalité dans l'étude de courbes.

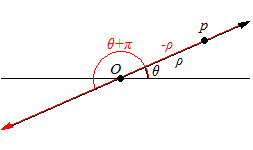
Une manière intuitive de voir les choses est de s'imaginer le plan en tant que plan de symétrie d'un cône de révolution centré à l'origine. 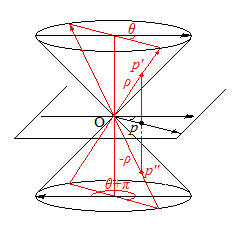Dans le schéma ci-contre, nous avons exagéré l'inclinaison de l'axe afin de mieux voir la situation. Un point du cône sera repéré par la distance au sommet sur la génératrice (on supposera que toutes les génératrices sont orientées vers le haut) et l'angle formé par la génératrice avec l'image de l'axe du plan. A tout point p du plan, correspondent 2 points du cône : les intersections avec la perpendiculaire au plan passant par p. Soit p' et p" ces deux points de percée ; au point p' correspondront les coordonnées (ρ, θ) et au point p" les coordonnées (-ρ, θ+π).

Voici la courbe dont l'équation en coordonnées polaires est :

\[\rho = 1 - 2 \mathbf{sin~}\theta \]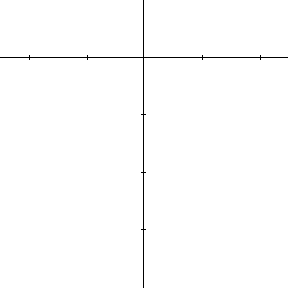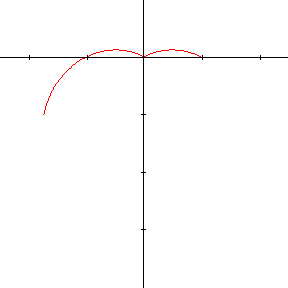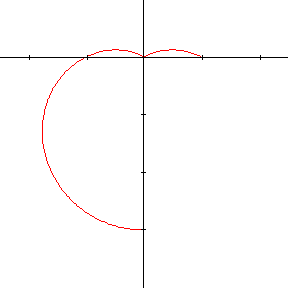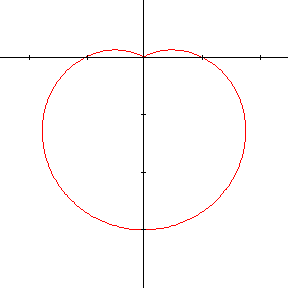

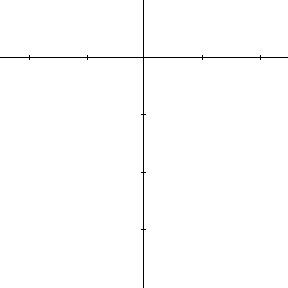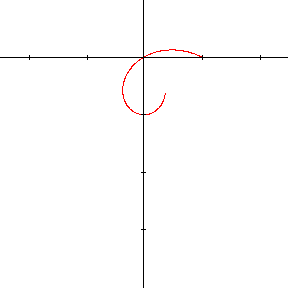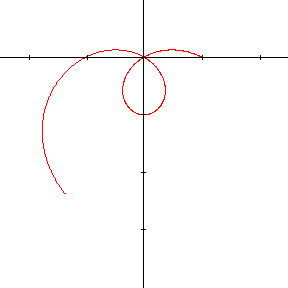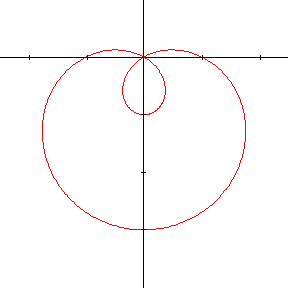
Si l'on exigeait que \(\rho\) soit toujours positif, le tracé s'interromprait chaque fois que \(1-2 \mathbf{sin~}\theta < 0\), c'est-à-dire lorsque \(\pi/6 < \theta < 5\pi/6\) et on obtiendrait la courbe de gauche. On remarque qu'à l'origine, la seconde courbe présente un point anguleux. L'origine correspond à la valeur 0 de \(\rho\), ou encore \(\theta = \pi/6\) et \(\theta = 5\pi/6 \) ; la courbe possède en ce point 2 tangentes distinctes. Bien que la fonction qui définit la courbe soit continue, tout comme ses dérivées, la pente de la tangente présente une discontinuité !

Par contre, si l'on n'impose pas cette condition, on obtiendra la courbe de droite qui est parfaitement continue et dont la tangente varie également continûment.

Un autre exemple : la courbe dont l'équation en coordonnées polaires est :

\[ \rho = \mathbf{cos~}2\theta / \mathbf{cos~}\theta \]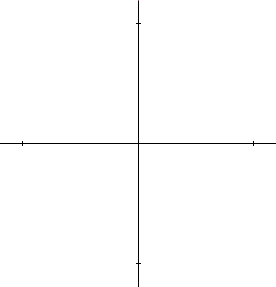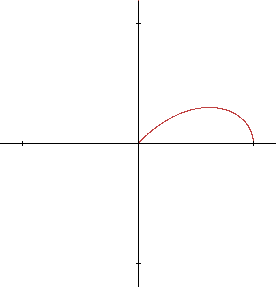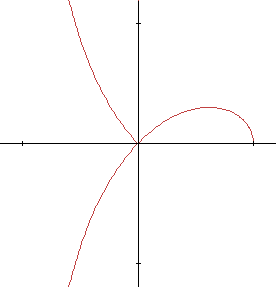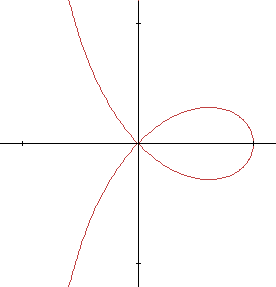

La courbe est tracée en faisant varier \(\theta\) de 0 à \(2\pi\). Si l'on exige \(\theta > 0\), le tracé s'interrompt chaque fois que \(\mathbf{cos~}2\theta / \mathbf{cos~}\theta < 0\). Cette situation se produira lorsque :

\(\pi/4 < \theta < \pi/2  \text{  ou  }  3\pi/4 < \theta < 5\pi/4  \text{   ou  }  3\pi/2 < \theta < 7\pi/4\)

Par contre, si l'on admet que ρ puisse être négatif, la situation est toute différente :

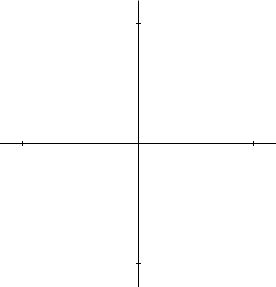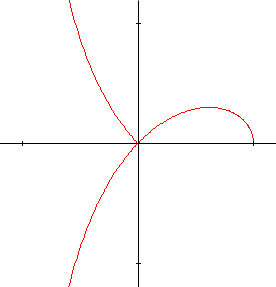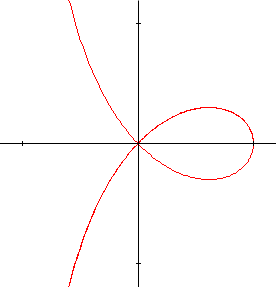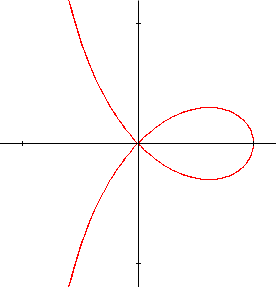
On constate alors que cette courbe appelée strophoïde, possède une tangente dont la pente varie continûment. On remarque également que le tracé de la courbe est effectué deux fois. On peut donc borner la variation de \(\theta\) à un intervalle d'amplitude \(\pi\). En effet, si \(\theta\) augmente de \(\pi\), on vérifie que \(\mathbf{cos~}2(\theta + \pi )/\mathbf{cos~}(\theta +\pi) = -\mathbf{cos~}2\theta / \mathbf{cos~}\theta \). On voit ainsi que \(\rho (\theta + \pi) = -\rho (\theta)\). Il en résulte que le point de coordonnées \((\rho,\theta)\) est identique au point \((-\rho, \theta + \pi)\).

La situation est donc bien plus agréable lorsqu'on admet toutes les valeurs réelles de \(\rho\).

Affichons quelques exemples de jolies courbes définies en coordonnées polaires par des équations fort simples :

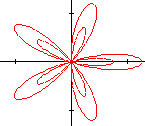
\( \rho = \mathbf{sin~}2t/3\)	\( \rho = \sqrt{ \mathbf{tg~}2t}\)	\( \rho = 1/4 + \mathbf{cos~}5t\)
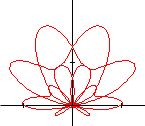
\( \rho = \mathbf{sin~}4t/\mathbf{sin~}t\)	\( \rho = \sqrt{\mathbf{cos~}2t}\)	\( \rho = \mathbf{sin} t+(\mathbf{sin~~ }(5t/2)^3\)

Terminons en signalant que ce système de coordonnées est très utile dans des problèmes de mécanique où un seul point est privilégié ; par exemple l'orbite des planètes ou des comètes autour du soleil.

L'équation de ces trajectoires coniques est fort simple lorsqu'on utilise le soleil comme origine : avec un bon choix de l'unité, elles peuvent s'écrire :

\[\rho = \frac{1}{1 -\varepsilon~\mathbf{cos~}\theta}\] où \(\varepsilon\) est l'excentricité de la trajectoire.

Si \(\varepsilon = 0\), on obtient le cercle, \( 0\lt \varepsilon \lt 1\) donne les différentes ellipses, pour \(\varepsilon = 1\) on obtient la parabole (toutes les paraboles sont semblables !) et \( \varepsilon\gt 1\) donne toutes les hyperboles.