On enseigne en goniométrie les célèbres formules de Simpson:

\[ \mathbf {sin~}p+\mathbf {sin~}q=2~\mathbf {sin~}\frac{p+q}{2}\mathbf {cos~}\frac{p-q}{2}\] \[ \mathbf {sin~}p-\mathbf {sin~}q=2~\mathbf {cos~}\frac{p+q}{2}\mathbf {sin~}\frac{p-q}{2}\] \[ \mathbf {cos~}p+\mathbf {cos~}q=2~\mathbf {cos~}\frac{p+q}{2}\mathbf {cos~}\frac{p-q}{2}\] \[ \mathbf {cos~}p-\mathbf {cos~} q=-2~\mathbf {sin~}\frac{p+q}{2}\mathbf {sin~}\frac{p-q}{2}\]

Mais pourquoi donc ces formules sont-elles célèbres ?

Avant l'invention des machines à calculer et autres calculettes, les mathématiciens travaillaient avec un calculateur, un assistant qui effectuait les calculs numériques; ceux-ci se faisaient à l'époque de Simpson à l'aide de tables logarithmiques et goniométriques. Or si les logarithmes étaient des outils efficaces pour les calculs de produits et puissances, ils n'étaient pas adaptés lorsqu'intervenaient des sommes. Alors grâce à ces merveilleuses formules, on passait de sommes (ou de différences) à des produits qui, eux, devenaient calculables à l'aide de logarithmes.

Parfait, mais mis à part les exercices conçus dans le but de les utiliser (!), quel est encore l'intérêt de ces formules ? Fort réduit, mais en cherchant bien on peut encore trouver deux applications intéressantes, l'une concernant les oreilles, l'autre les yeux.

Les oreilles

Un son parvient à nos oreilles porté par une onde sinusoïdale dont la fréquence vaut \(\omega\). Que se passe-t-il si l'on perçoit simultanément deux sons de fréquences voisines ? C'est ce qui se passe lorsque l'on accorde un instrument par rapport à un autre.

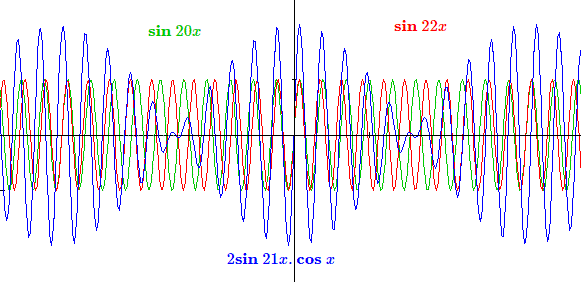
Supposons que les deux sons soient de même amplitude de fréquences \( \omega_1\) et \(\omega_2\). On perçoit donc la somme de deux ondes proportionnelles à \(\mathbf {sin~}\omega_1\) et \(\mathbf {sin~}\omega_2\). En appliquant les fameuses formules de Simpson, on obtient:

\[\mathbf {sin~}\omega_1 t +\mathbf {sin~}\omega_2 t = 2\mathbf {sin~}\frac{\omega_1+\omega_2}{2}t \mathbf {cos~}\frac{\omega_1-\omega_2}{2}t\]

On voit ainsi que si les deux instruments sont parfaitement accordés, c'est-à-dire \(\omega_1 = \omega_2\), l'onde sonore est simplement d'une amplitude double. Par contre si les instruments ne sont pas exactement accordés, c'est-à-dire s'il existe une légère différence entre \( \omega_1 \text{ et }\omega_2\), le premier facteur donne un son proche des sons émis, mais le deuxième facteur affecte l'amplitude d'une variation appelée battement.

Voici :

1. un son de "La" normalisé à 440hz :
2. un son de "La" à 441hz :

Vous pouvez faire jouer simultanément les deux premiers sons et vous obtenez ainsi :

3. les deux sons émis simultanément:

Au fur et à mesure que l'on ajustera l'accord des deux instruments, la fréquence ( \(\omega_1-\omega_2\)) du battement diminuera jusqu'à devenir nulle, c'est-à-dire que le battement disparaîtra.

Les yeux

Le phénomène de battement peut également être visualisé.

Lorsqu'on circule sur autoroute, il arrive que l'on rencontre un pont qui la surplombe. Lorsque ce pont possède des garde-fous formés de grilles verticales on peut observer un phénomène analogue au phénomène de battement. Lorsqu'on est fort loin du pont, on voit les deux grilles décalées l'une par rapport à l'autre. L'écart entre les barreaux de la grille avant est pratiquement le même que celui entre les barreaux de la grille arrière.

Lorsqu'on se rapproche du pont, l'effet de perspective commence à jouer; l'écartement entre les barreaux de la grille avant (plus proche) nous paraît plus grand que celui entre les barreaux de la grille arrière (plus éloignée). On a en quelque sorte une superposition de deux phénomènes périodiques de fréquences légèrement différentes (on suppose pour simplifier les choses que l'écartement des barreaux de chacun des deux parapets nous apparaît constant) et l'on perçoit l'ensemble des barreaux des deux grilles avec un phénomène périodique de barreaux rapprochés et de barreaux éloignés.

Voilà donc une version visuelle des fameuses formules de Simpson.