On représente toujours, par habitude, les fonctions sinus et cosinus par des graphiques dessinés dans le plan \(\Bbb R^2\).
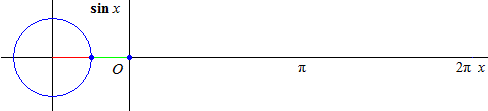
Pourtant ces fonctions associent une valeur réelle \(y\) à un angle \(x\). Il serait dès lors plus logique de faire un graphique où la variable est un angle qui varie autour d'un point ou sur un cercle (lorsqu'on assimile l'arc à l'angle au centre intercepté).
Dans le premier cas on est conduit au graphique en coordonnées polaires
On peut faire de même pour la fonction cosinus ; ce sera également un cercle. Si ensuite par une rotation de \(\pi /2\), on fait coïncider ces deux cercles on obtient la figure ci-dessous.
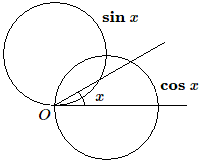
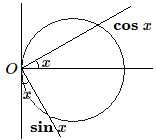
Comme l'angle \(x\) se retrouve à deux endroits, le triangle \(Osc\) est rectangle en \(O\), son hypoténuse est le diamètre et on retrouve le théorème de Pythagore \(\mathbf{sin~}^2 x + \mathbf{cos~}^2 x = 1\).
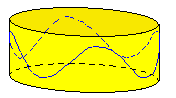
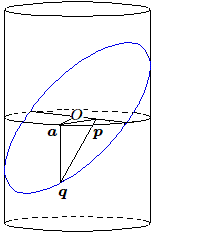Considérons le cas où le graphique se fait sur le produit d'un cercle par une droite, c'est-à-dire sur un cylindre et supposons le rayon du cercle égal à 1.
Si \(O\) est l'origine des arcs et le point \(\boldsymbol{a}\) l'extrémité d'un arc correspondant à l'angle au centre \(x\), \(\boldsymbol{pa}\) vaut le sinus de \(x\). On reporte \(\boldsymbol {qa = pa}\) sur une génératrice. Le triangle \(\boldsymbol {paq}\) est rectangle isocèle et \(\boldsymbol{q}\) est situé dans un plan passant par le diamètre et faisant un angle de 45° avec le plan du cercle. On en conclut que le graphique est une section plane du cylindre, c'est-à-dire une ellipse.
On peut, bien entendu, retrouver le graphique usuel en "déroulant" le cylindre sur le plan tangent en O . De plus on voit que si on projette orthogonalement le cylindre sur ce plan on obtient, au voisinage de O une approximation qui est une droite inclinée à 45°.
La projection a pour équation \(z = x\), qui approche \(z = \mathbf{sin~}x\). On peut alors avoir l'idée d'améliorer l'approximation en enroulant la sinusoïde sur un cylindre plus large et en projetant sur le plan tangent.
Pour que la projection sur le plan Oxy superpose les points 2 à 2 on voit que le rayon du cylindre doit valoir un entier impair 1, 3, 5,... 2n + 1. Examinons les premiers cas ; on a les équations :
\[ \begin{cases} x = 3~\mathbf{sin~}\theta \\ y = 3~\mathbf{cos~}\theta \\ z = \mathbf{sin~}3\theta \end{cases} \hskip5em \begin{cases} x = 5~\mathbf{sin~}\theta \\ y = 5~\mathbf{cos~}\theta \\ z = \mathbf{sin~}5\theta \end{cases} \]En utilisant la formule de Moivre on obtient :
\[ \hskip8em \begin{cases} x = 3~\mathbf{sin~}\theta\\ y = 3~\mathbf{cos~}\theta\\z =3 \mathbf{sin~}\theta - 4~\mathbf{sin~}^3 \theta \end{cases} \hskip4em \begin{cases} x = 5~\mathbf{sin~}\theta\\ y = 5~\mathbf{cos~}\theta\\z =5~\mathbf{sin~}\theta - 20~\mathbf{sin~}^3 \theta + 16~\mathbf{sin~}^5 \theta \end{cases}\]
et les projections orthogonales sur le plan Oxz donnent les approximations :
\[ \hskip4em z = x - \frac {4}{27} x^3 \hskip8em z = x - \frac{4}{25} x^3 + \frac{16}{3125} x^5 \]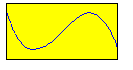
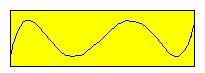
Ces approximations sont de plus en plus précises ; ce sont des polynômes impairs, en fait, des polynomes de Tchebychev. Remarquons qu'il ne s'agit pas des développements de MacLaurin limités, mais les coefficients tendent vers ceux de la série lorsque le degré du polynôme augmente.
Si l'on veut obtenir de semblables approximations pour la fonction cosinus, il suffit de projeter la sinusoïde enroulée sur un cylindre de rayon pair. On obtient de manière analogue :
\[ \begin{cases} x = 2~\mathbf{sin~}\theta \\ y = 2~\mathbf{cos~}\theta\\z = \mathbf{cos~}2\theta \end{cases} \hskip5em \begin{cases} x = 4~\mathbf{sin~}\theta \\ y = 4~\mathbf{cos~}\theta\\z = \mathbf{cos~}4\theta \end{cases} \]En utilisant à nouveau la formule de Moivre on a :
\[ \hskip6em \begin{cases} x = 2~\mathbf{sin} \theta \\ y = 2~\mathbf{cos~}\theta \\ z = 1- 2~\mathbf{sin~}^2 \theta \end{cases} \hskip5em \begin{cases} x = 4~\mathbf\sin \theta\\y = 4~\mathbf\cos \theta\\z = 1 - 8 \mathbf{sin~}^2 \theta + 8~\mathbf{sin~}^4 \theta \end{cases}\]
ce qui donne pour projections orthogonales sur le plan xz les courbes d'équations :
\[ \hskip4em 1- \frac {1}{2}x^2 \hskip6em 1- \frac {1}{2}x^2 + \frac {1}{32}x^4 \]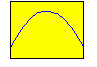
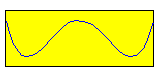
qui constituent de bonnes approximations de la fonction cosinus (à comparer au développement de MacLaurin ).