Un orchestre symphonique s'adresse à un atelier de menuiserie où l'on fabrique des chaises et des pupitres. Deux ouvriers y travaillent à temps partiel, car pour des raisons de disponibilité de matériel, les deux ne peuvent travailler simultanément. Tous deux savent confectionner des chaises et des pupitres, mais Albert est spécialisé dans la confection de pupitres et Bernard dans celle de chaises. Bernard, qui est plus ancien dans la maison, est mieux payé qu'Albert. De manière précise, voici les données par semaine.

	Salaire	# pupitres	# chaises
Albert	1000	10	4
Bernard	1500	5	7

L'atelier reçoit commande de \(50\) pupitres et \(50\) chaises à livrer au plus tard dans \(11\) semaines. Comment répartir le travail ?

Désignons respectivement par \(x\) et \(y\) le nombre de semaines de travail pour Albert et Bernard. L'échéance impose que \(x+y \le 11\) On doit produire \(50\) pupitres, donc \(10x+5y\ge 50\) et \(50\) chaises, donc \(4x+7y\ge 50\) Faut-il le dire, \(x\) et \(y\) sont tous deux positifs.

En résumé nous obtenons un système d'inéquations linéaires:

\[ \begin{array}{lllll} x+y \le 11 \\ 10x+5y\ge 50 \\ 4x+7y\ge 50 \\ x\ge 0 \\ y\ge 0 \end{array} \]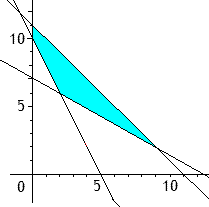

Si nous représentons sur un graphique les contraintes, la partie colorée est l'ensemble de toutes les solutions. Bien entendu, on cherchera à obtenir un bénéfice maximum. On doit minimiser le coût de production: \(1000x+ 1500y\)

Étudions graphiquement la variation du coût. Pour cela supposons que nous nous fixions un coût bien déterminé soit, par exemple, \(3000\). On a donc \(1000x\) \(+1500y=3000\) ce qui est l'équation d'une droite.

Si nous modifions ce coût, par exemple \(4500\), on obtient \(1000x+1500y=4500\), c'est-à-dire l'équation d'une autre droite. Pour toute autre valeur du coût, on obtient une droite et toutes ces droites sont parallèles (on pouvait le prévoir en se rendant compte que les droites ne pouvaient se couper).

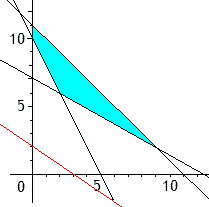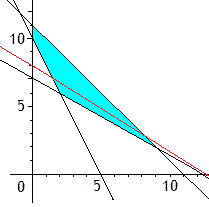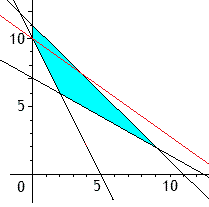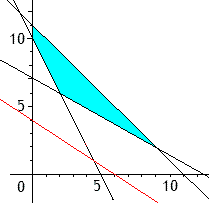
La variation du coût se représente donc, graphiquement, par la translation de la droite \(1000x + 1500x = k\). A l'origine \(x=y=0\) et le coût est nul; au plus la droite s'écarte de l'origine, au plus le coût augmente. On doit donc choisir dans le domaine le point "le plus proche" de l'origine, qui dans notre cas est le point de coordonnées \(x=2\) et \(y=6\).

La solution consiste donc à faire travailler Albert 2 semaines et Bernard 6 semaines. Il en coûtera \(11000\) et le délai sera largement respecté.

Modifions légèrement les données. Supposons que Bernard ne fabrique que \(6\) chaises par semaine. Dans tout ce qui précède, il suffit de remplacer \(7\) par \(6\). Que se passe-t-il ?

Une des droites frontières du domaine est modifiée et la solution optimale devient \(x=1,25\) et \(y=7,5\).

Malheureusement, il y a un problème: toute semaine entamée doit être entièrement payée; autrement dit, il ne faut tenir compte que des solutions en nombres entiers. Que faut-il faire ? Une première réaction est de prendre la solution entière "la plus proche", c'est-à-dire \(x=1\) et \(y=8\). Mais est-ce vraiment la meilleure solution?

Regardons les choses de plus près. Nous ne pouvons en fait considérer que les points à coordonnées entières contenus dans le domaine; nous devrons donc déplacer la droite correspondant au coût minimum parallèlement à elle-même jusqu'à ce qu'elle rencontre un point à coordonnées entières. Ce n'est, en général, pas chose aisée, mais dans notre cas nous pouvons regarder les possibilités point par point. Pour le point de coordonnées (\(1,8\)), le coût est de \(13000\).

Un autre point, qui semble beaucoup plus éloigné est le point (\(2,7\)). Pourtant, surprise ! Le coût est de \(12500\). On peut vérifier sans beaucoup de peine que c'est la solution optimale.