La fonction exponentielle \(\mathbf{exp~}x\) peut notamment être définie par son développement en série de MacLaurin . On a :

\[ \mathbf{exp~}x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\frac{x^5}{5!} +...\]

À partir de cette formule, on démontre aisément les propriétés essentielles de la fonction exponentielle: \(\mathbf{exp~}0=1\); \(\mathbf{exp~}(-x) = 1/\mathbf{exp~}(x)\) ; un peu plus difficile, la relation \(\mathbf{exp~}x.\mathbf{exp~}y=\mathbf{exp~}(x + y)\).

Ces propriétés ne font appel qu'aux propriétés additives et multiplicatives des variables \(x\) et \(x\), c'est-à-dire qu'elles utilisent uniquement le fait que \(x\) et \(y\) sont des éléments d'un corps commutatif. Rien n'empêche donc de parler de la fonction \(\mathbf{exp~}z\), où \(z\) est un élément du corps des complexes. On a:

\[ \mathbf{exp~}ix=1+ix-\frac{x^2}{2!}-i\frac{x^3}{3!}+\frac{x^4}{4!}+i\frac{x^5}{5!}+... \]

ou, en regroupant (sans trop de précautions !) les termes réels et imaginaires:

\[ \mathbf{exp~}ix=1-\frac{x^2}{2!}+\frac{x^4}{4!}+...+ i(x-\frac{x^3}{3!}+\frac{x^5}{5!}+...) \]

On reconnaît les développements en série de MacLaurin des fonctions \(\mathbf{cos~}x\) et \(\mathbf{sin~}x\). On peut donc écrire:

\[ \mathbf{exp~}ix=\mathbf{cos~}x+i\mathbf{sin~}x \]

Comme les propriétés des exponentielles restent valables on a, en particulier :

\[ \mathbf{exp~}(ix + iy) = \mathbf{exp~}(ix).\mathbf{exp~}(iy) \]

On retrouve les formules classiques d'addition des angles par identification des parties réelles et imaginaires :

\[ \mathbf{cos~}(x+y)=\mathbf{cos~}x.\mathbf{cos~}y - \mathbf{sin~}x.\mathbf{sin~}y \]

et

\[ \mathbf{sin~}(x+y)=\mathbf{sin~}x.\mathbf{cos~}y + \mathbf{cos~}x.\mathbf{sin~}y \]

De même, on a la formule de Moivre:

\[ (\mathbf{cos~}\omega+i\mathbf{sin~}\omega)^n= \mathbf{cos~}n\omega+i\mathbf{sin~}n\omega \]

Les nombres complexes représentés par \(\mathbf{exp~}ix\) sont situés sur le cercle unité; ils sont de module 1.

Un nombre complexe quelconque peut donc s'écrire comme produit d'un complexe de module 1 et d'un réel positif. On retrouve ainsi la représentation goniométrique des nombres complexes: \(a + ib = \mathbf{r}(\mathbf{cos~}\omega+i\mathbf{sin~}\omega)\) avec \(\mathbf{r} > 0\). Comme la parenthèse vaut \(\mathbf{exp~}i\omega \), il est bien tentant d'écrire \(\mathbf{r}=\mathbf{exp~}\rho \), ce qui assure le fait que \(\mathbf{r}\) est un réel positif.

En résumé, le nombre \(a+ib\) peut s'écrire sous la forme \(\mathbf{exp~}(\rho+i\omega)\). Il est intéressant de regarder la fonction \(Z(z)\) qui applique \(x+iy\) sur \(\mathbf{exp~}(x+iy)=X+iY\).

La fonction \(Z\) s'exprime sous la forme \(Z(z)=\mathbf{exp~}(x+iy)=\mathbf{exp~}x(\mathbf{cos~}y+i\mathbf{sin~}y)\) ; les lignes coordonnées \(x=x_0\) et \(y=y_0\) sont donc respectivement appliquées sur les cercles centrés à l'origine et sur les demi-droites issues de l'origine.

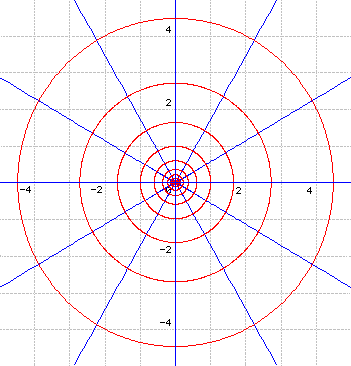
Cette transformation conserve les angles et des courbes orthogonales sont appliquées sur des courbes orthogonales. Remarquons que, suite à la périodicité de la fonction \(\mathbf{exp~}z\), une bande horizontale de largeur \(2\pi\) est appliquée sur tout le plan \(Z\).

Cette application peut être vue de manière dynamique en considérant l' application de \(z\) sur une combinaison de \(z\) et de \(\mathbf{exp~}z\) .

Une autre fonction intéressante à représenter est la fonction \(\mathbf{sin~}z\). Utilisons la formule donnant le cosinus d'une somme: \(\mathbf{sin~}z=\mathbf{sin~}(x+iy)=\mathbf{sin~}x.\mathbf{cos~}iy+\mathbf{cos~}x.\mathbf{sin~}iy\).

Il s'agit à présent de voir le sens à attribuer à \(\mathbf{sin~}iy\) et à \(\mathbf{sin~}iy\). Prenons comme précédemment le développement en série de MacLaurin et nous obtenons:

\[ \mathbf{cos~}iy=1+\frac{y^2}{2!}+\frac{y^4}{4!}+ \frac{y^6}{6!}+ ...\]

ce qui peut s'écrire :

\(\mathbf{cos~}iy=\frac{1}{2}i(\mathbf{exp~}y+\mathbf{exp~}(-y)\)

De même on a:

\[ \mathbf{sin ~}iy=i(y+\frac{y^3}{3!}+\frac{y^5}{5!}+\frac{y^7}{7!}+...) \]

ce qui s'écrit : \(\mathbf{sin~}iy=\frac{1}{2}i(\mathbf{exp~}y-\mathbf{exp~}(-y)\)

En utilisant ces résultats on peut réécrire la formule :

\[ \small\mathbf{sin~}z=\mathbf{sin~}x.\mathbf{cos~}iy + \mathbf{cos~}x.\mathbf{sin~}iy= 1/2(\mathbf{sin~}x.(\mathbf{exp~}y+\mathbf{exp~}(-y)) +i\mathbf{cos~}x.(\mathbf{exp~}y-\mathbf{exp~}(-y))) \]

L'application de \(z\) sur \(\mathbf{sin~}z\) donne donc lieu à la transformation :

$$ \begin{align} & X=1/2(\mathbf{sin~}x.(\mathbf{exp~}y+\mathbf{exp~}(-y))\\ & Y=1/2(\mathbf{cos~}x.(\mathbf{exp~}y-\mathbf{exp~}(-y)) \end{align} $$

Les lignes coordonnées \(x=x_0\) et \(y=y_0\) sont respectivement appliquées sur des ellipses et des hyperboles ayant mêmes foyers. Ces deux familles de coniques sont orthogonales.

En fait, étant donné la périodicité de la fonction, on applique une portion du plan de la variable \(z=x+iy\) à savoir la bande limitée par les droites \(x=-\pi/2\) et \(x=\pi/2\) sur le plan \(Z=X+iY\).

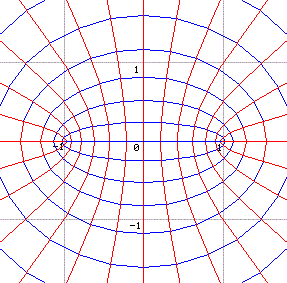
Dans le cas de l'application d'une bande du plan de la variable \(z\) sur tout le plan de la fonction \(Z\), cette application peut être mieux comprise en regardant l' application \(Z=(1-\lambda)z+\lambda\mathbf{sin~}z\) et en faisant varier \(\lambda\) de \(0\) à \(1\). On obtient ainsi une application des deux réseaux de droites orthogonales sur des ellipses et hyperboles homofocales.