Lors de l'étude du plan vectoriel (ou affin centré) muni d'une base \((i, j)\), on rencontre souvent des équations du type:

\[ \begin{cases} x'=ax+by \\ y'=c x+dy \end{cases}\]

Nous nous placerons dans le cas général, celui où l'on peut calculer \(x \text{ et }y\) en fonction de \(x' \text{ et }y'\), le cas où le système formé par les deux équations est inversible.

Que représentent ces équations ?

En voici une première interprétation .

\(x \text{ et }y\) représentent les coordonnées d'un vecteur (d'un point \(P\)) dans le repère donné. \((a, b, c, d)\) définissent une permutation linéaire \(T\) et \((x', y')\) représentent les coordonnées du vecteur (du point \(P\)') transformé de \(X (x, y)\) par la transformation \(T\).

L' application linéaire \(T\) est déterminée par ses coefficients \((a, b, c, d)\) que l'on peut représenter sous la forme d'un tableau dénommé matrice:

\[ \left \lgroup \matrix {a & b \\ c & d} \right\rgroup\]

Mais une matrice est bien plus qu'un simple tableau de nombres. En effet, elle est associée à une transformation et jouit par conséquent de propriétés fort intéressantes. Or on sait que, lorsqu'on se trouve en présence de transformations, on peut les composer. Soit une première transformation \(T\) suivie d'une deuxième \(T'\):

On a:

$$ \begin{align} & x'' = a' x' + b' y' = a' (a x + b y) + b' (c x + d y) = (a' a + b' c) x + (a' b + b' d) y \\ & y'' = c' x' + d' y' = c' (a x + b y) + d' (c x + d y) = (c' a + d' c) x + (c' b + d' d) y \end{align} $$

La transformation \(T''\) composée de \(T\) et de \(T'\) est bien définie et donne ainsi lieu à la définition du produit de deux matrices:

\[ T" = \left \lgroup \matrix {a'' & b'' \\ c'' & d''} \right\rgroup = \left \lgroup \matrix {a' & b' \\ c' & d'} \right\rgroup \circ \left \lgroup \matrix {a & b \\ c & d} \right\rgroup = T' \circ T\]

On retient la règle de multiplication ainsi:

L'élément de la l ^e ligne, m ^e colonne du produit T" de T' et T, s'obtient en faisant la somme des produits des éléments de la l ^e ligne de la première matrice T' par les éléments correspondants de la m ^e colonne de la seconde matrice T.

Quelques remarques:

On voit que, pour faire le produit de deux matrices, il faut impérativement que le nombre de lignes de la première soit égal au nombre de colonnes de la seconde. Cette définition du produit permet alors d'écrire très simplement la situation étudiée. En effet, au point \(P\) de coordonnées \((x, y)\) et à son transformé \(P'\) \((x', y')\) on peut associer les matrices:

\[ P = \left \lgroup \matrix {x\\y} \right \rgroup \text{  et  }P' = \left \lgroup \matrix {x'\\y'} \right \rgroup \]

et la transformation s'écrit de manière compacte:

\[ P' = \left\lgroup\matrix{x'\\y'}\right\rgroup = \left\lgroup\matrix{a & b \\ c & d}\right\rgroup \left\lgroup\matrix{x\\y}\right\rgroup = TP\]

L'intérêt de ces notations est qu'elles peuvent s'étendre à des transformations de vectoriels ayant plus de 2 dimensions.

Remarquons également que si \( x\) et \(y\) sont les coordonnées du vecteur \(\vec{X}\) dans la base B formée des vecteurs \(\vec {\imath} \) et \(\vec {\jmath} \), on peut écrire:

\[ \vec{P} = B P = \boldsymbol{(} i    j \boldsymbol {)} \left\lgroup\matrix{x\\y}\right\rgroup \]

\(B\) est une matrice formée d'une seule ligne alors que \(P\) est une matrice formée d'une seule colonne.

Voici un exemple d'application linéaire :

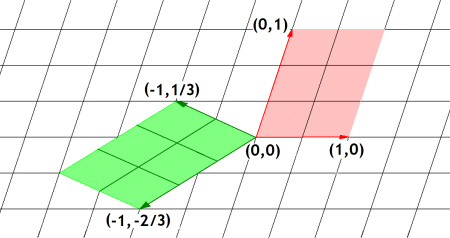
Elle a pour équation :

\[ \begin{cases} x'= -(x+y) \\y'=(x-2y)/3 \end{cases} \]

Nous avons représenté le parallélogramme (rouge) construit sur les vecteurs de base ; dans le repère formé des vecteur de base \(i\) et \(j\), les sommets ont pour coordonnées \((0, 0), (1, 0), (1, 1)\) et \((0, 1)\) et le parallélogramme transformé (vert) a pour sommets les points de coordonnées \((0, 0), (-1, 1/3), (-2/3, -1/3)\) et \((-1, -2/3)\). On voit aisément comment étendre l'application linéaire. Remarquons que le déterminant de la matrice vaut \(1\), ce qui signifie que les aires sont conservées.

A la relecture de cela, on peut toutefois se poser des questions. Un élève attentif aura certainement remarqué tout au début qu'on parle d' un plan vectoriel muni d'une base , expression qu'il rencontre fort souvent à l'occasion d'exercices. Très naïvement, il interrogera son professeur pour savoir qui a muni le (plan) vectoriel d'une base : - Mais, Monsieur, qui a donné cette base : le bon Dieu ? - Bien sur que non, répondra le professeur ! - Mais alors, qui est-ce ? - Bon, dira le professeur excédé, disons que c'est moi. - Ah ! c'est donc vous, notre bon Dieu, répondra l'élève rassuré.

Dès lors, notre élève studieux prendra l'initiative: "Je pourrais donc aussi choisir une base, ou bien encore une autre base". Bref notre élève aura compris que le choix d'une base est absolument libre mais que, par commodité, le mieux est de choisir celle qui rend les calculs les plus simples possibles.

Revenant alors à sa lecture et ayant bien compris comment travailler avec des matrices, il regardera le résultat final. Il y est question d'une unique base B et de deux points, l'un P et l'autre P'. Mais, un point en valant bien un autre, pourquoi ne pas considérer que P et P' sont les mêmes points et qu'on a tout simplement choisi deux bases différentes, l'une B pour P, l'autre B' pour P'. De plus, un changement de base correspond également à une matrice ! En effet, les nouveaux vecteurs de base i' et j' peuvent s'exprimer sous forme de combinaisons linéaires des anciens vecteurs de base. On a :

\[ \begin{cases} i'=a'i+b'j \\ j'=c'i+d'j \end{cases}\]

ce qui peut s'écrire : \( \boldsymbol{(} i' j' \boldsymbol {)} = \boldsymbol{(} i j \boldsymbol {)} \left \lgroup \matrix {a' & b' \\ c' & d'} \right\rgroup \)

Dès lors, on arrive à une deuxième interprétation des mêmes équations : Elles représentent la manière de calculer les coordonnées d'un point dans une base \(B'\) connaissant celles de ce même point dans la base \(B\).

Pour préciser cela on a :

\[ \vec{P} = \boldsymbol{(} i'    j' \boldsymbol {)} \left\lgroup\matrix{x'\\y'}\right\rgroup = \boldsymbol{(} i    j \boldsymbol {)} \left\lgroup\matrix{x\\y}\right\rgroup \] d'où on déduit : \( \boldsymbol{(} i    j \boldsymbol {)} \left\lgroup\matrix{a' & b'\\c' & d'}\right\rgroup \left\lgroup\matrix{x'\\y'}\right\rgroup = \boldsymbol{(} i    j \boldsymbol {)} \left\lgroup\matrix{x\\y}\right\rgroup \)

Comme tout cela est valable quelle que soit la base, on en déduit que :

\[ \left\lgroup\matrix{a & b'\\c' & d'}\right\rgroup \left\lgroup\matrix{x'\\y'}\right\rgroup = \left\lgroup\matrix{x\\y}\right\rgroup \]

et, en posant \( T = \left\lgroup\matrix{a'& b'\\c'& d'}\right\rgroup ^{-1} \), on retrouve sur les équations initiales.

On constate que la matrice du changement de base est l'inverse de celle de la permutation linéaire considérée dans la première interprétation.

Signalons que les mathématiciens privilégient souvent la première interprétation. Par contre, les physiciens s'attachent plus à la seconde interprétation car les résultats des expériences doivent rester inchangés.

Voici un exemple simple à une dimension: la relation \(x'= 100 x \) sera généralement perçue par un mathématicien comme une homothétie de rapport 100 qui multiplie les distances à l'origine par 100, alors qu'un physicien y verra un changement d'unité de mesure, un remplacement par une unité 100 fois plus petite que l'ancienne !

En poursuivant l'analogie avec la physique, on sait que si un observateur (qui se croit fixe) regarde un autre en mouvement rectiligne uniforme, ce dernier (qui se croit également fixe) estimera que le premier effectue un mouvement uniforme en sens inverse. De même, un observateur considérant sa base comme fixe estimera qu'il y a une application linéaire \(T\). Par contre, un observateur lié aux points estimera donc que ce sont les vecteurs de base qui ont subi une transformation linéaire inverse \(T^{-1}\)