Un des objets mathématiques qui nous est le plus familier est incontestablement le cube. Depuis la plus petite enfance nous jouons avec des cubes. Et pourtant, un objet si familier est encore étudié dans les études supérieures. Plaçons nous à mi-chemin, au niveau du secondaire, et voyons ce que nous pouvons en tirer.
Après une première observation, nous constatons qu'un cube possède \(6\) faces (portions de plans) et \(8\) sommets (points); par la suite, notre attention est également attirée par les segments de droite et là, nous dénombrons \(12\) arêtes. Si on le dépose sur une de ses \(6\) faces, il y a \(4\) manières de le tourner et de plus, à chaque fois une symétrie plane est encore possible. Soit \(8\) isométries relatives à la face carrée sur laquelle il est posé et au total \(6 \times 8\) isométries. Quand il est suspendu par un de ses \(8\) sommets, il y a \(3\) rotations et \(3\) symétries, donc au total \(8\times 6\) isométries. Enfin, lorsqu'on le tient par une de ses \(12\) arêtes, il y a \(4\) manières de la conserver et donc au total, pour le cube, \(12 \times 4\) isométries.
Nous pouvons préciser la nature de ces isométries. On peut classer celles-ci en deux types: les déplacements (qui conservent l'orientation, qui transforment une main gauche en une main gauche) et les retournements (qui changent l'orientation, qui transforment une main gauche en une main droite). Les déplacements sont d'une manière générale des vissages (il suffit de songer au tire-bouchon !); mais comme le centre du cube reste fixe, il n'y a que des rotations. Il n'est pas difficile de les dénombrer:
- rotations d'un tiers de tour (dans un sens ou dans l'autre) autour des 4 grandes diagonales; il y en a \(8\)
- rotations d'un quart de tour (dans un sens ou dans l'autre) autour des 3 médianes: elles sont au nombre de \(6\)
- rotations d'un demi-tour autour des 3 médianes: en voila encore \(3\) de plus
- rotations d'un demi-tour autour des droites joignant les milieux de deux arêtes opposées: cela en fait \(6\)
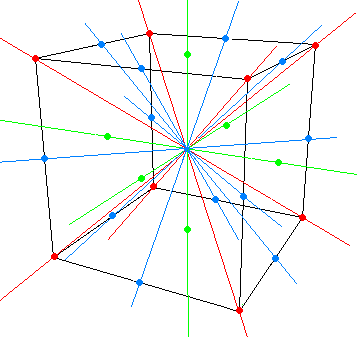
Pour les retournements, le plus simple est d'utiliser la symétrie centrale. En composant celle-ci avec les déplacements énumérés ci-dessus, on obtient les \(24\) retournements du cube. Au total, nous avons donc dénombré \(48\) isométries conservant un cube.
Signalons une petite chanson qui se chante sur l'air de " When the saints go marchin' in " et qui rassemble les principales propriétés du cube:
|
Deux tétraèdres, Trois ax's d'ordre quatre, Quatre ax's d'ordre trois, Six fac's bien planes Mais avec ça, il n'a qu'un centre, C'est bien assez pour mon p'tit cube. Huit sommets pointus, Douze arêt's bien droites, Des déplac'ments, Y'en a vingt-quatre Et quarante-huit isométries, C'est presque trop pour mon p'tit cube |
Soyons sérieux et regardons ce groupe de 48 isométries d'un peu plus près. Comment classer ces 48 isométries ? Plusieurs possibilités s'offrent à nous.
Classer ces isométries par "ordre", c'est-à-dire le nombre de fois consécutives qu'il faut les exécuter pour revenir à l'identité. Toutes les symétries planes axiales ainsi que la symétrie centrale sont d'ordre 2, les rotations autour d'une diagonale sont d'ordre 3, et ainsi de suite. Malheureusement, l'exemple des isométries d'ordre 2 nous montre déjà que cette classification n'est pas très fine.
Une autre manière, plus intéressante, sera de distinguer de grands sous-ensembles d'isométries, par exemple les déplacements et les retournements.
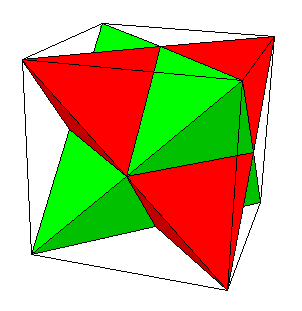
Dans un cube, on peut inscrire deux tétraèdres; on obtient la stella octangula bien connue de Kepler. Ce n'est pas à proprement parler un polyèdre étoilé, mais une imbrication de 2 tétraèdres. Cela permet une autre répartition des isométries; celles qui laissent chacun des deux tétraèdres en place et celles qui les permutent.
Sur base de ces deux critères (fixer F ou permuter P les 2 tétraèdres ainsi que déplacements D et retournements R ), on distingue 4 grandes classes d'isométries conservant le cube.
Schématiquement la situation est:
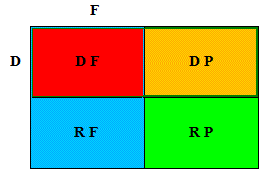
Il est évident que l'ensemble D des déplacements est plus "intéressant" que celui des retournements. En effet, la composition de deux déplacements est encore un déplacement, alors que la composition de deux retournements est un déplacement. Il en est de même avec l'ensemble F des isométries qui fixent chacun des tétraèdres, plutôt que celles qui les permutent.
L'ensemble des isométries qui conservent un cube, et plus généralement l'ensemble des automorphismes d'un être mathématique, forme toujours un groupe. En effet, la composée de deux isométries (resp .de deux automorphismes) est évidemment dans l'ensemble, de même que l'isométrie (resp. l'automorphisme) inverse ou réciproque. Les deux sous-ensembles intéressants D et F sont également des groupes, donc des sous-groupes du groupe C des isométries du cube.
Une petite remarque.
Un ensemble de bijections (isométries, déplacements, permutations de points, de nombres,..) est un groupe , si la composée de deux quelconques appartient à l'ensemble considéré et, dans le cas d'un ensemble infini, si la réciproque lui appartient également. Ce n'est qu'en passant à un ensemble d'êtres munis d'une opération qu'apparaissent des conditions supplémentaires (neutre, réciproque).
Revenons au groupe du cube. D est formé de la réunion de DF et DP . De même, F est formé de la réunion de DF et RF . L'intersection est formée de DF qui est le sous-groupe des déplacements conservant un tétraèdre.
Mais nous n'avons pas encore parlé de RP ! Il s'agit donc des retournements qui permutent les deux tétraèdres. Que se passe-t-il lorsqu'on compose deux de ces permutations ? Le résultat est un déplacement et, évidemment, il fixe les tétraèdres; il appartient donc à DF . De plus il est tout aussi facile de voir qu'en composant une permutation de DF composée avec une de RP , le résultat appartient à RP .
Nous découvrons ainsi un troisième sous-groupe de C : la réunion de DF et de RP . Ce sous-groupe est formé des 12 déplacements conservant chacun des tétraèdres ainsi que des 12 antidéplacements (ou retournements) permutant les deux tétraèdres. Il se rencontre dans la nature dans certains cristaux, en particulier dans la pyrite (sulfure de fer FeS 2 ). Ce corps cristallise dans un système cubique particulier qui ne possède pas toutes les symétries du cube. Si on regarde de près des cristaux cubiques, on remarque que les faces possèdent des stries qui interdisent les quarts de tour. C'est également la raison pour laquelle on rencontre également une forme cristallisée sous la forme de cristaux dodécaédriques .
Ce regroupement d'éléments d'un groupe conduit à un morphisme (à rapprocher de l'étude des isométries d'une sinusoïde ). Le groupe C des isométries du cube contenait 48 permutations. Le sous-groupe D des déplacements du cube et celui F des isométries fixant chacun des tétraèdres contiennent chacun 24 permutations. Le troisième sous-groupe que nous venons de découvrir en contient également 24. Enfin, ces 3 sous-groupes ont en commun l'ensemble DF , les déplacements d'un tétraèdre.
En résumé, on a la structure suivante pour le groupe du cube et ses sous-groupes d'ordre 24 du cube (à remarquer, l'analogie avec celle du groupe des isométries du rectangle).
Voici le tableau qui résume ces propriétés (*)| Ordre 48 |

|
||
| Ordre 24 |

|
|
|
| Ordre 12 |
|
Dans un cube, les 4 diagonales sont permutées de toutes les manières par les 24 déplacements; le groupe des déplacements du cube est Sym(4). Le cube possède un centre de symétrie. La symétrie centrale est un antidéplacement qui commute avec tous les déplacements; le groupe des isométries du cube est donc isomorphe au produit direct Sym(4) × C(2) d'ordre 48. Pour le tétraèdre, le groupe des 24 isométries permute de toutes les manières possibles les 4 sommets; c'est Sym(4). Le sous-groupe des 12 déplacements n'induit sur les 4 sommets que les permutations paires, c'est Alt(4).
Signalons que ces ensembles d'isométries (nous dirions actuellement "sous-groupes") ont été décrits par Léonard de Vinci !
(*) Pour autant que "Java" soit installé sur votre poste de travail, en cliquant sur les images, vous pourrez voir:
- l'ensemble des transformés d'un point "quelconque" de l'espace,
- la figure obtenue en fermant les faces planes du "polyèdre" obtenu.
à l'aide de votre souris, vous pourrez déplacer ces figures planes pour mieux les voir dans l'espace; il y a même moyen de les voir en stéréo ! Voir plus de détails .