Chacune des 10 paires de faces parallèles est colorée de la même manière.

Afin de construire ce polyèdre, un peu plus compliqué que les autres, on peut essayer de reconstituer la partie visible d'une face triangulaire.

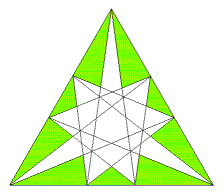
Cette partie est formée de 9 triangles; les 6 triangles passant par les sommets sont isométriques et 3 autres également. En voici un schéma représentant la situation décrite ci-dessus.

On remarque que les points de subdivision des côtés sont tels que le rapport des 3 petits segments aux 6 grands est précisément le nombre d'or \(\tau = (\sqrt{5}-1)/2\). Il est alors aisé de contruire un patron du polyèdre.

La méthode la plus efficace pour un modèle de petite taille semble être la réalisation de 12 petites "pyramides étoilées" qu'on assemble ensuite (ne pas oublier de prévoir des tenons !). Sur les bords d'une étoile on en assemble 5 autres et on fait de même avec les étoiles restantes. On obtient ainsi deux demi-modèles que l'on assemble.