Ce sont les fêtes de fin d'année. On m'a offert une BD (qui n'est pas sur les maths; et pourtant il en existe!). Elle était joliment emballée dans un papier de couleur avec un ruban qui apparaissait aux deux coins opposés.

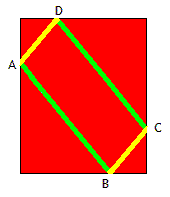
Pour être plus précis, je vous fais un petit dessin. Je vais également dessiner, dans une autre couleur, l'arrière. Voici ce que ça donne:

En regardant la forme dessinée par le ruban, je me suis dit que ce n'était certainement pas un quadrilatère quelconque. Il m'a semblé que le centre du rectangle était aussi le centre de symétrie du quadrilatère et qu'il s'agissait donc d'un parallélogramme. Ça m'avait l'air exact, mais encore fallait-il le démontrer.

Faisons abstraction de l'épaisseur du ruban. Il s'agit donc d'un quadrilatère inscrit dans un rectangle. Cette information est très faible et ne permet certainement pas d'en déterminer la nature. Mais il y a plus précis. Lors de l'emballage, le ruban a été bien serré afin de faire un nœud. Le périmètre de ce quadrilatère est donc le plus petit possible.

Que pouvons-nous en déduire ?

Portons notre attention sur un côté du rectangle; le quadrilatère possède un sommet B. Fixons, provisoirement, les deux sommets adjacents A et C situés sur les deux côtés adjacents du rectangle. Comme la longueur du ruban est minimale, que peut-on dire du point B par rapport aux points A et C ? Le point B doit être tel que la somme des distances AB + BC soit minimum. Partant du point A, on se dirige vers le point B et de là, on rebondit vers le point C.

"Rebondir"! Mais oui, bien sûr ! Cela mous fait penser à la réflexion sur un miroir.

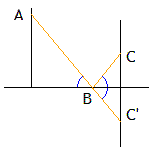Dans ce cas, nous savons comment cela se passe. La lumière suit toujours le chemin le plus court. Partant de A, dessinons le symétrique C' de C par rapport au côté miroir. Le trajet de longueur minimum est le segment AC'. Le point B doit donc se trouver à l'intersection de AC' avec le côté du rectangle; de plus les angles formés par AB et BC avec ce côté sont égaux (voilà la loi de la réflexion !).

Muni de cette information, nous pouvons répéter l'observation pour les autres points, sommets du quadrilatère. Il en résulte de les directions des côtés opposés sont les mêmes et qu'il s'agit donc d'un parallélogramme.

En partant d'un sommet du quadrilatère, on pourrait imaginer que les côtés du rectangle sont des miroirs où un rayon lumineux issu du sommet initial se réfléchit, ou bien encore, les bandes d'un billard sur lesquelles une bille lancée à partir du sommet rebondirait. Toutefois le ruban doit se refermer après 3 bandes; il faut donc bien viser et bien choisir l'angle de départ !

Une manière de procéder est de prendre les symétriques successifs du point A par rapport à chacun des côtés sur lequel il va rebondir. Une autre manière de procéder est de partir du parallélogramme donné et de reconstruire le rectangle. Une fois cela fait, il sera facile de déterminer les relations entre l'angle de visée, les côtés du rectangle et la position d'un point sur le côté. La deuxième méthode semble plus rapide puisque les côtés sont perpendiculaires aux bissectrices des angles du parallélogramme.

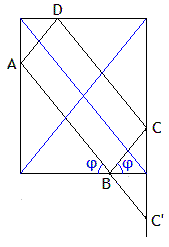Partons donc de la figure formée par le parallélogramme et le rectangle circonscrit. Que se passe-t-il si le point B se déplace sur le côté ? Quelle que soit la position de B sur le côté, AB + BC = AB + BC' (C' le symétrique de C par rapport au côté) qui est précisément la diagonale du rectangle. L'angle φ est donc constant et égal à l'angle de la diagonale.

On voit ainsi qu'étant donné un rectangle et un point sur l'un de ses côtés, le parallélogramme pourra être construit très simplement. Il s'obtiendra en se déplaçant parallèlement aux diagonales du rectangle. La tangente des angles sera égale au rapport des côtés du rectangle. De plus la somme des côtés du parallélogramme (la longueur du ruban d'emballage) sera constante et égale à deux fois la diagonale.

Dans la pratique n'oubliez pas de tenir compte de l'épaisseur (4 fois) ... mais surtout de prévoir une petite réserve afin de faire le nœud !