Le cercle \(\mathbf{C}\) est défini par son centre \(c (a, b)\) et son rayon \(R\). Un point \(p\)\((x, y)\) appartient au cercle \(\mathbf{C}\) si et seulement si \(cp^2= R^2\). Les coordonnées du vecteur \(cp\) sont \((x-a,y-b)\) ; par conséquent l'équation peut s'écrire :
\[(x-a)^2+(y-b)^2 = R^2\]En particulier, si le centre est à l'origine des coordonnées, le cercle a pour équation \(x^2+y^2=R^2\).
En développant l'équation, on obtient :
\[x^2+y^2-2ax-2by+a^2+b^2-R^2 = 0\]Inversement étant donné une équation : \(A(x^2+y^2)+Bx+Cy+D=0\), essayons de la mettre sous la forme ci-dessus.
Si \(A\) = 0, il s'agit de l'équation d'une droite (à condition que \(B\) et \(C\) ne soient pas simultanément nuls). Dans le cas général où \(A\) n'est pas nul,l'équation peut s'écrire :
Cette équation est celle d'un cercle de centre \(C(-\frac{B}{2A},-\frac{C}{2A})\) et de rayon \(\frac{\sqrt{B^2+C^2-4AD}}{2A}\). Ce résultat est à rapprocher de la résolution de l' équation du second degré .
Le cercle n'a pas de point à coordonnées réelles si le radicand est négatif ; il est de rayon nul (réduit à un point) si \(B^2+C^2-4AD=0\). Cette forme quadratique joue un rôle fondamental dans l' étude des cercles .
Lorsque le premier membre de l'équation d'un cercle est écrit de manière à ce que le coefficient de \((x^2+y^2)\) soit égal à 1, on dit que l'équation est mise sous forme normale.
Calculons les intersections du cercle \(\mathbf{C}\) avec une droite passant par le point \(p\) de vecteur directeur unité \(u\).
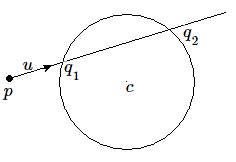Un point quelconque \(q\) situé sur la droite est déterminé par un vecteur \(cq=cp+ \lambda u\) où \(\lambda\) représente la distance du point \(b\)\(p\). Les points d'intersection \(q_1\) et \(q_2\) avec le cercle de centre \(c\) vérifient la condition \(cq^2=R^2\). Les valeurs de \(\lambda\) correspondant aux points d'intersection son déterminées par l'équation :
Les deux valeurs de \(\lambda\) correspondent aux distances du point \(p\) aux deux points d'intersection \(q_1\) et \(q_2\). On constate que le produit de ces distances est constant et vaut \(cp^2-R^2\). Cette constante est appelée puissance du point \(p\) par rapport au cercle \(\mathbf{C}\).
Si le cercle est de centre \(c(a,b)\), on a \(cp^2=(x-a)^2+(y-b)^2\) et la puissance \(\mathbf{P}\) du point \(p\) de coordonnées \(x_0,y_0\) par rapport à \(\mathbf{C}\) vaut :
\[\mathbf{P}=(x_0-a)^2+(y_0-b)^2-R^2\]On voit qu'il suffit de remplacer les coordonnées \((x,y)\) par celles du point \(p\) dans l'équation normale du cercle.
Ce résultat est à rapprocher avec celui donnant la distance d'un point à une droite.
Dans le cas où le cercle est de rayon nul, c'est-à-dire réduit à un point, la puissance n'est autre que le carré de la distance au point. On pourrait donc dire que la puissance est le carré de la distance du point au cercle. Toutefois cette grandeur peut être négative. Cela gêne peut-être certains mathématiciens mais il suffit d'accepter les nombres complexes. Une situation analogue est d'ailleurs rencontrée en relativité.