Tout comme le ruban de Möbius, il s'agit d'une surface unilatère. Cette fois la surface est fermée et ne possède pas de bord.

Elle est obtenue à partir d'un ruban de Möbius en recollant les (ou plus exactement le) bord.

Si le ruban n'était pas tordu, on aurait tout simplement obtenu un tore; mais ici ce sera une sorte de tore qui s'interpénètre pour donner la surface représentée ci-contre.

Tout comme le tore peut être vu comme un cercle tournant autour d'un axe, on peut, tout comme pour le ruban de Möbius, imaginer un chiffre 8 tournant autour d'un axe tout en tournant autour de son centre pour se recoller au bout d'un tour, n'ayant fait qu'un demi-tour.

Les équations paramétriques de cette surface sont : \[ \small \begin{cases} x = (a + \mathbf{cos}(u/2)~\mathbf{sin}(v) - \mathbf{sin}(u/2)\mathbf{sin}(2v))\mathbf{cos}(u) \\ y = (a + \mathbf{cos}(u/2)~\mathbf{sin}(v) - \mathbf{sin}(u/2)\mathbf{sin }(2v))\mathbf{sin }(u) \\ z = \mathbf{sin}(u/2)~\mathbf{sin}(v )+ \mathbf{cos}(u/2)~\mathbf{sin}(2v) \end{cases} \]

Elles dépendent d'un paramètre \(a\) que nous avons choisi égal à 1.

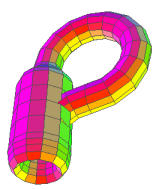
On parle parfois de la "bouteille" de Klein ; il s'agit de la curieuse surface ci-contre ; elle a la même structure topologique. Regardez-la bien nous n'arriverez pas à la remplir ; une mouche pourrait-elle arriver à l'intérieur ?