Par deux points distincts passe une unique droite; par trois points distincts passe une unique parabole! Si la première affirmation est toujours vraie, il n'en est pas de même pour la seconde; on peut tenter de formuler les choses de manière légèrement différente afin que le second énoncé soit valable.

Supposons que l'on connaisse la valeur d'une fonction pour deux réels distincts. On a dans le plan \(x, y\) deux points distincts par lesquels passe une droite unique. Etant donné l'hypothèse faite, cette droite n'est pas parallèle à l'axe \(y\) et son équation peut s'écrire \(y = ax + b\). A présent si l'on se donne trois réels distincts et les valeurs correspondantes de la fonction, on peut vérifier s'il existe une unique parabole \(y = ax^2 + bx + c\) passant par ces trois points.

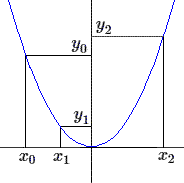
Les inconnues a, b, c sont déterminées par le système:

\[\begin{aligned} y_0 = a x_0^2 +b x_0 + c \\ y_1 = a x_1^2 +b x_1 + c \\ y_2 = a x_2^2 +b x_2 + c \end{aligned} \]

La matrice du système est:

\[ \left\lgroup \matrix {x_0^2 & x_0 & 1 \\x_1^2 & x_1 & 1 \\x_2^2 & x_2 & 1} \right \rgroup \]

Que vaut son déterminant? C'est manifestement un polynôme en \(x_0, x_1, x_2\); ce polynôme est homogène du 3e degré. De plus le déterminant s'annule si \(x_0 = x_1\); il en résulte qu'il est divisible par \(x_0 - x_1\), et de même par \(x_1 - x_2\) et \(x_2 - x_0\). Mais voilà précisément trois facteurs linéaires! Le polynôme est donc connu à un facteur près; un simple coup d'œil montre qu'il vaut \( - (x_0 - x_1)(x_1 - x_2)(x_2 - x_0)\).

Ce déterminant n'est donc jamais nul car les trois valeurs de la variable \(x\) sont distinctes et le système possède une solution unique. (Attention! la parabole peut éventuellement être une droite).

De même si l'on se donne la valeur de la fonction pour quatre réels distincts \(x_0, x_1, x2 et x_3\), il existe une unique parabole cubique \(y = a x^3 + b x^2 + cx + d\) passant par ces 4 points. La démonstration ne fait que généraliser celle donnée plus haut; le déterminant des inconnues \(a, b, c, d\) vaut:

\[\begin{vmatrix}x_0^3 & x_0^2 & x_0 & 1 \\x_1^3 & x_1^2 & x_1 & 1 \\x_2^3 & x_2^2 & x_2 & 1\\ x_3^3 & x_3^2 & x_3 & 1\end{vmatrix} \]

C'est un déterminant de Vandermonde et pour une raison analogue il vaut :

\[ \prod_{i < j} (x_i - x_j) \]

c'est un polynôme de degré n(n+1)/2 qui est nécessairement non nul.

On en conclut que si on désire approcher une fonction donnée on peut faire coïncider une fonction \(y = P(x)\), polynomiale de degré n en n + 1 points. On conçoit dès lors un espoir d'approcher une fonction par un polynôme de degré infini, ou ce que l'on appelle plus précisément une série.

Toutefois entre les points choisis le comportement de la fonction polynomiale (ou série) peut différer fortement de la fonction donnée. On a donc intérêt à choisir les points extrêmement rapprochés; mais ceci nous conduit à choisir une infinité de points infiniment voisins les uns des autres, c'est-à-dire en fin de compte à n'approcher la fonction qu'au voisinage d'un de ses points.

Analytiquement la donnée de la valeur de la fonction en un point voisin du point \(x_0, f(x_0)\) consistera à se donner la valeur de la dérivée première \(f '(x_0)\) ; la donnée de la valeur en un deuxième point voisin correspondra à la valeur de la dérivée seconde, et ainsi de suite.

On voit ainsi comment motiver le concept de développement en série de Taylor au voisinage de \(x_0\), ou d'abord plus simplement un développement de MacLaurin au voisinage de l'origine. On approche \(y = f(x)\) au voisinage de 0 par un polynôme de degré infini (une série):

\[ y = a + bx + cx^2 + dx^3 +... \]

Si l'on exige qu'en zéro les valeurs de la fonction et de ses dérivées successives coïncident avec celle de la série, on obtient:

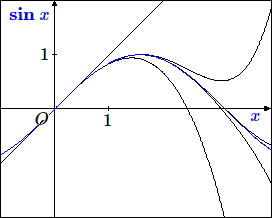
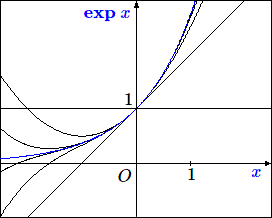
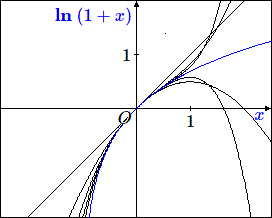
\[ f(x) = f(0)+ f'(0)x + f''(0)\frac{x^2}{2!} + f'''(0)\frac{x^3}{3!} + ...\]

Les figures suivantes montrent des approximations de \(\boldsymbol\sin x, \boldsymbol\exp x\) et \(\boldsymbol\ln (1+x)\) par des développements en série respectivement limités aux cinq premiers ordres. Sur ces figures on pressent que pour \(\boldsymbol\sin x\) et \(\boldsymbol\exp x\), le développement convergera partout. Pour \(\boldsymbol\exp (1+x)\), on devine que le développement ne convergera que dans un voisinage d'amplitude 1 de l'origine (la seule considération de parité des développements successifs montre la divergence pour \(x > 1\). Le problème de la convergence sera étudié avec un peu plus de détails dans l'article consacré aux développements en série de Taylor ou de MacLaurin.