La transformée de Fourier est une brique élémentaire qui trouve son application dans de très nombreuses sciences et problèmes concrets. À l’instar d’une machine à laver qui est constituée de nombreuses pièces dont l’étude peut nous aider à en comprendre le fonctionnement et éventuellement l’améliorer; de nombreux phénomènes physiques s’expriment comme des variations de valeurs dans le temps, des signaux. Afin de comprendre la nature de ces signaux, il est utile de chercher à vouloir décomposer ces signaux complexes en un ensemble de fonctions élémentaires (des sinusoïdes). C’est ce que permet la transformée de Fourier.
Lorsque l’on possède cette décomposition, on est capable de la modifier pour répondre à nos divers besoins. Les exemples classiques sont les filtres, la compression ou la modulation de signaux. Concrètement, on peut imaginer s’en servir pour améliorer la qualité sonore d’un enregistrement en retirant le bruit d’un aspirateur sur une voix. En outre, cette transformée joue un rôle crucial en tant que brique élémentaire dans des problèmes plus complexes tels que l’imagerie médicale, l’astrophysique, la mécanique quantique et encore bien d’autres.
Historiquement, Joseph Fourier a d’abord introduit ses séries (de Fourier) dans le cadre de sa théorie analytique de la chaleur. Dans laquelle, il exprime que n’importe quelle fonction périodique en une variable, quelle soit continue ou discontinue, peut être exprimée comme une série de sinusoïdes pour des multiples de cette variable. Avec le temps, le concept de transformée (de Fourier) s’est précisé et a trouvé des champs d’applications plus larges.
Intuitivement, la série de Fourier fournit la fréquence de réponse (frequency response) d’un signal qui se répète, tandis que la transformée de Fourier la fournit également pour des signaux qui ne se répètent pas. Toutes les deux emploient un ensemble de sinusoïdes afin de reconstruire le signal. La différence réside principalement dans l’interférence (constructive ou destructive); plus les fréquences étudiées sont proches, plus les interférences destructives seront nombreuses et on pourra étudier un signal qui ne se répète pas; plus les fréquences sont éparses, plus le signal aura des chances de se répéter.
Définitions
Signal
Un signal est un concept très vaste qui reprend n’importe quelle variation du milieu qui convoie une information. Classiquement, on pense aux signaux audios tels que la voix ou la musique, mais c’est nettement plus large, un tremblement de terre ou des vagues sont aussi des signaux.
On distingue généralement deux grandes familles de signaux, les analogiques (ou continus) pour lesquelles les valeurs peuvent prendre n’importe quelle valeur dans un intervalle continu, et les numériques (ou discrets) où les valeurs ne peuvent faire partie que d’un ensemble fini possible.
Sinusoïde
Les sinusoïdes sont une famille de fonctions périodiques composées de 3 propriétés:
- L’amplitude : souvent assimilée à la force du signal.
- La fréquence : la vitesse à laquelle le signal se répète, cela correspond à la hauteur en acoustique.
- La phase : la position au sein du signal.
Traditionnellement, on note:
$$ y(t) = A \sin(\omega t + \phi) $$où \(A\) est l'amplitude, \(t\) la variable indépendante (souvent le temps), \(\omega\) la fréquence et \(\phi\) la phase. Pour être particulièrement précis, on différencie \(\omega\) la fréquence angulaire exprimée en radians / seconde, de \(f\) la fréquence ordinaire auquel on est habitué.
On retrouve également cette notion exprimée au travers de la formule d’Euler:
$$ y(t) = A e^{i(\omega t + \phi)} = Z e^{i\omega t} $$Un tutoriel écrit par @Aabu aborde bien plus en profondeur la notion de sinusoïdes.
Une question de vraisemblance
Supposons que l’on ait enregistré un signal quelconque:
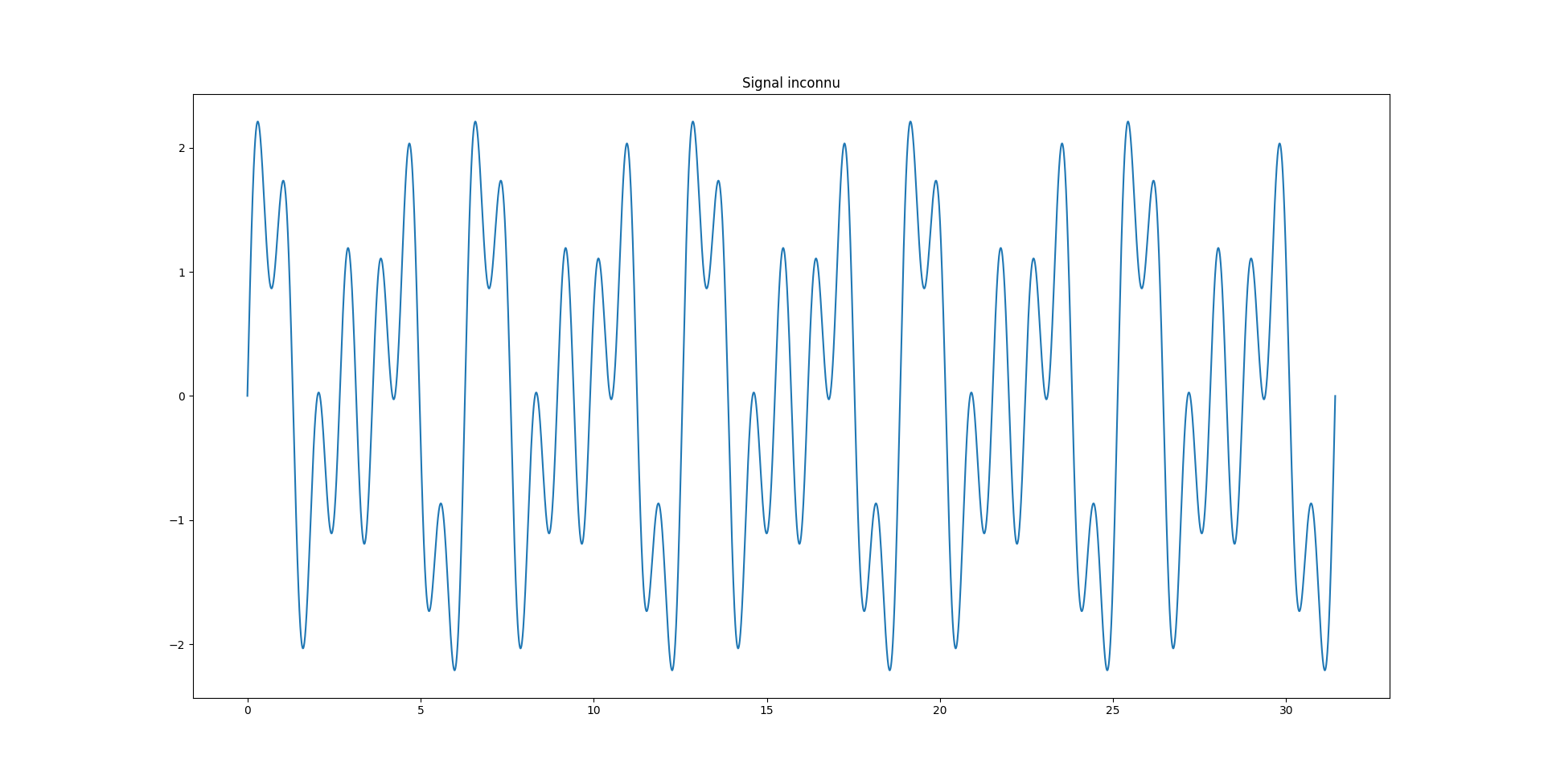
Comment pourrait-on essayer de déterminer de quoi est composé ce signal ? Une manière de procéder consisterait à chercher quels fonctions élémentaires (sinusoïdes) sont les plus susceptibles de reconstruire fidèlement ce signal. On pourrait essayer rapidement à l’aveugle, mais on se retrouverait rapidement vite face à un mur:
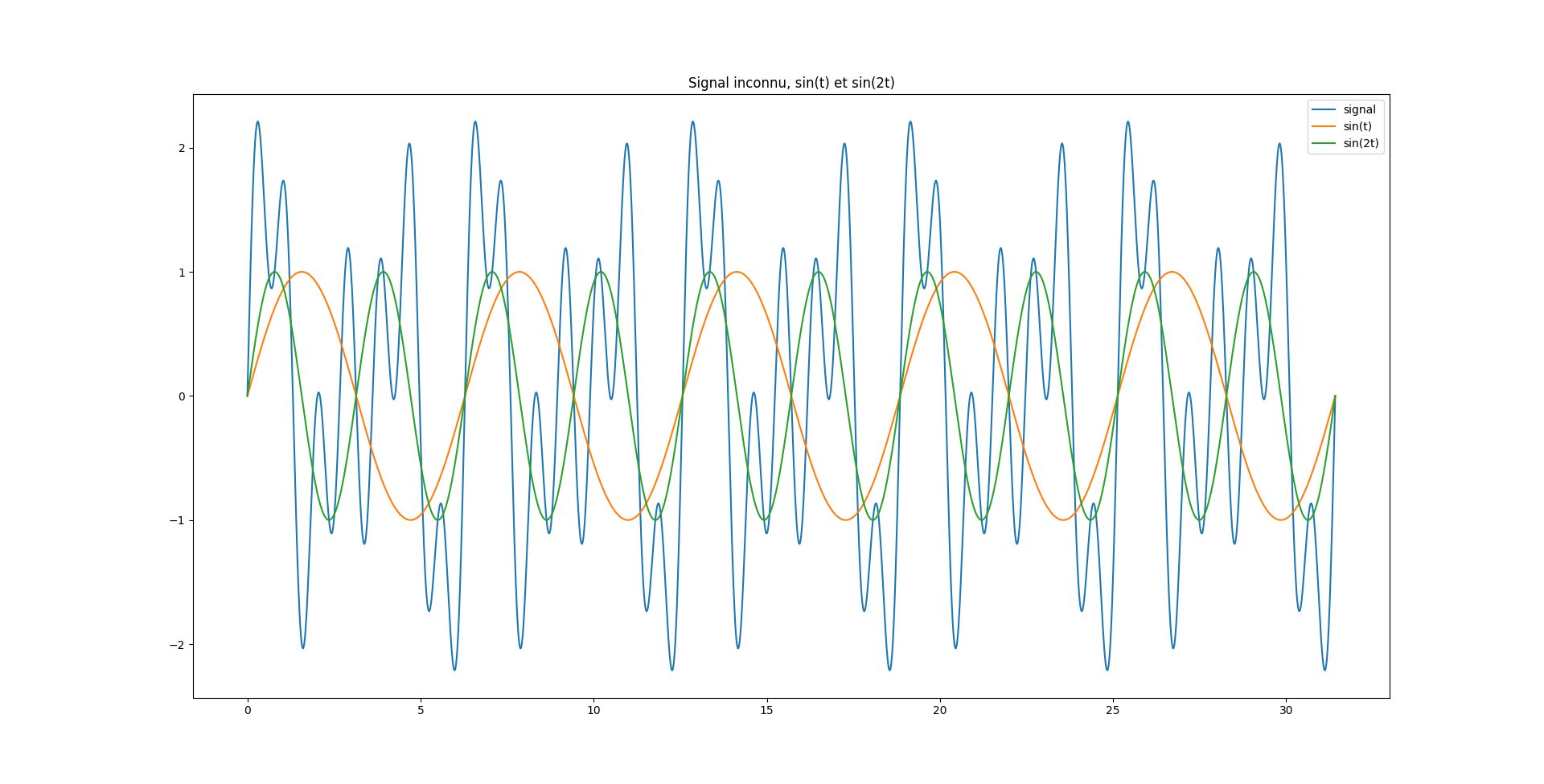
Comment déterminer si notre signal est davantage similaire à \(\sin(t)\) que \(\sin(2t)\), ou l'inverse ?
Une manière de procéder consisterait à calculer la corrélation de notre signal et de notre sinusoïde:
$$ corr(X, Y) = \frac{cov(X, Y)}{\sigma_{X}\sigma_{Y}} = \frac{E[(X - \mu_{X}) * (Y - \mu_{Y})]}{\sigma_{X}\sigma_{Y}} $$En pratique, on peut simplifier beaucoup cette expression:
- La moyenne des sinusoïdes est nulle (\( \mu_{X} = 0 \)).
- L’écart type des sinusoïdes est fixe (\( \sigma_{X} = \frac{\sqrt{2}}{{2}} = 0.7071... \)).
- La moyenne du signal (ou l’écart type) restera la même, pour tous les sinusoïdes que l’on voudrait tester.
- L’espérance sera toujours divisée par le même facteur (la durée du signal).
On pourrait résumer cette vraisemblance à sa plus simple expression:
$$ \sum X * Y $$En appliquant une vue plus analytique, on aurait une expression de ce type:
$$ \int \text{signal}(t) \sin(\omega t) dt $$Une autre manière de calculer la vraisemblance serait d’employer (la racine de) l’erreur quadratique moyenne (communément notée (R)MSE), on se retrouverait avec une expression de ce type:
$$ \int (\text{signal}(t) - \sin(\omega t))^{2} dt $$On développe le carré, on applique l’identité: \(\sin(\omega t)^2 = \frac{1}{2} - \frac{1}{2}\cos(2 \omega t)\), et l'on obtient:
$$ \int \text{signal}(t)^2 - 2 \text{signal}(t) \sin(\omega t) + \frac{1}{2} - \frac{1}{2} \cos(2 \omega t) dt $$On obtient 4 intégrales, dont seul le deuxième terme a de l'importance. En effet, soit les intégrales ne font pas intervenir notre sinusoïdes et sont donc communes à toutes (1 et 3), soit l'intégrale de \(\cos(\omega t)\) est bornée par \(| \frac{2}{\omega} |\) (4). Remarquons l'apparition du signe moins, comme nous cherchons à minimiser l'erreur, alors qu'avant, on voulait maximiser la corrélation.
Convolution
La convolution (ou produit de convolutions) est une manière de combiner deux signaux afin d’en former un troisième.
Traditionnellement, on définit le produit de convolution comme suit :
$$ (f \star g)(x) = \int_{-\infty}^{\infty} f(t) g(x - t) dt $$Cela est très barbare mais généralise le concept de moyenne glissante. Pour chaque point du nouveau signal en \(x\) (la variable indépendante), on va calculer l’intégrale du produit de deux fonctions dont l’une a été retournée et déplacée (la partie \(x - t\), le shift).
La première observation que nous pouvons effectuer est que \(x\) définit le décalage de la fonction \(g(.)\). Mais on garde bien partout le même \(g(.)\), on déplace le graphique dans le sens gauche-droite. La seconde est que \(g(.)\) a été retournée, on a \(g(x - t)\) et non \(g(t - x)\). D'une part, \(g(t - x)\) est appelée corrélation et non convolution, d'autre part, c'est pour introduire une notion de causalité (en fonction du temps traditionnellement) et enfin afin que le domaine temporel corresponde au conjugué complexe dans le domaine des fréquences (mais nous reviendrons sur ce point).
Cette opération de convolution s’articule vraiment en trois grande étapes:
- On fait shifter notre fonction \(g(.)\).
- On prend le produit de \(f(.)\) et \(g(.)\).
- On calcule l’intégrale de ce produit.
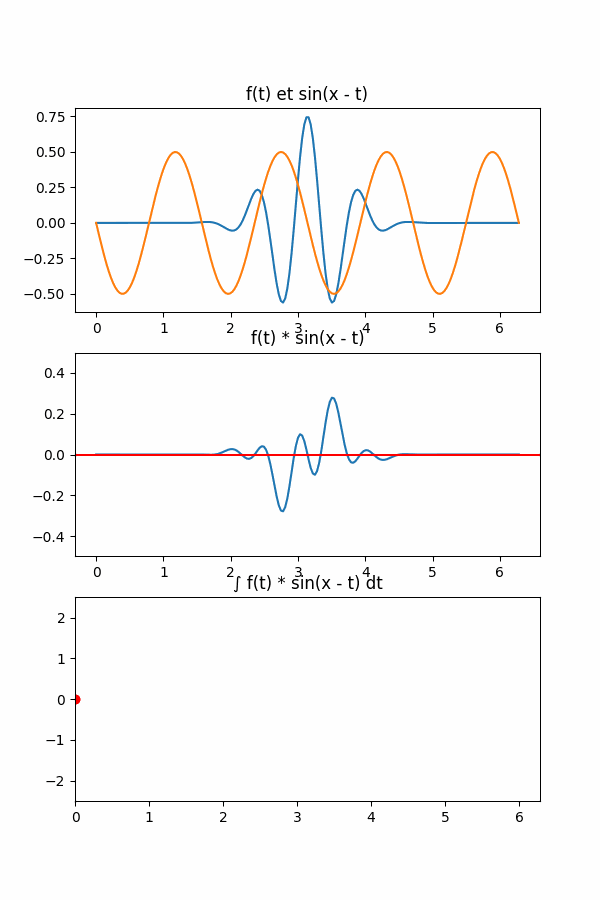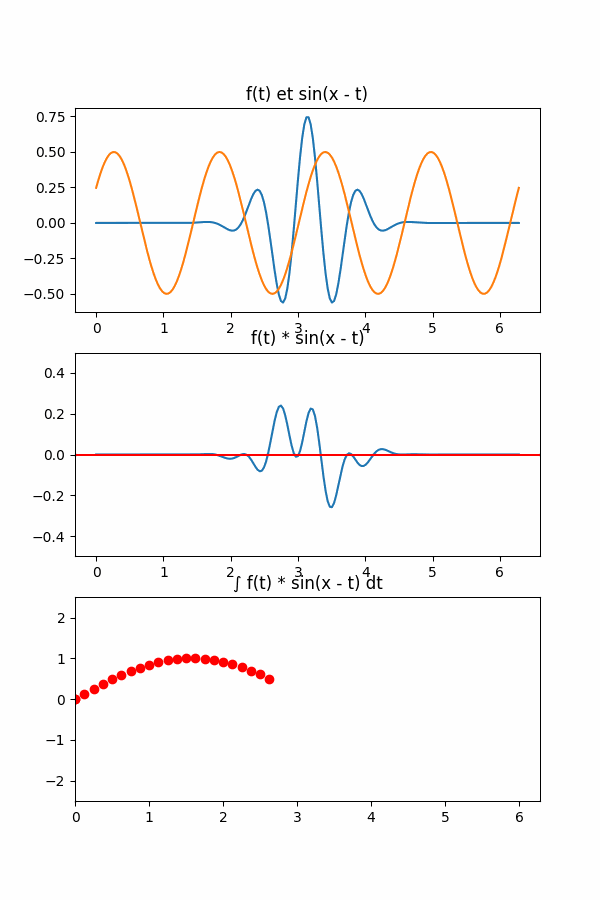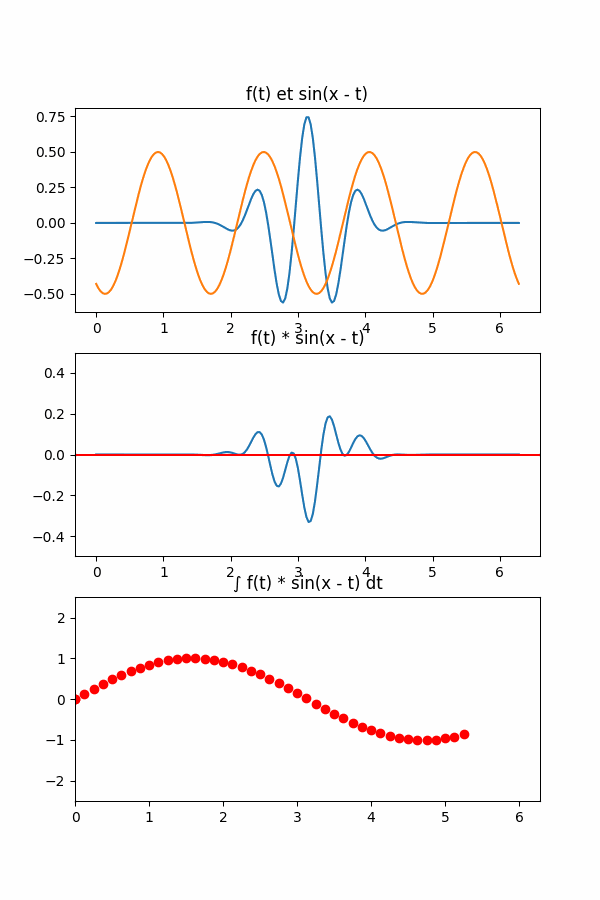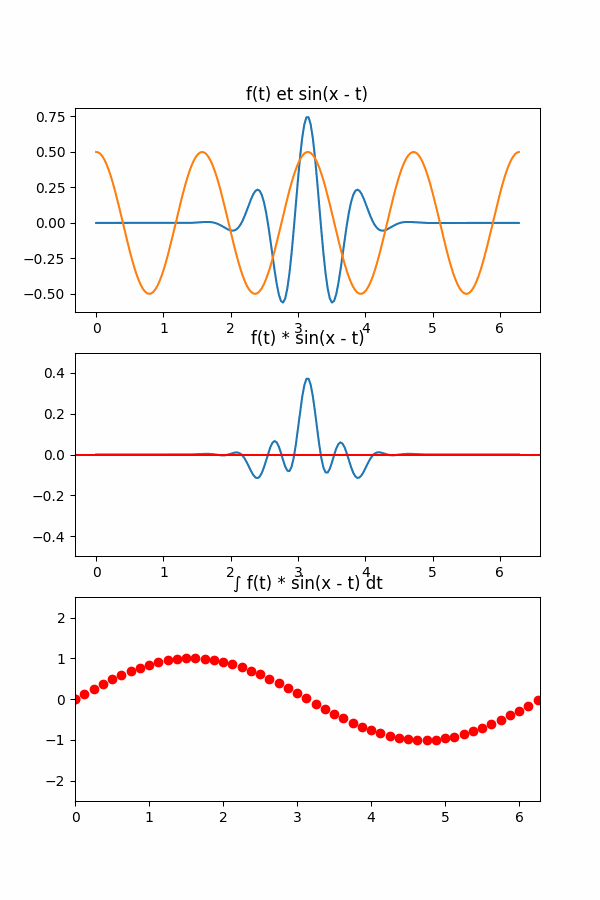
Et bien la convolution consiste à faire varier ce \(g(.)\) afin de regarder les résultats dans le domaine des fréquences et ainsi repérer lesquelles avaient la plus grande intégrale. Sur notre, exemple, on aurait le schéma suivant:
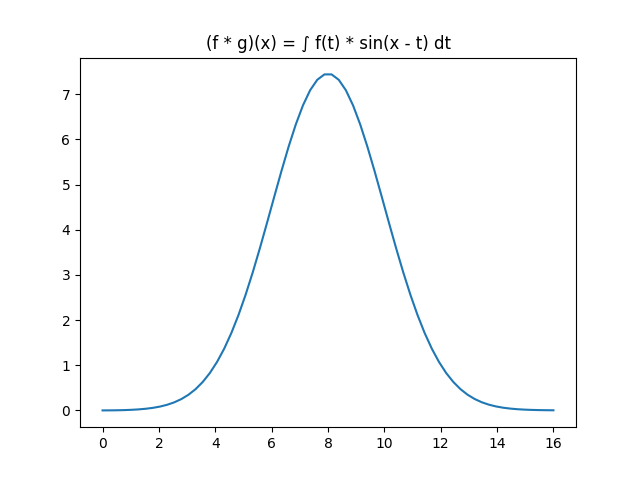
Transformée de Fourier
La transformée de Fourier est définie comme suit:
$$ \hat{f}(\xi) = \int_{-\infty}^{\infty} f(t) e^ {-i 2 \pi \xi t} dt $$On retrouve une construction similaire au produit de convolution.
Cependant où est donc passé le shift dans cette expression ? L’astuce réside dans le fait que \(e^{i}\) représente la formule d'Euler: \(e^{i} = \cos(x) + i \sin(x)\) et lorsque l’on additionne deux sinusoïdes, on obtient une sinusoïde de même fréquence mais avec un déphasage qui peut être contrôlé avec l’amplitude de ces dernières. La conséquence est que la transformée de Fourier donne plus que l’information sur la fréquence, elle donne également la phase pour laquelle le signal est maximisé.
On peut faire remarquer que la partie cosinus (fonction paire) donne donc les mêmes résultats pour \(t\) et \(-t\). Au contraire, la partie sinus (fonction impaire) donnera une valeur différente. En particulier, les valeurs en \(-t\) donnent l’amplitude des cosinus et sinus tels que leur addition (pour une même fréquence) donne une sinusoïde, qui lors de la convolution, donne la valeur maximale pour la fréquence. Mieux que cela, sur base de ces deux nombres, on peut calculer tant leur magnitude1 (qui donne leur contribution au signal) que leur phase en prenant l’arc tangent (atan2(x, y)).
- On distingue l’amplitude de la magnitude parce que l’amplitude sous-entend le sens de la relation alors que la magnitude reprend uniquement la valeur absolue.↩
Transformée de Fourier discrète
La transformée de Fourier est très pratique et trouve des usages dans de très nombreux domaines des sciences. Seulement, lorsque l’on cherche à l’appliquer au monde réel, on est vite confronté aux difficultés de travailler avec l’infini.
On préfère alors travailler avec la transformée de Fourier discrète. Au lieu de travailler sur une variable continue et tester une infinité de sinusoïdes, on ne va travailler qu’avec un nombre fini de sinusoïdes et de valeurs pour la fonction étudiée. Pour cela, on se base tant sur la fréquence d’échantillonnage \(R\) du signal que sur la taille de l’échantillonnage \(N\).
$$ X_{k} = \sum_{n=0}^{N-1} x_{n} e^{-i 2 \pi \frac{k}{N}n} $$Cette discrétisation apporte de nombreux phénomènes. En effet, entre deux points d’échantillonnage, le signal pourrait faire ce qu’il a envie. En particulier, au-delà de la fréquence de Nyquist (Nyquist rate), qui est définie comme la moitié de la fréquence d’échantillonnage, les fréquences des sinusoïdes vont présenter une "même vue" des données échantillonnées, on dit qu’elles sont réfléchies dans la moitié inférieure du spectre des fréquences. Ce phénomène s’appelle le repliement de spectre ou aliasing.
Dans les faits, les signaux de hautes fréquences seront interprétés de la même manière que ceux de basses fréquences. Pour contrer cela, il suffit d’échantillonner à au moins 2 fois la fréquence la plus élevée du signal (typiquement 44.100 Hz pour l’audio puisque nous n’entendons pas au delà de 20.000 Hz).
Maintenant, prenons la transformée discrète d’un signal quelconque:
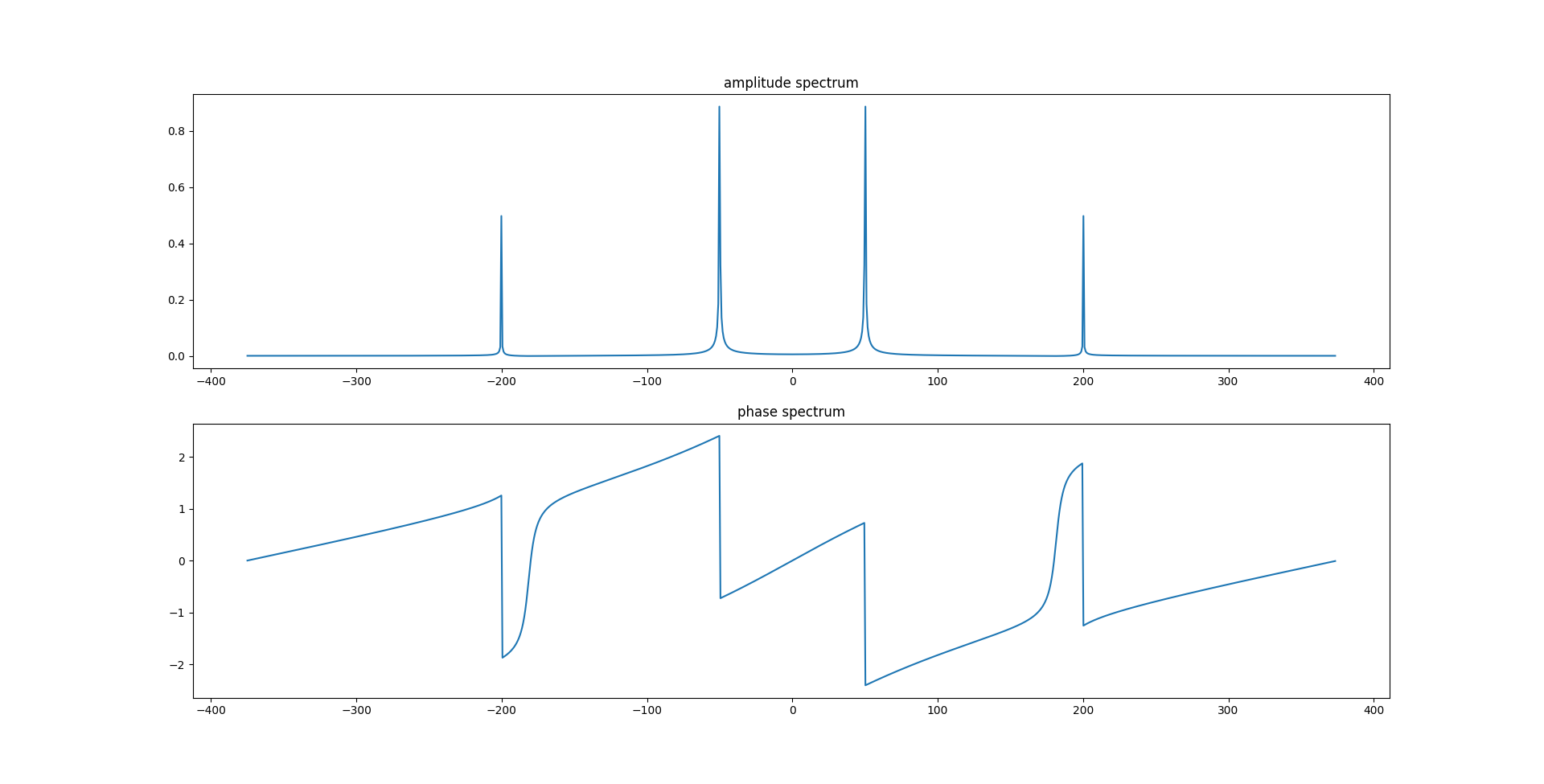
On observe qu’il existe une symétrie axiale pour les amplitudes et une symétrie centrale pour les phases. C’est le cas parce que j’ai employé un signal réel (au sens littéral, qui est non-complexe) et de fait, si on applique la transformée inverse, la sommes parties imaginaires s’annulerait. Mais c'est plus que ça. Vous remarquerez que l'axe des abscisses contient des fréquences négatives ! Cela s'explique par le fait que \(e^{ix}\) forme une spirale sur le plan complexe (lorsqu'on fait évoluer \(x\)) et que celle-ci peut tourner dans deux sens. Mais il peut également y a également des conséquences concrètes à ces parties imaginaires telles que le chevauchement de bandes de fréquence des radios.
Fast Fourier Transform (FFT)
L’algorithme employé pour calculer une transformée de Fourier discrète s’appelle la transformée rapide de Fourier ou Fast Fourier Transform (FFT). Cet algorithme est optimal en complexité \(O(n \log n)\) et fournit toutes les informations dont nous avons besoins. Si vous cherchez plus d’information sur ce sujet, il existe un tutoriel très complet de klafyvel: sur ce sujet.
FFT prend en entrée le signal (éventuellement complexe) et produit une liste de N nombres complexes qui sont l’ensemble des sinusoïdes nécessaires pour reproduire le signal d’entrée. Cela va de l’entrée 0 associée à la fréquence 0, à N - 1 l’avant dernière fréquence avant celle d’échantillonnage. De manière plus générale:
$$ f_{k} = \frac{k}{N} * R $$La transformée rapide de Fourier (FFT) requiert que la longueur du signal traité soit une puissance de 2. Or, en pratique, cela n’arrive jamais. Il suffirait donc de découper son signal en plein de petits intervalles (frame) qui possèdent une taille plus adéquate. Seulement, comme on coupe le signal un peu n’importe où, on risque d’avoir des effets de bords. En particulier, FFT risque de faire apparaître des signaux de haute fréquence dans le signal (alors qu’ils n’existent pas et sont purement induits par notre découpage).
Il y a plusieurs idées qui peuvent émerger afin de résoudre ce problème:
- Zero-Padding ;
- Overlapping ;
- Time domain interpolation / resampling ;
- Zero-crossing detection ;
- Signal decomposition ;
- etc … ;
Mais le plus classique est d’employer des fonctions de fenêtrages (windowing functions) telles que Hamming, Hann, Bartlett, Blackman, Tukey, … Chacune d’entre elle présente certains avantages et inconvénients qu’il est nécesaire de s’approprier avant d’effectuer son choix. Les fonctions de fenêtrages permettent de s’assurer que les signaux (commencent et) se terminent par des valeurs quasiment nulles et donc que l’on se retrouve dans le cas standard.
Conclusions
Nous avons vu que la transformée de Fourier transforme le signal en un ensemble de sinusoïdes. Mais peut-on imaginer d’autres variantes ? Par exemple, Laplace a introduit une transformée à base de sinusoïdes décroissantes. Mais il existe de très nombreuses autres.
Une autre très grande famille de transformations module cette transition du domaine temporel vers le domaine des fréquences. Imaginons un feu de circulation routière, si on applique une transformée de Fourier dessus dans le domaine des couleurs, nous obtiendrons trois pics, un pour le rouge, un pour le vert et un pour l’orange. Mais, cela ne nous dit rien, ni sur leur ordre, ni sur leur durée. Pire que cela, si les trois feux étaient allumés en même temps, on aurait toujours le même résultat !
Pour prendre en compte cet aspect, on emploie encore régulièrement la décomposition en ondelettes (wavelets) qui sont une très vaste famille de fonctions qui peuvent être vues comme une perturbation de faible durée. Toute l’astuce réside dans le fait qu’elles soient apériodiques et possèdent de bonnes caractéristiques (intégrale nulle, de carrées intégrables, …). On obtient d’autres types de représentations puisqu’on possède deux variables (temps et fréquence). Mais cela nous permet d’analyser cet arbitrage qui existe entre ces deux domaines.
La chaîne de @3blue1brown propose une autre interprétation de la transformée de Fourier et explore davantage cette relation duale, d'arbitrage entre le domaine temporel et des fréquences.