En mathématique, comme dans toute autre discipline, il est bon d'avoir une certaine intuition des situations rencontrées. Toutefois il faut rester conscient qu'une intuition n'est jamais une preuve.

A titre d'exemple, nous mentionnerons deux "curiosités" qui nous feront réfléchir quant à la qualité de notre intuition.

Tout d'abord la longueur d'une courbe. Chacun sait qu' Archimède a calculé avec grande précision la longueur de la circonférence en utilisant les polygones inscrits et circonscrits. Il est "évident" que le périmètre d'un polygone inscrit est inférieur à la circonférence et que lorsque le nombre de côtés du polygone augmente indéfiniment, le périmètre tend vers la circonférence.

Voici un exemple où l'on considère un segment de droite. Sur ce segment pris comme hypoténuse, on construit un triangle rectangle. Si le segment a pour longueur \(l\), la somme des longueurs des deux autres côtés vaudra \(l\sqrt{2}\). 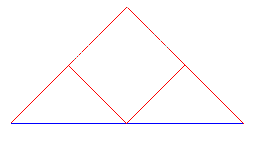Subdivisons à présent en deux chacun des côtés du triangle, et joignons le milieu de l'hypoténuse aux milieux des côtés de l'angle droit. La somme des longueurs des 4 segments inclinés à 45° sur l'hypoténuse reste constante (et vaut \(l \sqrt {2}\)). En répétant l'opération, on obtient une courbe en "zigzag" formée de 8 segments, de 16 segments,... qui tend manifestement vers le segment de droite.

Et pourtant! La longueur de cette courbe en "zigzag" reste constante et égale à \(l\sqrt {2}\).

Que se passe-t-il? Tout simplement ce zigzag ne tend pas "convenablement" vers le segment de droite. Si nous regardons la tangente en un point d'abscisse fixée, nous voyons qu'elle est inclinée à 45° vers la droite ou vers la gauche, mais qu'elle ne tend pas à devenir horizontale.

Montrons à présent une autre courbe "paradoxale". Soit un triangle équilatéral de coté \(c\). Son périmètre vaut \(3 c\). 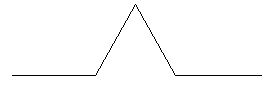Décidons à présent de modifier cette courbe de la manière suivante. Nous remplaçons tout segment par la figure formée de 4 petits segments et pour qu'il n'y ait pas d'ambiguïté nous dirigerons la pointe vers l'extérieur.

A la première étape nous obtenons une étoile de David. Si nous en calculons le périmètre, il suffira de partir du périmètre de la courbe initiale (le triangle équilatéral) et de remarquer que chaque segment a été remplacé par une figure dont la longueur en vaut les 4/3. Le périmètre de l'étoile vaudra donc \(4 c\). En recommençant, nous obtenons une courbe formée de 12 x 4 segments dont le périmètre vaudra \(16 c/3\).

En répétant indéfiniment l'opération, ce polygone tend vers une courbe dont la longueur aura, à chaque étape, été multipliée par 4/3, donc une courbe de longueur infinie.

Et pourtant ! Cette courbe, due au mathématicien von Koch, reste entièrement comprise à l'intérieur d'un cercle. Voila donc un domaine d'aire finie limité par une courbe de longueur infinie.