Dans cet article, on va s'intéresser au problème de la route et de la roue. L'idée est de se demander quelle est la route "parfaite" pour un certain type de roue et, inversément, quelle est la roue la plus adaptée à une certaine route ?

Mais, pour commencer, quel est le critère qui permet de déterminer si une roue est la mieux adaptée ? On souhaite que le transport s'effectue avec le minimum d'accrocs possibles, qu'on ne se fasse pas secouer dans tous les sens. Pour cela, il faut que l'essieu reste le plus plan possible; que l'axe de rotation de la roue se déplace selon une horizontale.

Il existe deux grandes propriétés à observer lorsqu'une roue se déplace:

1. Le point de contact de la route avec la roue et l'essieu forme une ligne verticale et perpendiculaire à la route.
2. La vitesse de ce point de contact est nulle. Sinon, la roue glisserait sur la route.

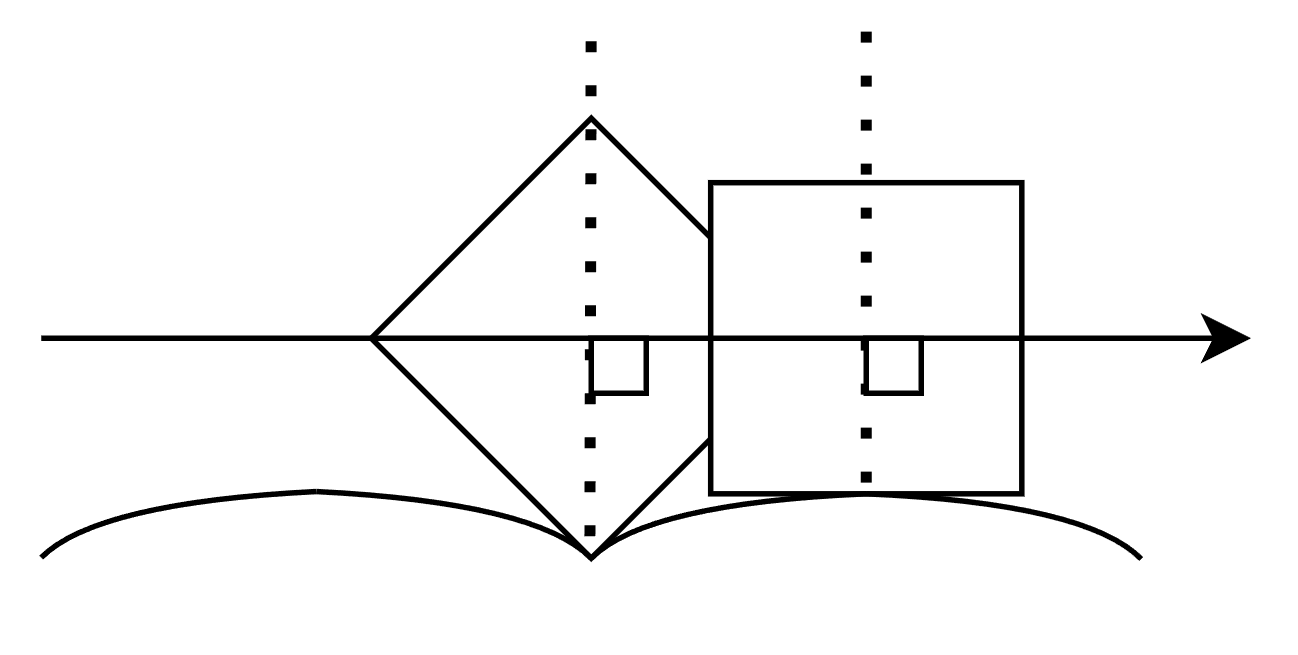
Une fois que ces deux propriétés sont bien assimilées, on peut décrire nos équations générales tant pour la route que pour la roue:

La route aura une équation paramétrique classique:

$$ \begin{cases} x = x(t) \\ y = y(t) \end{cases} $$

tandis que la roue sera exprimée dans des coordonnées polaires (puisqu'elle roule, ce sera plus pratique) avec \(r\) pour "rayon" (attention que ce n'est pas forcément un cercle) et \(\theta\) pour angle:

$$ \begin{cases} r = r(t) \\ \theta = \theta(t) \end{cases} $$

Notre repère sera déterminé par la position de l'essieu avec l'axe horizontal de déplacement et l'axe vertical conditionné par l'orthogonalité.

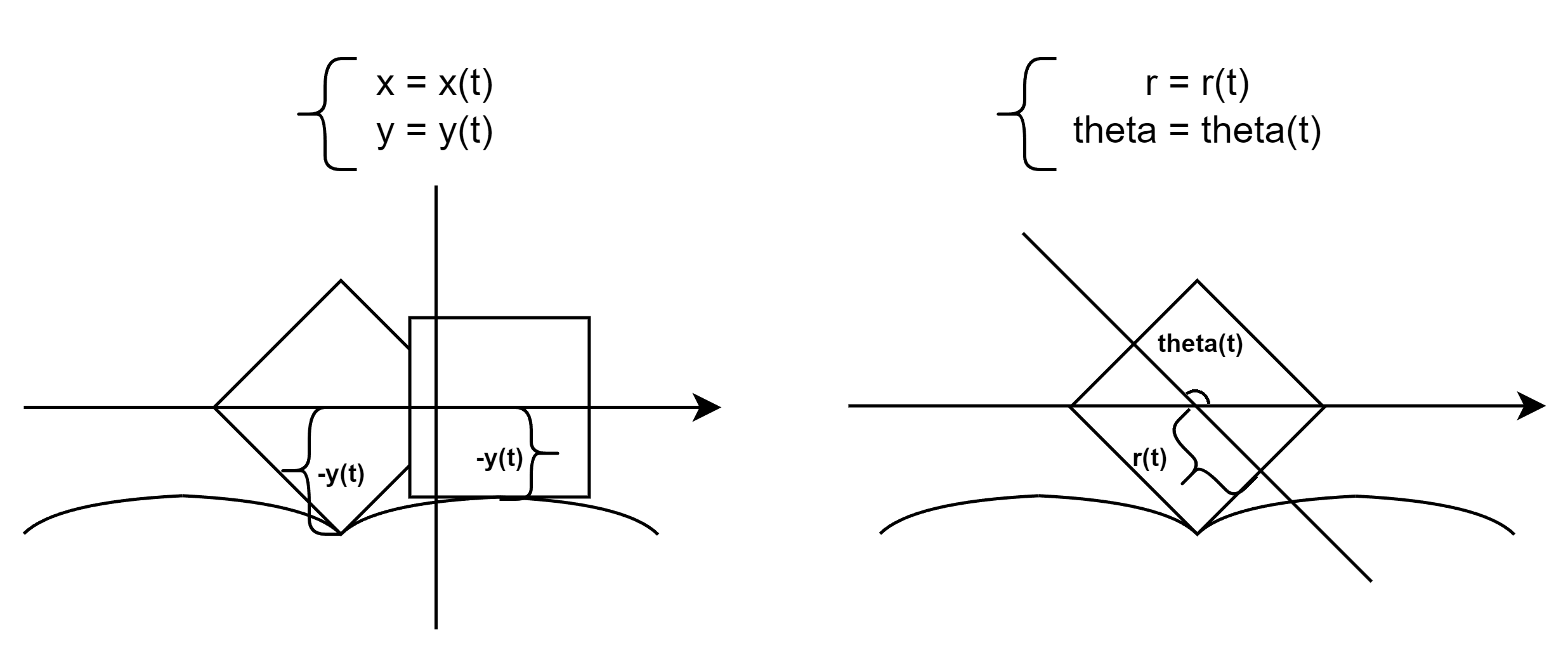
À ces équations très générales, on peut insérer nos conditions du système:

1. Nous savons que la route est située sous la roue. On a que: \(y = y(t) < 0\).
2. On s'assure que le même \(t\) soit employé dans les équations de telle sorte que le même point de contact soit décrit entre les deux surfaces.

Maintenant, comment faire en sorte que les deux systèmes de coordonnées cohabitent, qu'on puisse exprimer les coordonnées de l'un en fonction de l'autre ?

Premièrement, si la distance entre l'axe horizontal et la route vaut \(-y(t)\), dans le repère de la roue, ce point de contact est situé à \(r(t)\).

$$ -y(t) = r(t) $$

Pour trouver \(x(t)\) en fonction de \(r(t)\) et \(\theta(t)\), il faut se baser sur l'observation que le point de contact possède une vitesse nulle. Or, si celui est "stationnaire" dans le repère de la route, il se déplace dans le repère de la roue. Et, en particulier, que les vitesses relatives dans les deux repères se compensent.

La vitesse dans le repère de la route s'exprime comme la dérivée de la position en \(x\):

$$ \frac{dx}{dt} $$

Tandis que, dans le repère polaire de la roue, la vitesse est définie comme:

$$ r \frac{d\theta}{dt} $$

Nos équations de correspondance entre les deux repères s'écrivent donc:

$$ \begin{cases} y = -r \\ \frac{dx}{dt} = r \frac{d\theta}{dt} \end{cases} $$

Comme exemple, on peut essayer de voir ce que cela donne pour un carré. Malheureusement, paramétriser un carré dans quelque coordonnée est quelque peu compliqué ... On peut réduire le problème à la paramétrisation de juste un des côtés du carré. Pour l'exemple, on prendra un carré de côté 2, centré à l'origine.

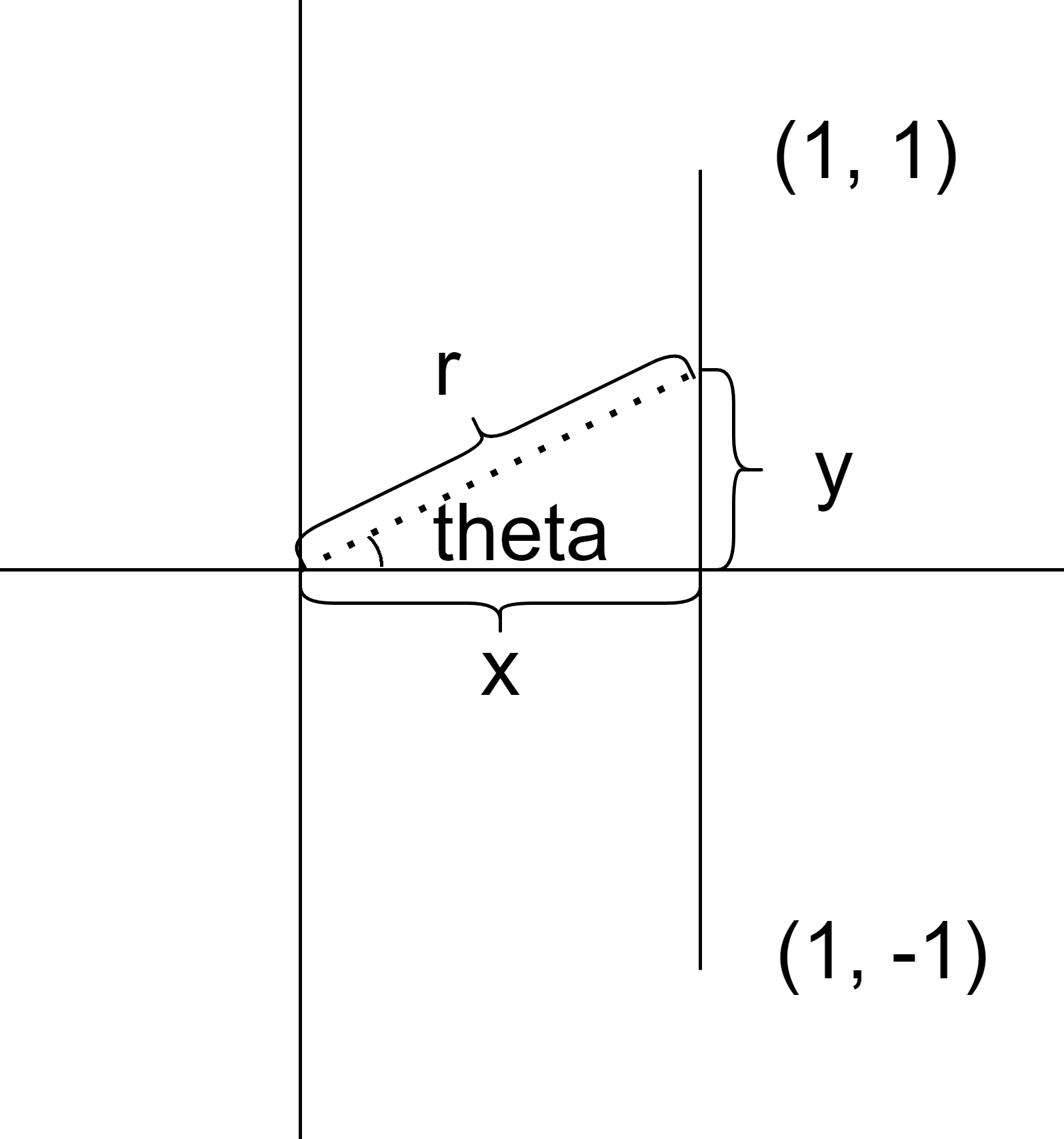
D'un côté, on aura:

$$ \begin{cases} x_{roue}(t) = 1 \\ y_{roue}(t) = t \end{cases} $$

et de l'autre, en appliquant la transformation des coordonnées polaires en cartésiennes (puisqu'on décrit ici la même courbe):

$$ \begin{cases} r_{roue}(t) = \sqrt{x^ {2}_{roue}(t) + y^ {2}_{roue}(t)} = \sqrt{1 + t^{2}} \\ \theta_{roue}(t) = \arctan(\frac{y_{roue}(t)}{x_{roue}(t)}) = \arctan(t) \end{cases} $$

Il ne reste plus qu'à appliquer nos équations dans notre système afin de trouver l'équation de notre route:

$$ \begin{cases} y = -r = -\sqrt{1 + t^{2}} \\ \frac{dx}{dt} = r \frac{d\theta}{dt} = \sqrt{1 + t^{2}} \frac{1}{1 + t^{2}} = \frac{1}{ \sqrt{1 + t^{2}}} \end{cases} $$

Il ne reste plus qu'à intégrer pour obtenir \(x(t)\):

$$ x(t) = \int \frac{1}{ \sqrt{1 + t^{2}}} dt = \sinh^{-1}(t) $$

Et voilà:

$$ \begin{cases} x(t) = \sinh^{-1}(t) \\ y(t) = -\sqrt{1 + t^{2}} \end{cases} $$

Entre nous, exprimé en forme paramétrique, ces équations ne nous parlent pas vraiment. On peut convertir en forme cartésienne:

$$ \begin{cases} x(t) = \sinh^{-1}(t) \iff t = \sinh (x) \\ y(t) = -\sqrt{1 + t^{2}} = -\sqrt{1 + \sinh (x)} = -\cosh (x) \end{cases} $$

Et on tombe sur une chaînette (catenary curve), la courbe que l'on obtient lorsque l'on fait tomber une chaînette en la tenant par deux bouts.

La route devra donc être composée d'un ensemble de chaînettes qui se répètent à l'infini pour permettre un trajet agréable avec une roue carrée.

Pour trouver la roue parfaite associée à une roue, il faut exprimer nos équations de conversions:

$$ \begin{cases} y = -r \\ \frac{dx}{dt} = r \frac{d\theta}{dt} \end{cases} $$

afin d'isoler \(r\) et \(\theta\):

$$ \begin{cases} r = -y \\ \frac{dx}{dt} = r \frac{d\theta}{dt} \iff \frac{d\theta}{dt} = \frac{1}{r} \frac{dx}{dt} = -\frac{1}{y} \frac{dx}{dt} \end{cases} $$

Malheureusement, si on emploie les équations telles quelles, on obtient un gros problème. Le résultat n'est pas forcément une belle forme convexe.

Il faut imposer que la rotation de la roue par rapport à la route s'effectue sur une rotation complète (\(2\pi\)) ou une fraction du cercle (\(2\frac{\pi}{k}\)). En d'autres termes, on veut que la route se répète autant que nécessaire afin que la roue finisse son cycle. Autrement dit, que pour une période \(T\):

$$ \int^{t_{0} + T}_{t_{0}} \frac{d\theta}{dt} dt = 2 \frac{\pi}{k} $$

où, dans notre équation de conversion:

$$ \int^{t_{0} + T}_{t_{0}} -\frac{1}{y} \frac{dx}{dt} dt = 2 \frac{\pi}{k} $$

Ce qui est embêtant avec cette propriété, c'est qu'il existe une infinité de solution en fonction de \(k\). En réalité, ce problème est lié à une liberté sur la "hauteur" de la courbe \(y(t)\). Plus la courbe sera éloignée de l'origine, moins la roue parcourra de distance avant de retomber sur une répétition de la route.

Si on prend du recul sur le problème. On peut le formuler d'une autre manière. Est-il possible de décrire une roue qui tourne de manière agréable autour d'une autre roue ?

On observe qu'il existe un segment de droite passant par les deux centres de nos "roues" et qui est perpendiculaire à leur point de contact. Si on pose que le rayon que parcourt la roue externe vaut 1, alors on a que:

$$ \rho(t) + r(t) = 1 $$

Pour la vitesse, on a la vitesse tangentielle qui est égale (mais avec un signe moins puisque les roues tourneront dans des sens opposés).

$$ \rho(t) \frac{d\phi}{dt} = - r(t) \frac{d\theta}{dt} $$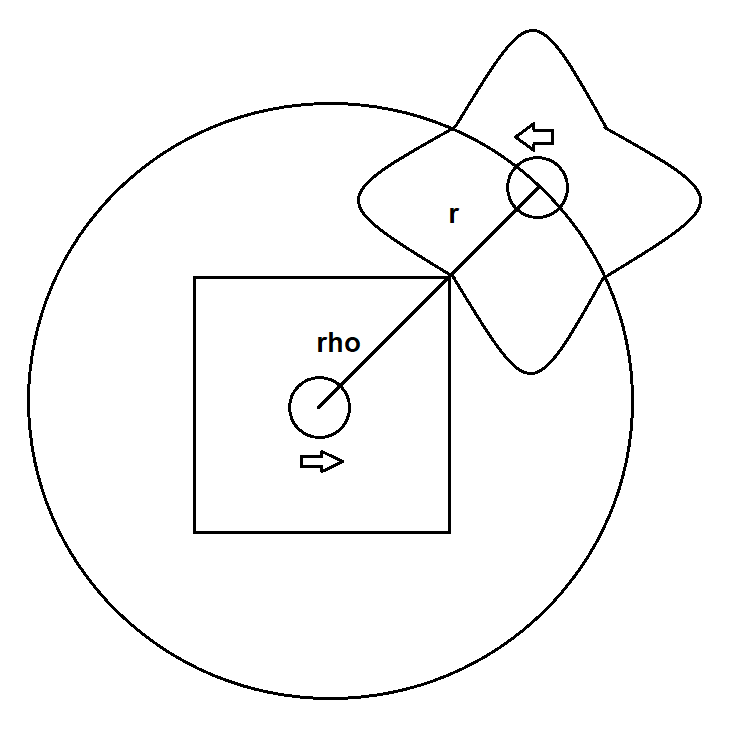

Au final,

$$ \begin{cases} \rho(t) + r(t) = 1 \\ \rho(t) \frac{d\phi}{dt} = - r(t) \frac{d\theta}{dt} \end{cases} $$

Si on prend, pour exemple, un cercle avec pour rayon: \(r(t) = 1/4\) et \(\theta(t) = t\), on a:

$$ \begin{cases} \rho(t) + \frac{1}{4} = 1 \iff \rho(t) = \frac{3}{4} \\ \rho(t) \frac{d\phi}{dt} = - r(t) \frac{d\theta}{dt} \iff \frac{3}{4} \frac{d\phi}{dt} = - \frac{1}{4} \frac{d~ t}{dt} \iff \frac{d\phi}{dt} = -\frac{1}{3} \iff \phi(t) = -\frac{1}{3} t \end{cases} $$

Assez naturellement, on se rend compte que si la roue est 3 fois plus grande, alors elle doit rouler 3 fois plus lentement pour arriver à la même position.