Le calcul des dérivées de fonctions algébriques ne présente guère de difficultés. Quand on rencontre la forme 0/0, cela résulte tout simplement du fait que numérateur et dénominateur ont un facteur commun. Il suffit alors de simplifier par celui-ci. Il n'en est pas de même lorsqu'on étudie d'autres fonctions (goniométriques, exponentielles, ...).

Le premier exemple se présente lors de la recherche de la dérivée de la fonction \(\mathbf{sin~}x\). On est confronté à la détermination de la valeur d'une forme 0/0 provenant de \(\mathbf{sin~}x /x \) qui doit être calculée pour \(x = 0\). C'est, en fait, un des premiers contacts avec l'analyse. Une introduction à la notion de limite et de ses règles de calcul s'impose.

Lorsque l'on parcourt des forums (francophones), on reste ahuri en voyant les commentaires relatifs à la limite de \(\mathbf{sin~}x /x \) lorsque \(x\) tend vers 0. Peut-être en a-t-on oublié la démonstration ? C'est pardonnable, d'autant plus, que par la suite, on ne parle plus jamais de cette fameuse limite. Par contre, ce qui est plus grave, c'est d'avoir oublié qu'il a été indispensable de calculer sa valeur afin de pouvoir établir les dérivées des fonctions goniométriques ; de plus, on a utilisé une hypothèse bien précise : l'angle \(x\) doit être exprimé en radians ! On peut lire :

"C'est évident : il te suffit d'appliquer la règle de l'Hospital"

"Utilise le développement en série de MacLaurin et simplifie"...

Serait-ce aussi simple ? Mauvaises réponses, cercles vicieux ; elles demandent toutes la connaissance de la dérivée de \(\mathbf{sin~}x\) !

Une réponse, plus "moderne", un rien meilleure, propose l'utilisation d'une calculette : on prend x très petit (0,1 0,01 ou 0,001... mais également -0,1 -0,01 ou -0,001...) et on constate que la valeur de \(\mathbf{sin} x /x \) se rapproche plus en plus de la valeur 1. Mais seul un expérimentateur se contenterait d'une telle réponse !

Au passage, signalons que, pour arriver à ce résultat, il faudra avoir choisi sur sa calculette le radian pour unité de mesure des angles !

Certaines calculettes permettront même d'en avoir la "preuve" en affichant le graphique de cette fonction :

Mais un dessin n'a jamais constitué une preuve. Que faire avec cette fonction sinus ?

Rappelons-nous la définition du sinus d'un angle (ou de l'arc qui lui est associé). Tout se passe dans un cercle - d'orientation anti-horaire - dont le rayon est choisi pour unité de mesure : le cercle trigonométrique.

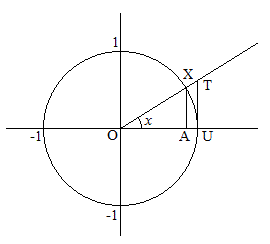
Le sinus de l'angle \(x\), ou de l'arc associé UX, est la mesure du segment AX. Autrement dit, le sinus de l'angle \(x\) est l'ordonnée du point X dans le repère donné. Ensuite on passe facilement à la définition des autres fonctions goniométriques : le cosinus de \(x\) est égal à l'abscisse OA du point X. Ensuite la tangente de l'angle \(x\) est le rapport de \(\mathbf{sin~}~x\) à \(\mathbf{cos~} x\) avec une belle interprétation géométrique, \(\mathbf{tan} x\) est l'ordonnée du point T de la tangente en U.

De là, on conclut rapidement que AX < UX < UT et, en exprimant les mesures de ces grandeurs en fonction de \(x\), on obtient : \(\mathbf{sin~}x\) <\(x\) < \(\mathbf{tan~}x\). On divise ces inégalités par \(\mathbf{sin~}x\) et on obtient avec \(x\) positif : \(1 < x/\mathbf{sin~} x < 1/\mathbf{cos~}x\). On constate alors que si \(x\)> tend vers 0, \(\mathbf{cos~}x\) tend vers 1 et \(x/\mathbf{sin~}x\) est "coincé" entre ces deux valeurs. Par conséquent, la limite de \(\mathbf{sin~} x /x \) vaut 1. C'est ce que nos amis français appellent, avec humour, le théorème des gendarmes ! Par prudence, on vérifie évidemment que tout va bien si \(x\) est négatif, et on achève, ainsi, la démonstration. Sauf que...

Il est simple de prouver que le segment AX est plus court que l'arc UX. En effet, l'arc UX est plus grand que le segment UX (le plus court chemin) et de plus une oblique UX issue de X est plus grande que la perpendiculaire AX. Par contre, il n'est pas évident que l'arc UX soit plus court que le segment UT. Bien sûr, cela se "voit", mais encore faudrait-il le démontrer.

Encore une démonstration insatisfaisante.

Nous serions peut-être plus convaincus en considérant les aires.

Le triangle OAX est plus petit que le secteur OXU qui est lui même plus petit que le triangle OTU. Exprimons ces aires : l'aire d'un triangle vaut la moitié du produit de la base par la hauteur. L'aire d'un cercle (d'angle au centre \(2\pi\)) vaut \(\pi R^2\). L'aire d'un secteur d'angle \(x\) vaut \((x/2\pi).\pi R^2\), ce qui dans le cas du cercle trigonométrique donne \(x/2\). On a donc : \((\mathbf{sin~}x.\mathbf{cos~} x)/2 < x/2 < (\mathbf{tan~}x )/2\). A présent il suffit de multiplier cette inégalité par 2 et de la diviser, comme plus haut, par sin x . Les gendarmes qui entourent la fonction x / sin x nous offrent la démonstration de la valeur de la limite cherchée.

Démonstration ? Vraiment ?

Nous avons raisonné sur une figure peut-être incorrecte. Bien pire, nous avons admis que l'aire d'un cercle de rayon \(R\) vaut \(\pi R^2\) mais ce résultat, bien connu depuis l'école primaire et même depuis plus de deux millénaires par Archimède, ne sera malheureusement établi "rigoureusement" en classe que plus tard à l'aide du calcul intégral, c'est-à-dire moyennant la connaissance des dérivées des fonctions goniométriques.

Le fameux cercle vicieux réapparaît car la dérivée de \(\mathbf{sin} x\) dépend de la limite de \(\mathbf{sin} x /x \) lorsque \(x\) tend vers 0.

Où trouve-t-on de la rigueur dans tout cela ? Nulle part, mais est-ce bien nécessaire d'être un "intégriste" de la rigueur ? Bien sûr que non ; il suffit d'être réaliste et de signaler que le résultat obtenu par la simple contemplation d'une figure ne constitue pas une démonstration, mais sera toutefois admis.

Ceci dit, que faut-il retenir de tout cela ?

Le résultat trouvé :

\[\lim_{x\to 0}\frac{\mathbf{sin} x}{x}\]

est obtenu sous la condition que \(x\) est exprimé en radians . Donc la conséquence en est que le calcul de la dérivée de \(\mathbf{sin} x\) qui vaut \(\mathbf{cos} x\) n'est valable que lorsque \(x\) est exprimé en radians. En conséquence, les valeurs obtenues pour les dérivées des autres fonctions goniométriques, ne seront valables que si \(x\) est exprimé en radians. Cela s'oublie d'autant plus vite que le calcul de cette fameuse limite n'apparaît pratiquement plus jamais par la suite !

On s'en rend pourtant compte lorsque l'on songe à l'interprétation géométrique de la dérivée en un point \(x\) : c'est la pente de la tangente au graphique de la fonction en ce point. Si \(x\) est exprimé en radians, la dérivée de la fonction \(\mathbf{sin} x\), qui est égale à \(\mathbf{cos} x\), vaudra 1 à l'origine, ce qui signifie que la tangente au graphique de la fonction \(\mathbf{sin} x\) sera inclinée à 45°, ainsi qu'on peut le constater sur le graphique ci-dessous.

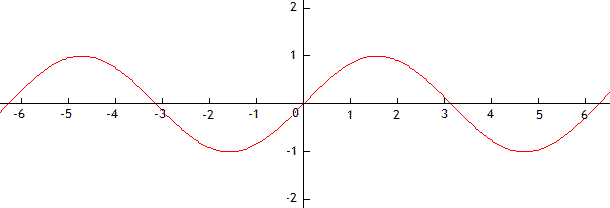
Au cas où la variable \(x\) est exprimée en d'autres unités, telles le degré ou le tour, il faudra tenir compte d'un facteur correctif.

A titre de comparaison voici le graphique de la fonction \(\mathbf{sin} x\) lorsque \(x\) est exprimé en nombre de tours.

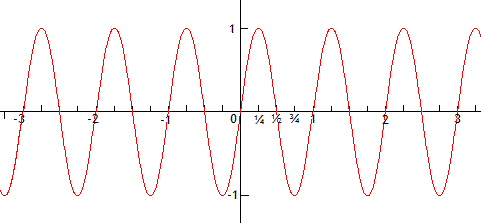
Il est clair que la dérivée à l'origine est différente de 1 ! Le facteur correctif vaut \(2\pi\). Dans ce cas la dérivée de \(\mathbf{sin} x\) vaut \(2\pi \mathbf{cos} x\).

Au cas où l'angle \(x\) est exprimé en degrés, le facteur correctif vaudrait \(\pi/180 (= 2\pi/360)\).

La simplicité des dérivées des fonctions goniométriques justifie enfin le choix, curieux aux yeux des non-mathématiciens, du radian comme unité de mesure des angles. À ce propos, signalons qu'une situation analogue se produira un peu plus tard lors de l'étude des dérivées des fonctions exponentielles et logarithmiques. On verra comment le choix d'un nombre bizarre : le nombre \(e\) (=2,718...) pour base de logarithmes, simplifiera à nouveau toutes les formules de dérivation.