Chacun connaît l'anecdote :

L'instituteur, ayant besoin d'un peu de répit, demande aux enfants de faire la somme des nombre de 1 à 100. Hélas ! Quelques secondes plus tard, le petit Carl Friedrich lève le doigt et dit j'ai terminé : la somme vaut 5050. Pas de chance pour l'instit ; le petit Gauss était déjà très doué...

Comment avait-il fait ? Tout simplement il avait remarqué que 1 + 100 égalait 2 + 99, 3 + 98...et ainsi de suite jusqu'à 50 + 51. Donc la somme égalait 50 fois 101, c'est-à-dire 5050.

Une jolie interprétation géométrique est la suivante :

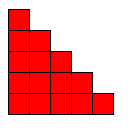Pour simplifier prenons la somme des nombres de 1 à 5. Chaque nombre est représenté par des carrés (d'aire 1) ; on doit donc calculer l'aire de la figure.

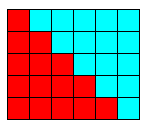Il suffit de lui faire faire un demi-tour et d'assembler : on obtient un rectangle de hauteur 5 et de base 6. Son aire vaut 30 et la somme cherchée vaut 30/2 = 15. C'est d'ailleurs ce qui conduit à la formule donnant la somme des termes d'une suite arithmétique.

Si on somme les naturels, on obtient successivement : 1, 3, 6, 10, 15, 21, 28,... et tout bon élève reconnaît les coefficients binomiaux donnant le nombre de combinaisons de n objets pris 2 à 2. Mais quel est le rapport avec la somme des n-1 premiers naturels ?

En y réfléchissant un peu, on voit que l'on peut calculer le nombre de paires d'un ensemble de n éléments (par exemple les entiers de 1 à \(n\) de la manière suivante : on compte d'abord le nombre de paires contenant \(n\) : il y en a évidemment \(n-1\). Cela fait, on compte celles contenant \(n-1\) et pas \(n\). Il y en a \(n-2\), ainsi de suite et l'on trouve que le nombre de paires extraites d'un ensemble de \(n\) éléments vaut \(n + n-1 + n-2 + .....+ 3 + 2 + 1\), c'est-à-dire précisément la somme des \(n-1\) premiers naturels.

Au passage, nous avons rencontré une série remarquable :

1   3   6  10  15  21  28  36  45 ....

Calculons les différences de termes consécutifs :

1   3   6  10  15  21  28  36  45 ....
   2   3   4   5   6   7   8   9  ....

et continuons de la même manière :

     1   3   6  10  15  21  28  36  45 ....
        2   3   4   5   6   7   8   9  ....
          1   1   1   1   1   1   1   1 ...
            0   0   0   0   0   0   0  ....
			

et le reste n'offre plus d'intérêt. En effectuant les différences successives on arrive à partir de la troisième étape à 0.

Arrêtons-nous un instant car il y a là peut-être quelque chose d'intéressant.

Tout d'abord ces suites forment un espace vectoriel : c'est évident, on peut les additionner, les soustraire, les multiplier par un nombre... et tout continue à fonctionner. Mais il y a peut être encore plus intéressant. Une suite \(a_1, a_2, a_3, ... a_n, ...\) est en fait une fonction définie sur les naturels. Pourquoi ne l'écrit-on d'ailleurs pas \(a(1), a(2), a(3), ..., a(n), ...\)? Bien souvent on peut la prolonger comme une fonction définie sur les entiers. L'exemple ci-dessus montre clairement que c'est très simple.

Retournons les choses ; on connaît les différences et on doit retrouver les nombres :

... 0   0   0   0   0   0   0   0   0   0   0  ....
....  1   1   1   1   1   1   1   1   1   1   1 ...
...-3  -2  -1   0   1   2   3   4   5   6   7  ....
....  3   1   0   0   1   3   6  10  15  21  28 ...
			

On aurait d'ailleurs pu remarquer que \(a_n\) vaut \(n(n-1)/2\) et calculer de cette manière les termes de la suite correspondant à des indices négatifs. Mais alors on est tenté de poursuivre et après être passé de n naturel à n entier, passer à \(n\) rationnel ou réel et, en fin de compte, étudier la fonction de la variable réelle \(x : a(x) = x(x-1)/2\).

Si on nous donne une fonction, en général on amorce son étude en calculant la dérivée première et éventuellement on poursuit en calculant les dérivées d'ordre supérieur. Mais qu'avions-nous fait ? Nous avions calculé les différences \(a_{i+1} - a_i\), ce qui peut s'écrire \(a(i + 1) - a(i)\) ou bien encore \(a(i + 1) - a(i)/(i + 1) - 1\). Est-ce très différent de \(a(x + h) - a(x)/(x + h) - x\), lorsque \(h=1\) ?

Les suites de différences correspondent en fait aux valeurs des dérivées d'ordre successif. En particulier si les différences d'ordre \(n\) sont nulles, cela correspond à une dérivée d'ordre n qui est nulle. Mais alors ? La dérivée d'ordre \(n-1\) est constante, celle d'ordre \(n-2\) est linéaire, et ainsi de suite.

Cette remarque peut alors nous aider à résoudre certains exercices. Soit, par exemple, à calculer la somme des carrés des \(n\) premiers naturels.

            1   4   9  16  25  36...
              1   5  14  30  55 ....
			

Comme tout à l'heure, retournons les choses :

              1   5  14  30  55 ....
            1   4   9  16  25  36...
              3   5   7   9  11 ....
                2   2   2   2   2...
                  0   0   0   0 ....
			

Les différences quatrièmes sont nulles, les différences troisièmes sont constantes,...et la fonction est donc du 3 ^e degré.

Essayons donc une fonction générale de type \(f(n) = an^3 + bn^2 + cn + d\) ; il ne reste qu'à calculer \(a, b, c \text{ et } d\). Pour cela si \(n=0, f(n)=0\) ; ensuite \(f(1)=1, f(2)=5 \text{ et } f(3)=14\). Cela conduit au système :

\[ \left\{\begin{array}{l l} d = 0\\ a + b + c + d = 1\\8a + 4b + 2c + d = 5\\27a + 9b + 3c + d = 14\\ \end{array} \right. \]

et en résolvant ce système, on obtient facilement :

\[f(n) = n(2n + 1)(n + 1)/6\]

Pour les sceptiques il reste toujours la bonne vieille méthode de démonstration par induction ; mais le problème c'est ... qu'il faut d'abord deviner le résultat !