Tôt ou tard, chacun d'entre nous est amené à emprunter de l'agent que ce soit pour effectuer l'achat d'une voiture, de mobilier ou alors d'un appartement, d'une maison.
On s'adresse alors à une institution de crédit pour obtenir un prêt remboursable, mensuellement s'il s'agit d'une "petite" somme ou annuellement si le montant est plus important. Il est évident que l'on souhait trouver la solution la moins onéreuse, mais les conditions de prêt ne sont pas toujours (et pour cause) énoncées clairement. Il faut en fait trouver l'organisme financier où le taux de chargement est le plus bas possible.
Supposons ce taux connu, et pour faciliter les calculs, prenons un exemple où le taux annuel est de \(10%\) ! Supposons que je souhaite emprunter \(100000\) €; que je rembourserai en \(6\) ans. Un de mes amis dispose de cette somme et est disposé à me la prêter, mais il ne veut pas me faire de cadeau.
S'il plaçait son argent en banque il recevrait (sans rien faire; que c'est immoral !) \(110000\) € après la première année, \(121000\) € après la deuxième année et ainsi de suite; à la fin de la sixième année il serait à la tête d'un capital de \(177156\) €.
Il est donc d'accord pour me prêter \(100000\) € que je lui rembourserai en \(6\) annuités de même montant, mais il ne veut rien perdre. Pour cela il placera le premier versement qui lui rapportera des intérêts pendant \(5\) ans, ensuite le deuxième versement qui produira des intérêts pendant \(4\) ans et ainsi de suite; il recevra enfin le sixième et dernier versement.
Bien entendu à la fin des \(6\) ans il souhaite disposer de \(177156\) € comme s'il avait placé son capital initial au taux annuel de \(10%\).
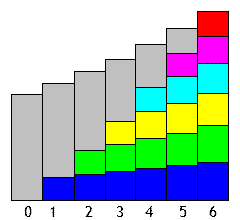
Les zones grisées représentent l'évolution du capital emprunté et les zones colorées celle des montants remboursés.
Si \(A\) désigne le montant du remboursement annuel, au bout des six années mon ami disposera, en posant r=10%, de: \(A.(1+r)^5 + A.(1+r)^4 + ... + A = 7,71561.A\). Cette somme doit être égale à \(177156,1\) € et il est donc facile de calculer \(A=177156,1\) €/\(7,71561~=~22960,7..\) €.
Pour envisager toutes les hypothèses, supposons qu'au cours de la troisième année je gagne à la loterie (plus exactement que je perde un peu moins que d'habitude !). Je souhaite alors m'acquitter de ma dette. Combien dois-je payer à la fin de cette troisième année ?
Au bout de \(3\) années de crédit mon ami aurait disposé sur son compte en banque de \(133100\) €. Il possède déjà \(22960,7\) € qui ont produit des intérêts pendant \(2\) ans et de \(22960,7\) € qui ont porté intérêt pendant un an. Cela représente \(22960,7\) €.\((1+r)^2 + 22960,7\) €.\((1+r)\) = \(27782,5\) € \(+ 25256,8\) € \(= 53039,3\)€. Il reste donc à lui payer la différence, soit \(133100\) € \(- 53039,3\) € \(= 80060,7\) €. Cela représente la valeur du rachat de ma dette.
Essayons à présent de généraliser cette situation en imaginant un prêt d'un capital C au taux de r (par période) remboursable en n périodes par versement d'un montant A.
Désignons par \(u=1+r\) le coefficient par lequel un capital est multiplié au bout d'une période.
La valeur \(V\) du capital \(C\) au bout des \(n\) périodes sera: \(V=C.u^n\)
Le premier versement rapporte des intérêts pendant \(n-1\) périodes, le deuxième pendant \(n-2\) périodes, et ainsi de suite. Au total la valeur \(V'\) des versements sera égale à:
\[ V' = A.u^{n-1} + A.u^{n-2} + ... + A.u + A \] ou encore: \[ V' =A.(u^n-1)/(u-1) \]Pour que le prêt soit équitable, il doit y avoir égalité: \(V = V'\), c'est-à-dire :
\[ C.u^n = A(u^n-1)/(u-1) \]Cette équation permet de déterminer \(A\) connaissant le capital emprunté \(C\), le nombre de remboursements \(n\) et le taux d'intérêt \(r\) \((u =1+r)\).
A titre d'exemple, voici un tableau donnant les annuités pour un capital de 100.000 € en fonction de la durée du prêt et du taux d'intérêt.
| 5% | 6% | 7% | 8% | 9% | 10% | |
|---|---|---|---|---|---|---|
| 10 ans | 12951 | 13587 | 14238 | 14903 | 15582 | 16275 |
| 15 ans | 9634 | 10296 | 10980 | 11683 | 12406 | 13147 |
| 20 ans | 8024 | 8719 | 9439 | 10185 | 10955 | 11746 |
et un tableau donnant les mensualités pour un prêt de 10.000 € à court terme:
| 4% | 6% | 8% | 10% | 12% | 14% | |
|---|---|---|---|---|---|---|
| 12 mois | 867 | 883 | 900 | 917 | 933 | 950 |
| 24 mois | 450 | 467 | 483 | 500 | 517 | 530 |
| 36 mois | 311 | 328 | 345 | 361 | 378 | 395 |
Dans la pratique, les prêteurs donnent souvent pour un capital \(C\) et un nombre \(n\) de remboursements le montant \(A\) à payer et dissimulent soigneusement (et pour cause !) la valeur de \(r\). Certains vont même jusqu'à faire le calcul suivant: "Vous remboursez au total \(n.A\) pour un emprunt de \(C\); les intérêts s'élèvent à \(n.A - C\) et le taux vaut donc \((n.A-C)/n\).
Dans l'exemple initial ils calculent de la manière suivante: 6 remboursements de 22.960,7 € = 137.764,4 €, donc 37.764,4 € d'intérêt en \(6\) ans ou 6.294,1 € par an. L'intérêt ne serait donc que de \(6.29\)% !!!
Enfin comment calculer le remboursement anticipé, la valeur de rachat de l'emprunt?
Si k remboursements ont été effectués, le montant B à verser doit être tel que:
\[ C.u^n = A.u^{n-1} + A.u^{n-2} + ... + A.u^{n-k} + B.u^{n-k-1} \] ou encore \[ C.u^n = A.(u^{n-1} + u^{n-2} + ... + u^{n-k}) + B.u^{n-k-1} \] d'où \[ B = C.u^{k+1} - A.u.(u^k-1)/(u-1) \]