La génétique progresse à pas de géant et on arrive à l'heure actuelle à déceler de nombreuses maladies associées à un gène "déformé". Si N désigne le gène normal, que nous supposerons dominant, et M le gène mutant ou "malade" et récessif, il y aura trois types d'individus dans la population: ceux de type (N,N) qui seront sains, ceux de type (N,M) qui seront porteurs et ceux de type (M,M) qui seront malades. Certaines de ces maladies sont fort graves et les enfants qui en sont atteints ont une espérance de vie fort réduite: quelques mois, voire quelques années. Ils décéderont avant d'être en âge de procréer. Cette situation aura donc une incidence dans l'évolution de la population.

Dans un autre article sur la couleur des yeux , nous avions étudié l'évolution d'une population où la modification d'un gène était sans conséquence sur la durée de vie. Nous avions vu qu'après une génération, la répartition des individus était stabilisée. C'était la fameuse loi de Hardy-Weinberg.

Ce résultat n'est évidemment pas valable dans le cas où l'on s'intéresse à un gène N dont l'allèle M entraîne une mortalité précoce. Remarquons immédiatement que ce gène doit être récessif sinon les individus de type (M,M) et (N,M) disparaîtraient tous deux sans progéniture et la population-mère restante serait uniquement composée d'individus de type (N,N). Nous supposerons, comme dans l'autre article, que la présence de l'un ou l'autre gène ne dépend pas du sexe et que les mariages se feront "au hasard".

Le gène M étant récessif, les individus de type (M,M) seront atteints et ne feront pas partie de la population-mère. Celle-ci ne comportera cette fois que deux types d'individus: les sains, que nous désignerons par S, de type (N,N), et les porteurs, désignés par P, de type (N,M).

Les individus S transmettront toujours un gène N. Par contre les individus P transmettront une fois sur deux un gène N et une fois sur deux un gène M. Ceci nous conduit à désigner par a , le nombre de S et par 2 b , le nombre de P.

Faisons un petit diagramme pour voir ce qui se passera dans la population-fille.

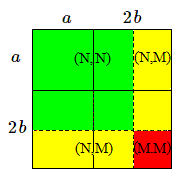
En rouge, nous aurons les individus de type (M,M) qui ne survivront pas assez longtemps pour se reproduire.

La population totale vaut \((a+2b)^2-b^2=(a+b)(a+3b)\); le nombre d'individus sains vaut: \((a+b)^2\) et celui de porteurs: \(2(a+b)b\).

Le rapport porteurs : sains qui était \(a:2b\) dans la population-mère devient \(a':2b'\) avec \(a'=(a+b)/(a+3b)\) et \(2b'=2b/(a+3b)\) Il passe donc de la valeur \(a:2b\) à la valeur \(a':2b'=(a+b):2b\) À la génération suivante, il sera égal à \((a+2b):2b\), ensuite, il vaudra \((a+3b):2b\) et ainsi de suite.

Si on préfère travailler en pourcentages, celui d'individus sains vaut au départ : \(a/(a+2b)\); une génération plus tard, il passe à la valeur \((a+b)/(a+3b)\), puis à la deuxième génération, il vaudra \((a+2b)/(a+4b)\) et à la n ^e génération, \((a+nb)/(a+(n+2)b)\). Ce rapport a pour limite 1 (100%) lorsque n tend vers l'infini. On voit donc que dans la situation envisagée, la loi de Hardy-Weinberg n'est plus valable.

Cette loi constatait que les rapports entre les différents types d'individus restaient constants tout au long des générations. Pour l'instant, ces rapports évoluent, et ceci, dans un sens favorable. La population d'individus porteurs diminue et, par conséquent, la proportion de malades diminue également. Ce résultat pose un problème éthique.

Si on arrive à augmenter la durée de vie des malades jusqu'à dépasser l'âge de procréation, la situation globale ne s'améliorera plus. Au contraire, ne rien faire, diminuera la proportion des malades.

La mathématique n'apporte pas de réponse à ce pénible dilemme.