 Les photographes professionnels utilisent encore un appareil, appelé chambre technique, qui ressemble fort à ceux utilisés au début de la photographie.
Cette chambre technique est composée de deux parties: l'avant sur lequel est monté un objectif et le dos sur lequel viendra prendre place le film ou le capteur; ces deux parties, reliées par un soufflet, sont montées sur un rail et peuvent être déplacées en tous sens afin d'obtenir les effets désirés.
L'observation de l'image sur le dépoli se fait encore aujourd'hui avec la tête sous un drap noir !
Les photographes professionnels utilisent encore un appareil, appelé chambre technique, qui ressemble fort à ceux utilisés au début de la photographie.
Cette chambre technique est composée de deux parties: l'avant sur lequel est monté un objectif et le dos sur lequel viendra prendre place le film ou le capteur; ces deux parties, reliées par un soufflet, sont montées sur un rail et peuvent être déplacées en tous sens afin d'obtenir les effets désirés.
L'observation de l'image sur le dépoli se fait encore aujourd'hui avec la tête sous un drap noir !
Vous avez certainement déjà observé sur certaines affiches publicitaires l'utilisation de la profondeur de champ pour mettre en valeur le produit dont on vante les mérites. En observant plus attentivement, on constate que le plan de netteté n'est pas nécessairement perpendiculaire à la direction de visée, comme cela se passe sur les appareils usuels des amateurs.
Si le produit est un produit alimentaire, le plan de netteté sera généralement parallèle à la table sur laquelle est présenté le produit. Cela est précisément possible grâce à l'utilisation d'une chambre technique et à la règle de Scheimpflug (géodésiste autrichien) qui est une belle application du théorème de Desargues.
Rappelons tout d'abord quelques règles élémentaires de l'optique géométrique.
L'objectif de l'appareil peut être assimilé à une lentille convergente; un rayon parallèle à l'axe optique sera réfracté par le foyer; un rayon passant par le centre optique ne sera pas dévié et enfin un rayon passant par le foyer objet ressortira parallèlement à l'axe. Deux de ces propriétés nous suffisent d'ailleurs pour connaître l'image d'un point quelconque. La construction de l'image est rappelée sur la figure qui suit.
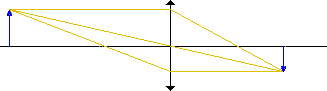
Il est bien évident que l'image d'un plan perpendiculaire à l'axe optique sera, avec un bon objectif bien corrigé!, un plan perpendiculaire à l'axe optique, et cette image sera recueillie sur le film disposé à l'endroit de ce plan. Par conséquent si l'on veut qu'un plan non perpendiculaire à l'axe soit net sur la photo, il faudra donc faire basculer le dos (où se trouve placé le film) de la chambre technique.
C'est ici que Scheimpflug intervient. Il affirme que le plan objet, le plan de l'objectif et le plan de l'image sont trois plans passant par une même droite. Et c'est Desargues qui va nous aider à prouver cette propriété.
Rappelons tout d'abord la célèbre configuration de points et de droites connue sous le nom de théorème de Desargues .
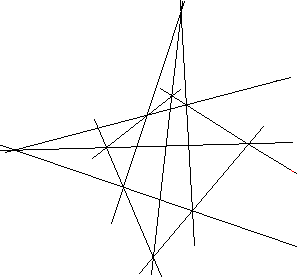
Le théorème de Desargues dit essentiellement que la configuration dessinée ci-dessus est réalisable, c'est-à-dire que si l'on commence à dessiner la figure les trois derniers points construits (les trois dernières droites construites) sont colinéaires (sont concourantes).
Dans notre cas, considérons la figure représentant la situation décrite plus haut. Soient \(p\), \(q\) et \(i\), 3 points situés dans le plan objet \(P\) représenté ici perpendiculairement au dessin. Le point \(i\) est sa propre image car situé dans le plan de l'objectif perpendiculaire à l'axe optique; les images \(p', q'\) images de \(p\) et \(q\) sont construites en utilisant les lois de l'optique géométrique.
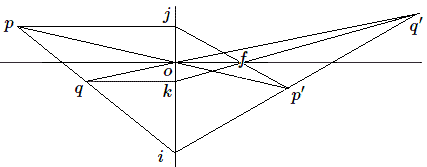
Les rayons parallèles à l'axe par \(p\) et \(q\) coupent le plan de l'objectif en \(j\) et \(k\). Considérons à présent les deux triangles \(opq\) et \(fjk\). Les droites joignant les sommets homologues sont concourantes et se coupent à l'infini: il s'agit de trois rayons parallèles à l'axe optique. Le théorème de Desargues nous permet donc de conclure que les points d'intersection des côtés homologues c'est-à-dire \(i, p', q'\) sont alignés.
Si nous fixons \(i\) et \(p\) et que nous faisons varier \(q\) sur la droite \(ip\), l'image \(q'\) variera sur la droite \(ip'\). La droite \(ip\) a pour image la droite \(ip'\) et le plan perpendiculaire \(P\) aura donc pour image le plan perpendiculaire à l'axe optique \(P'\) passant par \(ip'\).
Pour le photographe qui désire réaliser une photo où le plan de netteté est situé en \(P\), il en résulte la règle énoncée plus haut. Il détermine tout d'abord la droite \(D\) d'intersection de \(P\) avec le plan de son objectif (la perpendiculaire à \(i\)) et ensuite il bascule le dos de la chambre de telle manière que le plan de celui-ci passe par \(D\). Le résultat sera celui désiré.
Il faut toutefois remarquer que le fait que le dos n'est pas perpendiculaire à l'axe optique peut entraîner une perspective assez inhabituelle.