Introduction
Cela peut paraître quelque peu surprenant, mais Mercure est bel et bien la planète la proche de la Terre en moyenne. Si l’on considère la distance minimale, Vénus est bien notre plus proche voisine.
Fait étonnant, Mercure est la planète la plus proche de toutes les autres planètes du système solaire en moyenne.
Cela peut paraître surprenant à première vue tant on est familier avec cette représentation héliocentrique:
Approche mathématique
Pour effectuer notre calcul de distance moyennes, il y a d’abord quelques considérations à prendre en compte:
Inclinaison orbitale
Toutes les planètes du système solaire n’orbitent pas dans un même plan. En effet, peu importe le plan de référence choisi:
- Écliptique: plan défini par la rotation de la Terre autour du Soleil ;
- Équateur du Soleil: plan défini par l’axe de rotation du Soleil ;
- Plan invariable: Défini par le barycentre du système solaire et qui est perpendiculaire au vecteur du moment angulaire du système ;
Il existe un angle d’environs 7° entre les deux planètes ayant les inclinaisons plus sévères (Terre et Mercure), certains corps transneptuniens possèdent des angles bien plus importants (Pluton 17°). Peut-être que cette considération n’est pas capitale comme l’inclinaison orbitale moyenne est de 2.6° \(\pm\) 2.2°, et que l’on pourrait considérer les planètes comme étant coplanaires.
Excentricité
L’excentricité d’une planète est une mesure de la déviation de son orbite par rapport à un cercle parfait. Elle est définie par un nombre sans dimension compris entre 0 et 1, avec 0 comme un cercle parfait. À l’exception de Mercure (0.2), fortement influencé par sa proximité immédiate avec le Soleil, les autres planètes ont une excentricité moyenne de 0.04 \(\pm\) 0.04, soit très proche de cercles. Faire l’hypothèse que les orbites sont circulaires et concentriques n’est pas totalement hors sujet.
Perturbations gravitationnelles
Jupiter est connue, de par sa masse importante, pour avoir des impacts sur la rotation des autres corps du système solaire. Il peut être légitime de considérer le cas simple où seuls les corps sont deux-à-deux considérés et ce, en absence de toutes autres interactions avec les autres planètes.
Précession du périastre
La précession du périastre (ou précession du périhélie, dans le cas des orbites autour du Soleil) est le phénomène par lequel l’axe majeur de l’orbite elliptique d’une planète ou d’un autre corps céleste tourne lentement autour du corps central (comme le Soleil). En d’autres termes, le point de l’orbite le plus proche du Soleil (le périastre ou périhélie) change de position au fil du temps. Ce phénomène est lié entièrement expliqué par la relativité générale et, en partie, par des explications newtoniennes mais n’a, au final, qu’une très faible influence sur l’orbite.
Mathématiques
Pour des raisons de symétrie, calculer la distance moyenne à partir d’une position quelconque de \(P2\) est équivalente à choisir une position pour \(P2\) fixe et calculer la distance à chaque position de \(P1\).
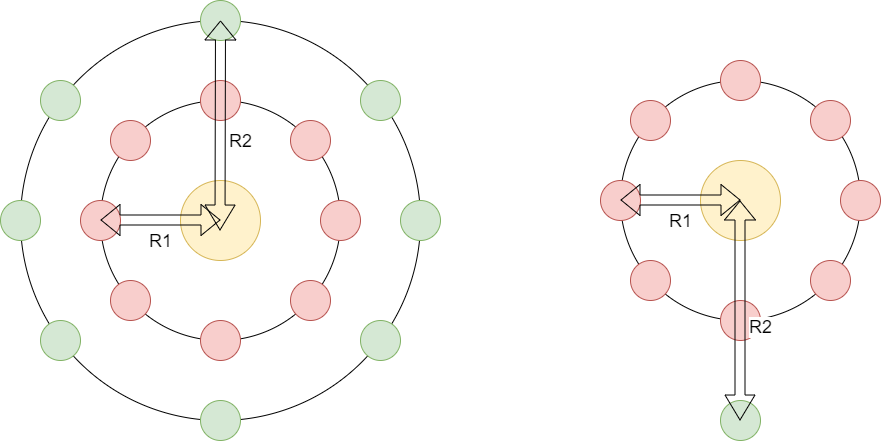
Si l'on place un référentiel à la position de \(P2\), notre planète \(P1\) aura pour équation:
$$ \begin{cases} x_1(t) = R1 * cos(t) + R2 \\ y_1(t) = R1 * sin(t) \end{cases} $$et \(P2\):
$$ \begin{cases} x_2(t) = 0 \\ y_2(t) = 0 \end{cases} $$On applique Pythagore et on obtient l'expression suivante:
$$ \sqrt{(R1 ~ cos(t) + R2 - 0)^2 + (R1 ~ sin(t) - 0)^2} = \sqrt{R1^2 + 2R1R2 ~ cos(t) + R2^2} $$Ensuite, on profite de l'identité trigonométrique \(cos(2x) = 1 - 2 sin^2(x)\) et en réarrangeant les termes, on obtient:
$$\sqrt{R1^2 + 2R1R2 ~ \cos(t) + R2^2}$$ $$\sqrt{R1^2 + 2R1R2 ~ (1 - 2 \sin^2(t/2)) + R2^2}$$ $$\sqrt{R1^2 + 2R1R2 - 4R1R2 \sin^2(t/2)) + R2^2}$$ $$\sqrt{(R1 + R2)^2 - 4R1R2 \sin^2(t/2))}$$ $$\sqrt{1 - \frac{4R1R2}{(R1 + R2)^2} \sin^2(t/2))}$$ $$ \int_{0}^{\pi/2} \sqrt{1 - k^2 \sin^2{\phi}} d\phi \text{ où } k = \frac{2\sqrt{R1 R2}}{R1 + R2} $$Cette dernière équation est appelée intégrale elliptique de la 2e espèce, définie sur un quadrant du cercle, et est traditionnellement noté par \(E(.)\). Ensuite, il ne reste qu'à prendre l'intégrale des 4 quadrants, multiplié par la distance entre les deux corps et divisé par le périmètre du cercle complet. On obtient:
$$ \text{distance moyenne} = 4 E(\frac{2\sqrt{R1 R2}}{R1 + R2}) \frac{(R1 + R2)}{(2 \pi)} $$Pour les différentes planètes du système solaire, on obtient le résultat suivant:
| mercury | venus | earth | mars | jupiter | saturn | uranus | |
|---|---|---|---|---|---|---|---|
| venus | 0.75 | ||||||
| earth | 0.98 | 1.12 | |||||
| mars | 1.43 | 1.54 | 1.66 | ||||
| jupiter | 4.79 | 4.78 | 4.82 | 4.94 | |||
| saturn | 8.88 | 8.78 | 8.76 | 8.79 | 9.9 | ||
| uranus | 18.13 | 17.9 | 17.78 | 17.66 | 18.1 | 19.54 | |
| neptune | 28.67 | 28.31 | 28.11 | 27.87 | 27.6 | 28.73 | 32.43 |
Approche numérique
Une question émerge suite à notre approche mathématique, à quel point est-elle correcte ? Nos approximations sont-elles légitimes ou mènent-elles à des résultats éloignés de la réalité ?
Pour cela, nous pouvons adopter une approche numérique. On peut simuler le trajet réel des planètes dans le système solaire sur de très longues périodes et calculer la distance moyenne.
Si cela semble simple a priori, il y a néanmoins quelques complications:
- Les équations "exactes" sont particulièrement velues comme elles font intervenir beaucoup de notions et sont vraiment lentes à évaluer.
- Les périodes de simulation se doivent d’être extrêmement longues comme il faut que les deux planètes se retrouvent aux "mêmes" positions. Sachant que Uranus a une période de révolution de 30’698 jours (terrestres) et Neptune de 60’216.8 jours, cela représente plus de 5 millions d’années !
- La stabilité numérique, il y a de nombreuses étapes dans le calcul qui peuvent entraîner de nombreuses erreurs d’arrondis, d’approximations, … Il peut être intéressant d’employer des algorithmes plus appropriés afin de limiter les erreurs comme l’algorithme de sommation de Kahan1.
Ici, grâce à la libraire "Astropy"2 en Python, j’ai simulé la distance moyenne sur 100’000 jours équidistribués dans la période totale de révolution des deux planètes. En considérant, d’abord toutes les planètes comme étant coplanaires, et puis une seconde fois en prenant en compte leur inclinaison orbitale. On obtient le tableau suivant:
| mercury | venus | earth | mars | jupiter | saturn | uranus | ||
|---|---|---|---|---|---|---|---|---|
| Math | venus | 0.75 | ||||||
| Simu 2D | 0.74 | |||||||
| Simu 3D | 0.78 | |||||||
| Math | earth | 0.98 | 1.12 | |||||
| Simu 2D | 0.99 | 1.09 | ||||||
| Simu 3D | 1.04 | 1.14 | ||||||
| Math | mars | 1.43 | 1.54 | 1.66 | ||||
| Simu 2D | 1.49 | 1.55 | 1.63 | |||||
| Simu 3D | 1.56 | 1.62 | 1.7 | |||||
| Math | jupiter | 4.79 | 4.78 | 4.82 | 4.94 | |||
| Simu 2D | 5 | 5.02 | 5.04 | 5.10 | ||||
| Simu 3D | 5.21 | 5.23 | 5.25 | 5.31 | ||||
| Math | saturn | 8.88 | 8.78 | 8.76 | 8.79 | 9.9 | ||
| Simu 2D | 9.19 | 9.2 | 9.21 | 9.25 | 9.88 | |||
| Simu 3D | 9.55 | 9.56 | 9.58 | 9.62 | 10.27 | |||
| Math | uranus | 18.13 | 17.9 | 17.78 | 17.66 | 18.1 | 19.54 | |
| Simu 2D | 18.417 | 18.421 | 18.43 | 18.45 | 18.77 | 19.58 | ||
| Simu 3D | 19.21 | 19.22 | 19.23 | 19.25 | 19.58 | 20.41 | ||
| Math | neptune | 28.67 | 28.31 | 28.11 | 27.87 | 27.6 | 28.73 | 32.43 |
| Simu 2D | 28.958 | 28.961 | 28.965 | 28.975 | 29.17 | 29.69 | 31.98 | |
| Simu 3D | 30.071 | 30.076 | 30.079 | 30.09 | 30.29 | 30.83 | 33.24 |
L’hypothèse de coplanarité des planètes est quand même forte. On remarque de grandes disparités entre le cas 2D et 3D. Si l’erreur demeure inférieure à 6% dans le cas 2D, elle grimpe quasiment à 10% dans le cas 3D.
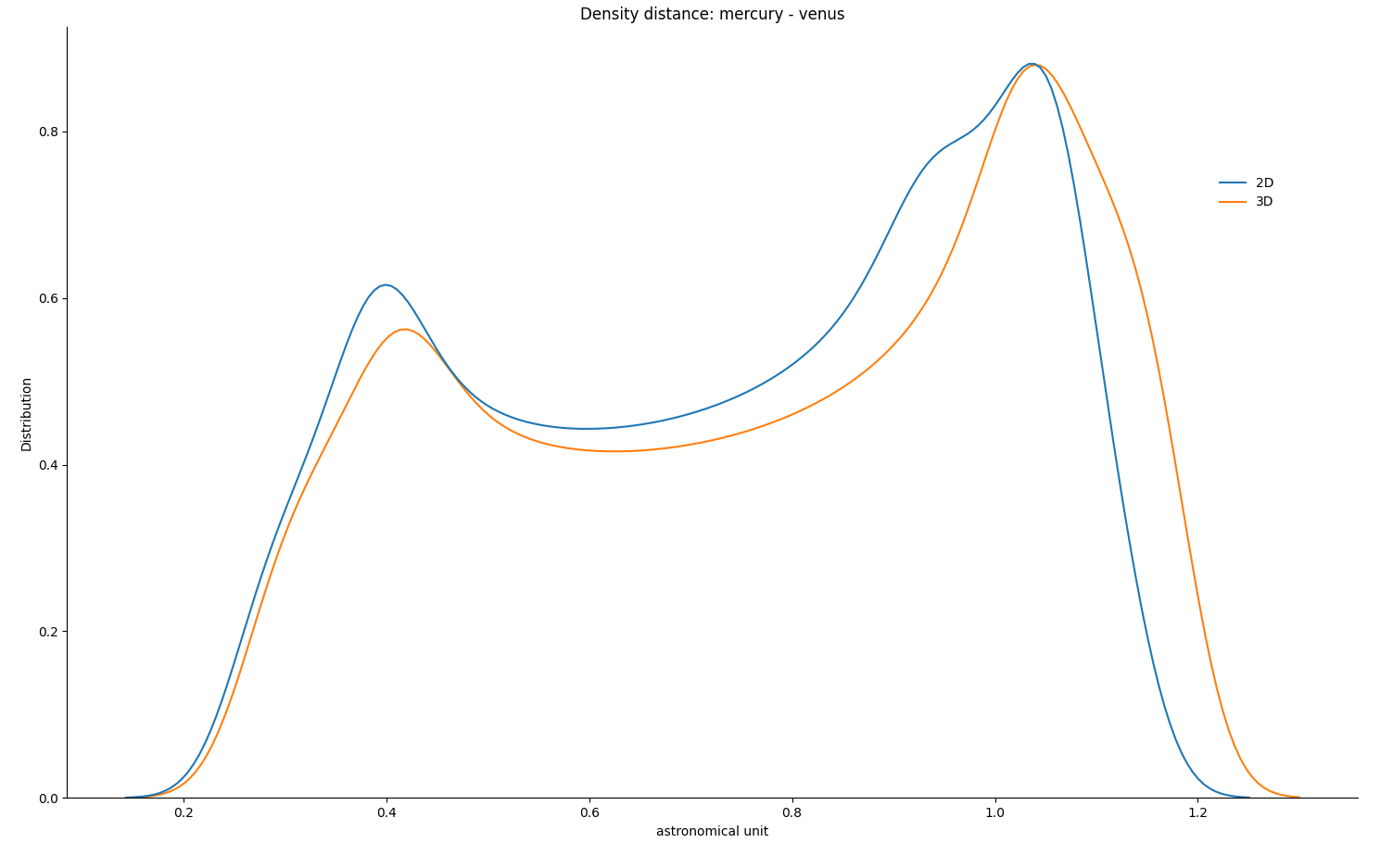
- Kahan, William. "Pracniques: further remarks on reducing truncation errors." Communications of the ACM 8, no. 1 (1965): 40.↩
- https://www.astropy.org/↩
En essayant de rationnaliser l’explication, Mercure demeure "proche" du Soleil et la distance reste assez similaire au cours de son orbite. Au contraire, quand Uranus et Neptune sont à l’exacte opposé du système Solaire, elles le sont pour un long temps, ce qui augmente énormément la moyenne.
Si on s'intéresse à la différence de distance de Mercure et Vénus par rapport à la Terre, on obtient le graphique suivant:
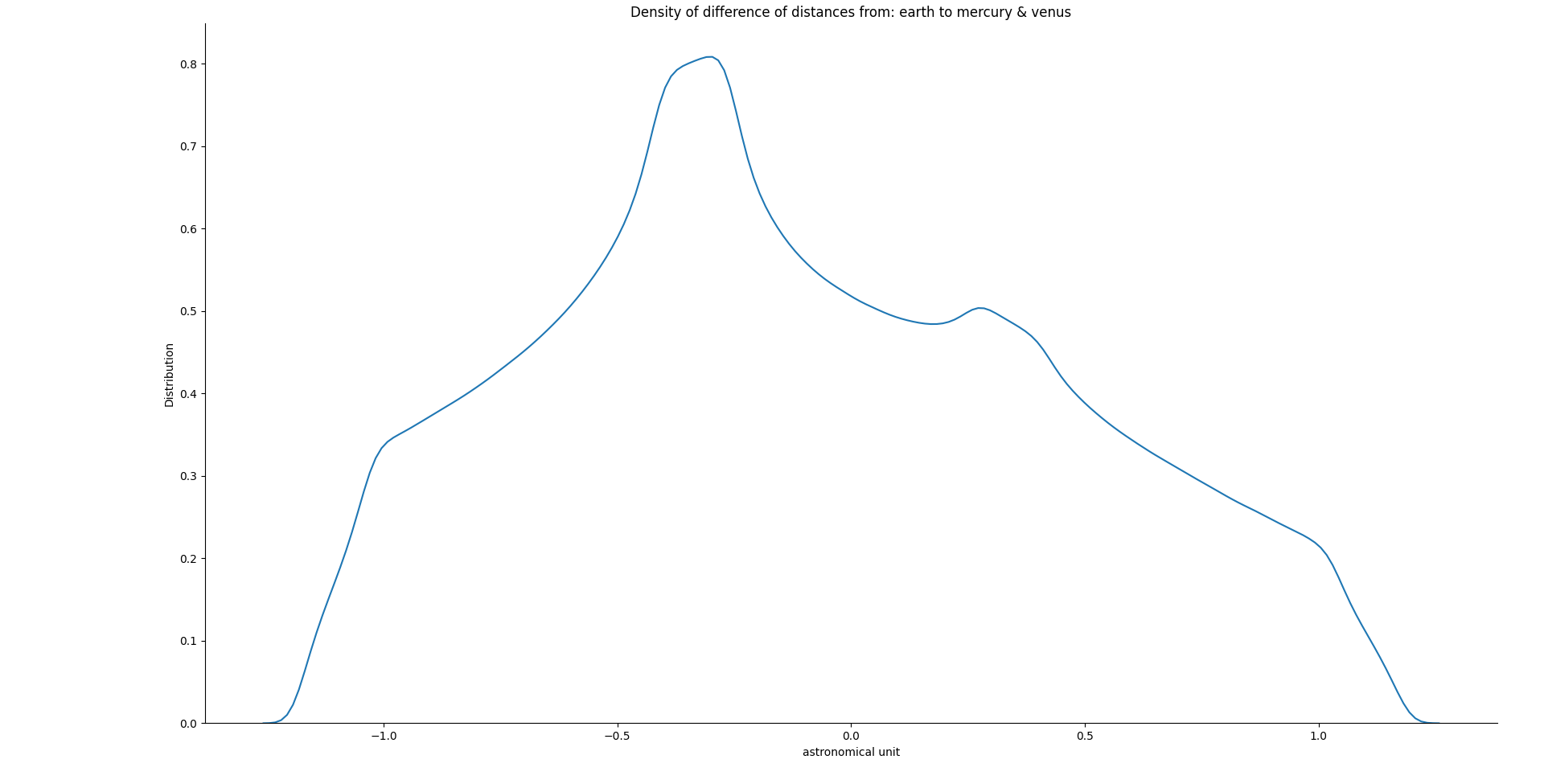
En majorité du temps (59%), la distance entre la Terre et Mercure est plus petite que celle entre Vénus et la Terre. La partie négative (à gauche) correspond à une distance inférieure de Mercure par rapport à Vénus (Mercure est donc plus proche) et, à droite, il s'agit de l'inverse, Vénus plus proche.
En écrivant cet article, je suis tombé sur cette référence écrite en 2019. Malgré des calculs que j'espère similaires, je note de larges différences au niveau des résultats présentés. J'ai beaucoup de mal à saisir leur origine.