Natacha apprend à lancer le poids. Ce sport n'est peut-être pas très féminin, mais elle s'entête. Cette fois je l'ai lancé trop verticalement, et évidemment il est retombé tout près de moi. (Heureusement que je ne l'ai pas lancé à la verticale, ce serait vraiment dangereux !) Maintenant c'est beaucoup mieux: je l'ai lancé beaucoup plus horizontalement et le poids est retombé plus loin. Toutefois je ne dois pas le lancer trop horizontalement; il faut lui donner la chance de monter pour redescendre plus loin. Comment faire ? Si je faisais la moyenne entre la verticale (angle de 90°) et l'horizontale (angle de 0°) ? Cette fois je vais le lancer à 45°. Ça y est ! J'ai battu mon record.

D'accord c'est la bonne solution, mais la démonstration n'est pas très scientifique. Comment poser le problème ?

Supposons que le lanceur soit infatigable et qu'à chaque tentative il lance le poids avec la même vitesse initiale \(V\) et que cette vitesse forme un angle \(\varphi\) avec l'horizontale. Plaçons la coordonnée \(x\) horizontale et la coordonnée \(y\) verticale et supposons le poids lancé à partir du point de coordonnées \((0, h)\). Calculons le mouvement. Regardons les composantes de l'accélération:

\[ \begin{array} {ll} a_x= 0 \\ a_y=-g \end{array} \]

À partir de l'accélération nous pouvons calculer les composantes de la vitesse. Puisque l'accélération est la dérivée de la vitesse par rapport au temps, il suffit d'intégrer les valeurs de l'accélération. De plus si \(t = 0\), alors la composante \(v_x\) vaut \(V\mathbf{cos~}\varphi \) et la composante \(v_y=V\mathbf{sin~}\varphi \). On obtient:

\[ \begin{array} {ll} v_x = V\mathbf{cos~}\varphi \\ v_y = -gt + V\mathbf{sin~}\varphi \end{array}\]

Voilà en ce qui concerne la vitesse. Si on désire obtenir les coordonnées, il suffit d'intégrer la vitesse, puisque la vitesse est la dérivée de l'espace par rapport au temps.

\[ \begin{array} {ll} x = Vt\mathbf{cos~} \varphi \\ y = -gt^2/2 + Vt\mathbf{sin~}\varphi + h \end{array} \]

Pour simplifier les choses supposons qu'à l'instant initial \(t = 0, h\) soit nul: cela signifie que le poids part du sol, ce qui est inexact mais proche de la réalité (songeons que cela peut également s'appliquer au lancement du marteau, du javelot...). Les équations se simplifient et on obtient:

\[ \begin{array} {ll} x = Vt\mathbf{cos~}\varphi \\ y = -gt^2/2 + Vt\mathbf{sin~}\varphi \end{array} \]

La trajectoire décrite par le poids est une parabole dont on obtient l'équation en éliminant le paramètre t entre les deux équations.

\[ y= -gx^2/2V^2\mathbf{cos~}^2\varphi + x\mathbf{sin~}\varphi/\mathbf{cos~} \varphi \]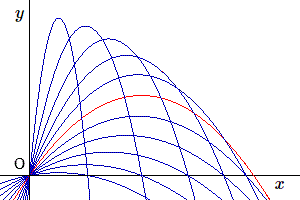

Voici comment se présentent les trajectoires lorsque l'angle \(\varphi \) varie. On voit qu'effectivement il semble que la meilleure manière de lancer le poids est de faire un compromis entre le lancement à la verticale et le lancement à l'horizontale. Mais nous pouvons préciser cette constatation.

Le poids retombe lorsque \(y=0\) ; on a donc l'équation:

\[ -gx^2/2V^2\mathbf{cos~}^2\varphi + x\mathbf{sin~}\varphi /\mathbf{cos~}\varphi =0 \]

Cette équation du second degré possède deux solutions: d'une part \(x=0\)(évidemment) et la solution qui nous intéresse :

\[ x=2V^2\mathbf{sin~}\varphi .\mathbf{cos~} \varphi /g=0 \]

Dès lors il est facile d'optimiser l'angle du lancer: \(2\mathbf{sin~}\varphi .\mathbf{cos~} \varphi \) doit être maximum ou encore \(\mathbf{sin~}2\varphi \) doit être maximum. On doit donc avoir \(2\varphi = 90°\) ou \(\varphi = 45°\) (la solution comprise entre 0° et 90°).

On remarque sur le graphique que toutes les paraboles correspondant aux différents angles de lancer "enveloppent" une courbe.

Pour préciser cette constatation, nous allons rechercher l'enveloppe d'une famille de courbes \(y=F(x,\lambda)\) où \(\lambda\) est un paramètre variable. Si l'équation de l'une d'elle est \(y=F(x,\lambda_0)\), on obtient le (ou les) point(s) de l'enveloppe situé sur cette courbe en recherchant son intersection avec une courbe voisine correspondant à une valeur \(\lambda_0+d\lambda \). Il faut donc résoudre le système des équations:

\[ \begin{array} {ll} y= F(x,\lambda_0) \\ y= F(x,\lambda_0+d\lambda)\end{array} \] En soustrayant membre à membre et en divisant par \(d\lambda \), on obtient un nouveau système: \[ \begin{array} {ll} y= F(x,\lambda_0) \\ 0= \frac {dF}{d\lambda}(x,\lambda_0) \end{array} \]

Pour chacune des valeurs de \(\lambda \) on obtient le (ou les) points de l'enveloppe. Pour obtenir l'équation de l'enveloppe il suffit donc d'éliminer le paramètre \(\lambda \).

Dans notre exemple, le paramètre est \(\varphi \). Nous obtenons le système d'équations:

\[ \begin{array} {ll} y = -gx^2/2V^2\mathbf{cos~}^2 \varphi + x\mathbf{sin~}\varphi/ \mathbf{cos~} \varphi \\ 0 = -gx^2\mathbf{sin~}\varphi/V^2\mathbf{cos~}^3\varphi + x/\mathbf{cos~}^2\varphi \end{array} \]

Une astuce de calcul simplifie les choses: il suffit d'utiliser comme variable \(\mathbf{tan~}\varphi \) et d'utiliser la formule \(1/\mathbf{cos~}^2\varphi =1+\mathbf{tan~}^2\varphi \). Le système d'équations devient:

\[ \begin{array} {ll} y=-gx^2(1 + \mathbf{tan~}^2\varphi)/2V^2 + x\mathbf{tan~}\varphi \\0=-gx \mathbf{tan~}\varphi/V^2+1 \end{array} \]

et en éliminant \(\mathbf{tan~}\varphi \) on obtient:

\[ y = -g/2V^2 x^2 + V^2/2g \]

ce qui est l'équation d'une parabole.

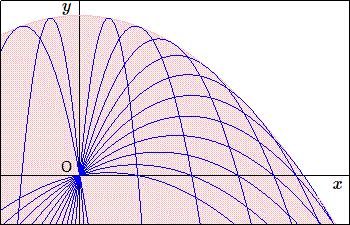
Cette courbe est connue depuis fort longtemps et est appelée parabole de sécurité . Le problème avait été étudié par les artilleurs, non point dans le cadre du lancement du poids, mais lors du tir de projectiles à partir d'un canon. Cette courbe délimite une zone en dehors de laquelle on est à l'abri du tir quelle qu'en soit la direction.