Dans l'enseignement traditionnel, les programmes des cours de physique et ceux de mathématiques ne sont généralement pas coordonnés. L'optique, et en particulier la réfraction, est étudiée alors que les fonctions goniométriques sinus et cosinus ne sont pas encore connues. De même, l'année suivante, on étudie en physique la mécanique, les mouvements rectilignes uniformes ou uniformément accélérés alors que les notions mathématiques utiles, la dérivée et l'intégrale, ne seront enseignées qu'un ou deux ans plus tard.

Revenons-en à l'optique. Que peut faire le physicien qui doit enseigner la réflexion et la réfraction pour expliquer le fonctionnement de quelques appareils utilisant des lentilles ou des miroirs ? Certes, la réflexion est un phénomène simple à expliquer. La lumière "rebondit" sur un miroir ; d'où l'analogie avec un plan de symétrie entre la lumière incidente et la lumière réfléchie. Le mathématicien peut même trouver prétexte à un exercice : étant donné un miroir, un point et son image sont reliés au miroir par deux rayons lumineux dont la longueur totale est minimale.

Hélas, quand il s'agit de la réfraction, phénomène bien plus courant cependant, le physicien est embarrassé car l'élève ne connait pas encore les fonctions goniométriques élémentaires. De son côté, le mathématicien serait bien en peine d'expliquer le phénomène aussi simplement que pour la réflexion. Pourrait-il dire qu'un point et son image sont reliés à la surface d'un dioptre par deux rayons lumineux dont la longueur totale est minimale ? Mais qu'entend-on par "longueur" minimale ? S'agit-il de la distance du trajet en nombre de mètres, ou bien de la durée du trajet exprimée en nombre de secondes ?

En fait, c'est la durée du trajet qui est minimale, phénomène compris par Pierre de Fermat . Que ce soit par réflexion ou par réfraction, le rayon lumineux suit toujours un trajet dont la durée est minimale !

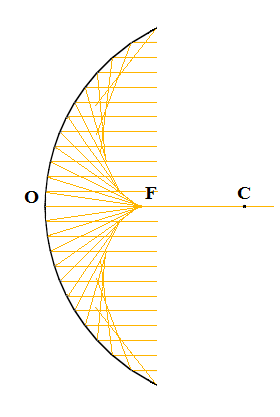
L'embarras du mathématicien grandit, car s'il peut très rapidement expliquer ce qu'est le sinus d'un angle, il lui sera bien plus difficile de se lancer dans un problème d'extremum. Pourtant, deux ans plus tard, après avoir manipulé les dérivées , les problèmes d'extréma sont devenus simples. Ne serait-il pas utile de reprendre comme application intéressante et utile, le phénomène de réfraction ? Cela permettrait d'expliquer la règle simpliste du rapport des sinus par le principe de Fermat . De plus, comme la réfraction est à la base de la plupart des instruments d'optique, miroirs et lentilles, le mathématicien pourrait même faire remarquer que la "convergence" des rayons vers un foyer est fausse et qu'il ne s'agit que d'une approximation valable pour des rayons ne s'écartant pas trop de l'axe optique de l'instrument.

Essayons d'appliquer le principe de Fermat dans le cas d'une réfraction d'un rayon lumineux traversant le dioptre séparant deux milieux distincts par exemple l'air et l'eau, comme on peut l'observer simplement, ou l'air et le verre dont la réfraction est à la base de la construction des lentilles utilisées dans les appareils optiques.

Le phénomène de réfraction est basé sur le fait que la vitesse de la lumière dépend de la nature du milieu traversé. On observe qu'il est plus facile de se déplacer dans l'air que dans l'eau ; le 100m se court maintenant en moins de 10 secondes alors qu'il se nage en moins de 50 secondes ! C'est l'origine d'un problème connu sous le nom "Le maître-nageur et la baigneuse" : un maître-nageur sur la plage aperçoit une baigneuse en difficulté dans l'eau. Il doit donc la secourir le plus rapidement possible en effectuant une course sur le sable, suivie d'une nage dans l'eau, deux éléments où sa vitesse de déplacement sera fort différente.

Représentons cela par le schéma ci-après :

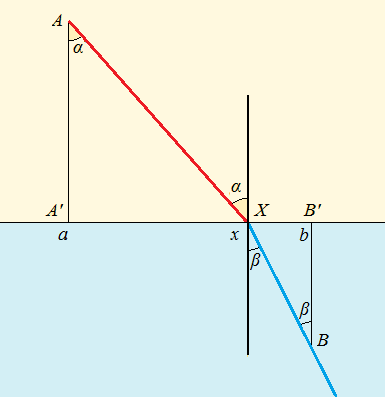
Dans l'exemple physique, le rayon lumineux part de \( A \) traverse le dioptre en \( X \) et aboutit en \( B \). La séparation air et eau sera prise comme axe des abscisses. Soient \( A' \) et \( B' \) les projections orthogonales de \( A \) et de \( B \) sur l'axe des abscisses. En résumé, le rayon lumineux part du point \( A (a, h_a) \), traverse le dioptre en \( X(x, 0) \) et aboutit en \( B(b, h_b) \). En \( X \), la normale au dioptre forme un angle \( \alpha \) avec le rayon incident et un angle \( \beta \) avec le rayon réfracté.

Avec ce choix de coordonnées, le segment \( A'X \) a pour longueur \( x-a \), et le segment \( XB' \) mesure \( b-x \). Calculons la longueur des trajets \( AX \) et \( XB \) : \[AX=\sqrt{~{h_a}^2+(x-a)^2}~~\text{et}~~XB=\sqrt{~{h_b}^2+(b-x)^2}\] Si \( v_a \) et \( v_b \) désignent les vitesses respectives de la lumière dans l'air et dans l'eau, la durée des deux trajets sera : \[t_a = \frac{\sqrt{~{h_a}^2+(x-a)^2}}{v_a} ~~\text{et}~~ t_b = \frac{\sqrt{~{h_b}^2+(b-x)^2}}{v_b}\] Le temps total \( t = t_a \) et \( t_b \) sera une fonction de \( t(x) \) qui devra être minimisée: \[t(x)=\frac{\sqrt{~{h_a}^2+(x-a)^2}}{v_a}+\frac{\sqrt{~{h_b}^2+(b-x)^2}}{v_b}\]

Pour obtenir la valeur de \( x \) correspondant à ce minimum, calculons la dérivée de \( t(x) \).

\[t'(x)=\frac{x-a}{v_a~\sqrt{~{h_a}^2+(x-a)^2}}-\frac{b-x}{v_b~\sqrt{~{h_b}^2+(b-x)^2}}\]

Quelle est la valeur de x qui annule cette dérivée ? Voilà qui semble bien compliqué ! Heureusement les numérateurs et dénominateurs ont un sens géométrique simple et on obtient:

\[t'(x)=\frac{A'X}{v_a.AX}-\frac{B'X}{v_b.BX}\]

Chacun des deux termes de cette différence concerne un triangle rectangle : \( AA'X \) pour le premier et \( BB'X \) pour le second. On y reconnaît le rapport d'un côté à l'hypoténuse et donc la définition d'un sinus. \[\frac{A'X}{AX}=\mathbf{sin~}\alpha~~\text{et}~~\frac{B'X}{BX}=\mathbf{sin~}\beta \] On obtient finalement \[t'(x) = 0 \iff \frac{\mathbf{sin~}\alpha}{v_a}-\frac{\mathbf{sin~}\beta}{v_b}=0\iff \frac{\mathbf{sin~}\alpha}{v_a}=\frac{\mathbf{sin~}\beta}{v_b}\]

La loi de réfraction s'exprime traditionnellement en utilisant les indices de réfraction. L'indice de réfraction \( n \) d'un milieu est défini comme le rapport entre la vitesse \( c \) de la lumière dans le vide et sa vitesse \( v \) dans le milieu considéré. On a donc \( n = \frac{c}{v} \). Il est donc inversement proportionnel à la vitesse de la lumière dans le milieu. On retrouve ainsi la loi des sinus: \[ n_a~\mathbf{sin~}\alpha = n_b~\mathbf{sin~}\beta\]