"Sosa" est un terme fréquemment utilisé par les généalogistes, mais pratiquement ignoré du commun des mortels. De quoi s'agit-il ?

Chacun a été tenté de construire son arbre généalogique. Il se situe à la "racine" de l'arbre; son père et sa mère forment les deux premières "branches", les grands parents (paternels et maternels) ramifient chacune de ces deux en deux nouvelles, soit au total quatre nouvelles branches. Ensuite.. Mais on se décourage assez rapidement. En général, on n'a pas ou peu connu ses arrières-grands-parents; de plus on se rend compte que le travail deviendra rapidement insurmontable étant donné le nombre d'aïeux qui double à chaque nouvel étage.

Pourtant, les généalogistes ne sont pas découragés par l'ampleur de la tâche et ils effectuent de nombreuses recherches afin de compléter les branches de leur arbre. Comme les mots deviennent rapidement encombrants et difficilement compréhensibles (arrière-grand-mère paternelle) et tout simplement inadaptés, ils utilisent le terme mystérieux de "sosa" qu'ils complètent par un nombre.

Qu'est-ce que ce "sosa" ? Ce mot est tout simplement un nom de famille. Jérome de Sosa reprit un système de numérotation des ancêtres introduit en 1590 par un historien allemand, Michel Eyzinger. Ce moine espagnol popularisa cette numérotation et l'histoire retint son nom, probablement plus simple à prononcer que celui d'Eyzinger. Par la suite, cette méthode fut peaufinée, entre autres par Kekule, un chimiste réputé, généalogiste à ses heures.

La méthode est remarquablement simple.

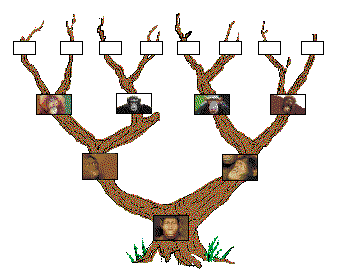On part de la racine de l'arbre (la personne dont on étudie la généalogie) et qu'on nomme d'un terme savant le "de cujus" auquel on attribue le nombre \(1\). Ensuite, on travaille par générations ascendantes: le père et la mère auxquels on attribue respectivement les nombres \(2\) et \(3\). On passe ensuite à la génération 2 (les 4 grands-parents) et on classe: d'abord le grand-père paternel et la grand-mère paternelle suivis du grand-père maternel et de la grand-mère maternelle; on leur attribue les nombres suivants: \(4, 5, 6\) et \(7\). Pour chacune de générations suivantes on procède d'une manière analogue.

Que les féministes se rassurent; si à chaque étape, les hommes précèdent les femmes, c'est que, dans notre civilisation, le nom de famille est transmis par le père. Certes, ce système patriarcal fait également l'objet de critiques; d'ailleurs dans certains pays (Espagne, Portugal entre autres) les deux patronymes sont transmis. Toutefois, il est exclu de continuer plus loin, sinon on en doublerait le nombre à chaque génération; par la suite, il faudrait faire un choix qui s'il était libre, engendrerait souvent pas mal de désaccords.

Voici donc comment sont numérotés les ancêtres jusqu'à la 4 ^e génération.

4	\(16\)	\(17\)	\(18\)	\(19\)	\(20\)	\(21\)	\(22\)	\(23\)	\(24\)	\(25\)	\(26\)	\(27\)	\(28\)	\(29\)	\(30\)	\(31\)
3	\(8\)		\(9\)		\(10\)		\(11\)		\(12\)		\(13\)		\(14\)		\(15\)
2	\(4\)				\(5\)				\(6\)				\(7\)
1	\(2\)								\(3\)
0	\(1\)

A chaque génération, le nombre de personnes double. A la 4 ^e génération, il y a 16 individus et à la 5 ^e il y en aura 32.

Si l'on estime qu'une génération correspond à 20 ans, ce qui est le cas presque partout dans le monde à l'exception des pays "riches", une personne aurait donc eu 32 (= 2 ⁵ ) ancêtres il y a 100 ans, 1024 (= 2 ¹⁰ ) il y a 200 ans, plus d'un million il y a 400 ans, plus d'un milliard il y a 600 ans, ...

Mais où allons nous ainsi ? On sait pourtant que la population n'a cessé de croître. Au début du 20e siècle, il y avait à peine plus de 2 milliards d'êtres humains; en 2000, il y en a plus de 6 milliards. Où est le paradoxe ? A plusieurs endroits. Tout d'abord, frères et sœurs ont les mêmes ascendants et il faut donc effectuer, à chaque génération, la division par le nombre moyen d'enfants (par couple) ayant vécu assez longtemps pour s'être reproduits. Ensuite, par le fait qu'on retrouve à certaines générations les mêmes personnes: dans le temps, les déplacements étaient fort réduits et il y avait pas mal de consanguinité. Bref, autant de facteurs qui expliquent ce paradoxe apparent.

Une petite question intéressante: combien y a-t-il d'individus au total jusqu'à la 4 ^e génération ? La réponse est évidente puisqu'on les a tous numérotés et qu'on s'est arrêté au n°31.

Mais on pourrait raisonner de manière plus intéressante et obtenir un résultat plus général.

Le problème est de calculer le nombre d'individus jusqu'à la n ^e génération qui est égal à:

\[ 1+2+4+...+2^n \] ce qui se généralise au calcul de : \[ 1+a+a^2+a^3+...+a^n \]

Si au lieu de "\(a\)" on avait écrit "\(r\)", on aurait immédiatement songer au calcul de la somme des \(n+1\) termes d'une suite géométrique de raison \(r\) dont le premier terme vaut \(1\). Au contraire, si on avait utilisé la lettre "\(x\)" au lieu de "\(a\)", on aurait reconnu une expression apparaissant dans les produits remarquables. Un bel exemple qui montre qu'il faut pouvoir se détacher des notations. Peu importe le sens de a !

Posons \(S=1+a+a^2+a^3+...+a^n\). En multipliant \(S\) par \((a-1)\), les simplifications vont en cascade et le résultat donne \(a^{n+1}-1\); on obtient ainsi la formule générale:

\[ 1+a+a^2+a^3+...+a^n =(a^{n+1}-1)/(a-1) \]

Dans l'exemple qui nous intéresse, \(a=2\) et la somme \(1+2+2^2+2^3+...+2^n\) vaut \(2^{n+1}-1\).

Revenons-en à cette numérotation.

Comme chaque individu possède exactement deux parents, il est évident qu'il serait plus adapté d'écrire ces nombres en système binaire. La transformation de nombres décimaux en nombres binaires est remarquablement simple, comme expliqué dans l'article sur la magie .

Pour faciliter la lecture, limitons-nous à la 3 ^e génération et traduisons donc le tableau précédent. Nous obtenons:

3	\(1000\)	\(1001\)	\(1010\)	\(1011\)	\(1100\)	\(1101\)	\(1110\)	\(1111\)
2	\(100\)		\(101\)		\(110\)		\(111\)
1	\(10\)				\(11\)
0	\(1\)

Quelques observations sautent aux yeux.

Dès la première génération, les hommes sont distingués des femmes; un homme est affecté d'un sosa se terminant par "\(0\)", une femme d'un sosa se terminant par "\(1\)" (les féministes sont rassurées !). Seule la racine de l'arbre, le sosa \(1\), peut représenter un être masculin ou féminin. Ce chiffre \(1\) qui se répercute à tous les étages au début de chacun des nombres binaires, n'apporte aucune information sur le sexe de la personne. Par contre, à partir du deuxième, tous les autres chiffres sont significatifs.

Un petit exemple: le sosa \(14\) correspond au nombre \(1110\). En ôtant le premier chiffre non significatif, il reste les chiffres \(110\) qui désignent respectivement une femme, une femme et un homme. Il s'agit donc du père de la mère de la mère du "de cujus", racine de l'arbre.

On remarque que la génération est tout simplement égale au nombre de chiffres binaires diminué d'une unité \(3\) pour le sosa \(14\) de l'exemple précédent).

Grâce à cette numérotation binaire, il est facile de savoir le nombre de changements de patronyme qui a été nécessaire pour arriver d'un individu au "de cujus". Un changement de patronyme correspond au mariage d'une femme, donc à la présence d'un "\(1\)"; il est donc, tout simplement, égal au nombre de chiffres binaires "\(1\)" contenu dans le numéro du sosa (compte non tenu du "\(1\)" initial).

Enfin, si l'on souhaite restreindre l'arbre à un autre individu, cela se fait très aisément à l'aide d'une simple substitution. Un exemple: l'arbre du sosa \(10\) s'obtiendra en prenant la partie supérieure à cet individu et en remplaçant partout le "\(10\)" initial par un "\(1\)".

\(10000\)	\(10001\)	\(10010\)	\(10011\)	\(10100\)	\(10101\)	\(100110\)	\(10111\)
\(1000\)		\(1001\)		\(1010\)		\(1011\)
\(100\)				\(101\)
\(10\)

devient

\(1000\)	\(1001\)	\(1010\)	\(1011\)	\(1100\)	\(1101\)	\(1110\)	\(1111\)
\(100\)		\(101\)		\(110\)		\(111\)
\(10\)				\(11\)
\(1\)