Introduction
Dans cet article, nous allons revenir sur différentes notions liées à la complexité amortie. Quelles sont les nouvelles questions qui émergent lorsqu’on étudie des algorithmes, ou plus spécifiquement des structures de données, sur un aspect plus dynamique. Dans ce cadre, nous ne nous intéresserons pas à une seule opération isolée, mais bien à une séquence d’opérations. Que peut-on dire du coût total de celles-ci et du temps amorti de chacune d’elles ? La complexité d’une opération, dans ce cadre, peut dépendre éventuellement de toutes les autres qui l’auront précédée et influencer celles qui suivront. Comment modéliser ce genre de problèmes, les étudier et définir des critères d’optimalité dans ce contexte ?
Nous commencerons par présenter les concepts fondamentaux de ce type de théorie en établissant les définitions usuelles avec la vue duale du problème. Afin de clarifier les propos, nous présenterons deux exemples simples, mais qui sont assez communs en informatique. Ensuite, nous nous pencherons sur une structure de données classique de ce domaine et qui présente des usages quelque peu "farfelus" mais des analyses de complexité particulièrement singulière. Finalement, nous présenterons brièvement le concept de stratégie sur une structure de données et les concepts d’optimalité qui y sont liés.
Malgré une présentation de problèmes très classiques et introductifs à cette matière. Cet article nécessite quand même d’avoir un certain bagage de connaissances en informatique théorique (surtout de l’algorithmique et de la programmation) et cela s’adresserait classiquement à des étudiants étant au moins en début de master.
Complexité amortie
Le point central qui caractérise la notion de complexité amortie est avant tout le fait que la complexité d’une opération (sur une structure de donnée ou l’exécution d’un algorithme) est évaluée au sein d’une séquence d’opérations. La complexité amortie est définie comme le coût total d’une opération au sein de la séquence, c’est-à-dire, que le coût amorti dépend non seulement de l’opération elle-même et qualifié de coût actuel, mais également des conséquences qu’elle pourrait avoir sur les opérations futures. En particulier, l’idée est de garantir le coût total sur l’entièreté de la séquence, tout en permettant à des opérations individuelles d’être plus coûteuse que le coût amorti.
On définit le coût amorti comme étant le coût total de la séquence d’opérations \(\sigma\) divisée par le nombre d’opérations effectuées, soit \(\text{total cost}(\sigma) / |\sigma|\). Autrement dit, le coût amorti d’une opération est le coût maximal de toutes les séquences d’opérations \(\sigma\) contenant celle-ci. En particulier, le pire cas pour une séquence de \(p\) opérations est toujours inférieure ou égale à \(p\) fois le pire cas de n’importe laquelle de ces opérations.
K-bit counter
L’exemple introductif par excellence des problèmes de complexité amortie est celui du K-bit counter. Il s’agit d’un problème dans lequel vous avez un compteur de \(K\) bits et sur lequel vous ne pouvez qu’incrémenter:
$$ b_{0} b_{1} ... b_{k - 1} $$L’algorithme pour incrémenter le compteur est le suivant (on flip tous les bits à \(1\) et dès qu’on tombe sur un \(0\), on le transforme en \(1\)):
def increment(counter):
k = len(counter)
t = k - 1
while counter[t] == 1:
counter[t] = 0
t -= 1
counter[t] = 1
Le pire cas correspond à la situation où le compteur n’est composé que de \(1\) ce qui donne du \(O(K)\). Évidemment, la majorité du temps cette complexité ne sera pas atteinte.
On revient au problème amorti. Quelle est la complexité d’incrémenter \(n\) fois ce compteur ? On sait que ce sera forcément inférieur à \(O(n K)\).
En réfléchissant un peu, on se rend compte que:
- Le bit en position \(k - 1\) sera flippé \(n\) fois
- Le bit en position \(k - 2\) sera flippé \(\frac{n}{2}\) fois
- Le bit en position \(k - i\) sera flippé \(\frac{n}{2^{i-1}}\) fois
Le temps total sera donc borné par:
$$ n + \frac{n}{2} + \frac{n}{4} + ... = \sum_{i=0}^{\log_2(k)} \frac{n}{2^{i-1}} = 2 n $$Pour obtenir le coût amorti, il suffit de diviser ce temps total (\(2n\)) par le nombre d'opérations (\(n\)) et on obtient que la complexité amortie est inférieure ou égale à \(2\).
Une question de budget
Un concept qui revient à maintes et maintes reprises dans les problèmes de complexité amortie est la notion de budget. L’idée consiste à dire qu’on attribue, à chaque opération, un certain budget. Si l’opération ne consomme pas tout son budget, alors elle crédite une "balance". Si une opération nécessite davantage de budget, elle peut alors puiser dans cette balance, en évitant qu’elle ne devienne négative. La question devient alors, quel est le budget minimal qu’il est suffisant d’attribuer afin de résoudre le problème ?
Un potentiel argument
Afin de déterminer quelle est la quantité minimale de budget nécessaire en vue de répondre à la problématique. On introduit une nouvelle notion qu'on qualifie de (fonction de) *potentiel*. La recherche de cette fonction de potentiel en elle-même est là où réside la plus grande partie de la difficulté de l'analyse amortie.
De manière générale, on définit la fonction de potentiel \(\Phi\) sur la "balance" comme le budget déjà disponible: \(\Phi(balance) = \text{budget total disponible}\).
$$ \text{actual cost}_t = \text{amortized cost}_t (\text{operation budget}) - ( \Phi(\text{balance}(t+1)) - \Phi(\text{balance}(t)) ) $$La logique étant que si l'on veut emprunter depuis la balance, le potentiel va diminuer. Et réciproquement, si nous n'avons pas besoin d'emprunter, on veut que le potentiel augmente.
Dans le cadre de notre compteur, la fonction de potentiel qui apparaît naturellement est le nombre de \(1\) présents dans celui-ci. En effet, on sait que chaque incrémentation va forcément transformer un \(0\) en \(1\) mais, le nombre de \(1\) à transformer en \(0\) dépend du nombre de ceux-ci.
Le *actual cost* vaut \(l\) parce que l'on sait qu'on va devoir flipper \(l\) uns. Le potentiel va alors perdre \(l - 1\) uns sur les \(k\) qui resteront mais, on va en rajouter \(1\) un. On se retrouve avec:
$$ \text{amortized cost} = l + (k + l - 1) - (k + 1) = 2 $$Pour être tout à fait complet, il faut bien comprendre que les relations présentées sont des égalités strictes. C'est-à-dire que sur un compteur quelconque initial, il faut prendre en compte le nombre de uns initiaux.
$$ \begin{align} & \sum \text{amortized cost over a sequence} = \sum \text{actual cost over that sequence} \\ & + \Phi(\text{balance(final situation)}) - \Phi(\text{balance(original situation)}) \\ & \leq \sum \text{actual cost over that sequence} + \Phi(\text{balance(original situation)}) \\ \end{align} $$Dynamic array
Maintenant que les principaux concepts ont été définis et que nous avons vu des éléments de cette logique adaptés à l’exemple du \(K\)-bit counter, nous pouvons également mentionner le cas classique du dynamic array que l’on retrouve dans de nombreux langages de programmation, sous les noms de vector, ArrayList ou List. Il s’agit du cas classique d’un tableau continu en mémoire qui s’étend dynamiquement au fur et à mesure des insertions.
Supposons que la taille de la structure de données double toutes les puissances de 2 éléments. Le coût de l’insertion est toujours d’au moins un, pour l’ajout du nouvel élément, et, dans le pire cas, le coût aura la taille des données déjà présentes qu’il faudra transférer au nouvel endroit.
$$ \begin{cases} C_{i} &= 1 + (i - 1) & \text{if \(i-1\) is a power of 2}\\ &= 1 & \text{otherwise} \end{cases} $$On se retrouve alors avec comme coût total: \(\sum_{i=1}^{n} C_{i} = n + \sum_{k=0}^{\lfloor{\log n}\rfloor} 2^{k} \leq n + 2n\) et donc un coût amorti de \(3\).
On peut se demander pourquoi le choix d’un facteur d’accroissement de 2 et pas un facteur quelconque. Tant qu’on alloue toujours davantage d’éléments que ceux initialement présents, il n’y aura pas de problème. On peut étudier l’évolution du coût amorti en fonction du facteur d’accroissement.
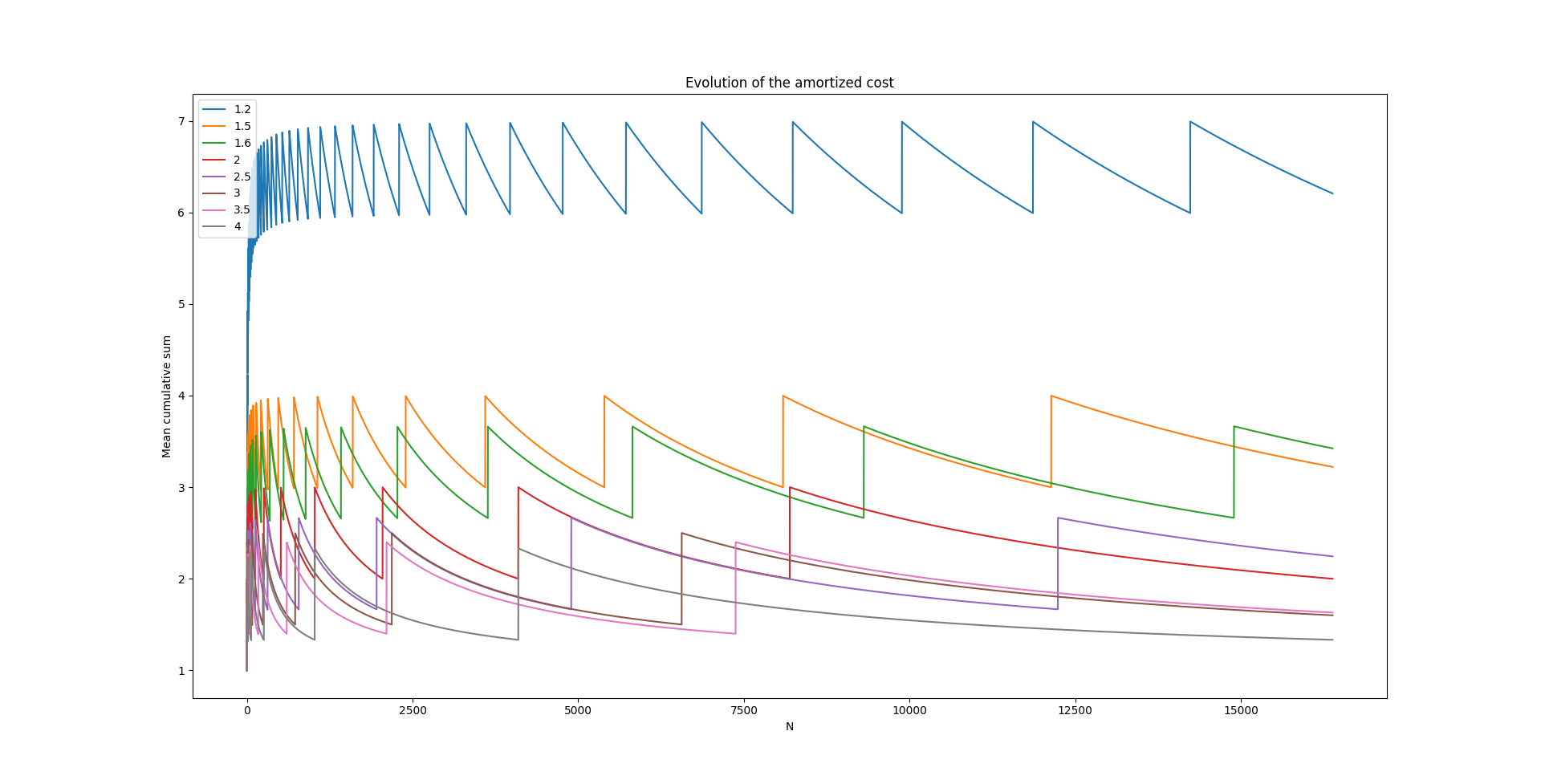
On voit (un peu difficilement) sur ce graphique, en rouge, la courbe qui correspond au facteur d'accroissement valant 2 et qui ne dépasse jamais 3. On observe également que, plus le facteur d'accroissement est élevé, plus le coût va tendre vers 1 et à l'inverse, moins on va réserver d'espace supplémentaire à chaque allocation, plus le coût va tendre vers \(n\) (le pire cas étant de ne réserver que \(n+1\) à chaque fois). Le gain devient de moins en moins intéressant plus le facteur d'accroissement est grand et il faudra alors opérer un choix sur la quantité de mémoire que nous sommes prêts à concéder (et éventuellement ne pas exploiter) et la complexité que l'on veut se permettre sur cette opération.
On peut également retomber sur ce résultat en invoquant le potentiel. On commence par définir deux quantités: \(size(L)\) qui correspond au nombre d'éléments dans \(L\) et \(capacity(L)\) qui est le nombre d'emplacements maximal que peut contenir \(L\). On définit le potentiel avec cette formule-ci:
$$ \Phi(L) = 2 * (size(L) - \frac{capacity(L)}{2}) = 2 * size(L) - capacity(L) \geq 0 $$On se retrouve avec soit:
- amortized cost (pas d'extension) = actual cost \( + (2 * size(L_{i}) - capacity(L_{i})) \) \( - (2 * size(L_{i-1}) - capacity(L_{i-1})) = 1 + (2 * i - k) - (2 * (i - 1) - k) = 3 \), vu que la capacité ne change pas.
- amortized cost (en cas d'extension) = actual cost \( + (2 * size(L_{i}) - capacity(L_{i})) \) \( - (2 * size(L_{i-1}) - capacity(L_{i-1})) = 1 + (2 * i - 2 * capacity(L_{i-1})) - (2 * (i - 1) - (i)) = 3 \), puisque c'est à l'insertion du \(i\) élément qu'on doit doubler la taille.
Disjoint-set
Maintenant que vous devriez avoir une première intuition de ce qu’est la complexité amortie. Il est tant de s’attaquer à un problème plus complexe !
Mon choix s’est porté sur la structure de données dénommée "disjoint set" de Galler et Fischer en 19641. En effet, elle est quelque peu "singulière" par les capacités qu’elle fournit, elle est également "optimale"2 et présente des complexités amusantes car peu classiques34.
La structure de données en elle-même fournit deux opérations sur des ensembles d’éléments:
- Find(x): détermine la classe d’équivalence d’un élément, cela retourne l’ensemble dans lequel l’élément se trouve (un même élément ne peut pas être présent dans plusieurs (sous-)ensembles).
- Union(X, Y): réunit deux classes d’équivalence en une seule, réalise l’union de deux ensembles.
Outre la pure satisfaction des délires d’informaticiens théoriques, cette structure possède plusieurs applications. Nous pouvons citer "Tarjan’s off-line LCA" (problème du plus petit ancêtre commun)5, "Robinson’s Unification" (ou la recherche du nombre de degrés de liberté dans l’instanciation de règles dans le système de type de Hindley-Milner)6, l’algorithme de percolation de Hoshen-Kopelman7, dans le traitement d’images8 et surtout ses connexions très profondes avec les problèmes de composantes connexes et d’optimalité dynamique.
C’est surtout sur ce dernier point que nous allons nous pencher avec, pour exemple, l’algorithme de Kruskal9, ou plus communément appelé "Arbre couvrant de poids minimal" (Minimum spanning tree). Pour rappel, l’algorithme est constructif, on rajoute petit à petit les arêtes de poids minimal si elles ne forment pas un cycle. Cette manière de procéder est qualifiée de gloutonne:
def Kruskal(G):
F = set()
disjoint_set = create_disjoint_set(G.vertices)
sorted_edges_by_weight = sort(G.edges)
for (u, v) in sorted_edges_by_weight:
if disjoint_set.find(u) != disjoint_set.find(v):
F = F | {(u, v)} | {(v, u)}
disjoint_set.union(disjoint_set.find(u), disjoint_set.find(v))
Galil et Ialiano ont proposé un résumé des structures de données et des algorithmes qui existaient en 1991 pour ce problème10. Nous allons nous intéresser à deux modèles de représentation distincts.
Sous formes de listes
Supposons l’ensemble des ensembles suivants (l’indice entre parenthèses représente l’indice du sous-ensemble):
$$ \{ \{4, 7\} ^{(1)}, \{1, 2, 5\} ^{(2)}, \{ 3, 9 \} ^{(3)}, \{ 6, 8 \} ^{(4)} \} $$Pour obtenir du \(O(1)\) sur l'opération de Find, on peut créer la table suivante:
| élément x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| indice de l’ensemble | 2 | 2 | 3 | 1 | 2 | 4 | 1 | 4 | 3 |
Parfait, la correspondance est directe, pas de soucis pour le Find.
Maintenant, comment réaliser l’opération Union et mettre à jour la structure de données ? Pour cela, il nous faut d’abord trouver un moyen de mettre à jour uniquement le plus petit ensemble des deux qui sera fusionné. En effet, si on met à jour le plus grand ensemble, on risque d’atteindre une complexité quadratique, alors qu’il y a moyen de faire mieux.
| indice de l’ensemble | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| nombre d’éléments | 2 | 3 | 2 | 2 |
| premier élément | 4 | 1 | 3 | 6 |
Il manque encore une information, comment trouver tous les éléments faisant partie d’un même ensemble à partir d’un élément de cet ensemble ? Et bien, il suffit de rajouter un pointeur vers l’élément suivant (avec "\" représentant la fin de la chaîne):
| élément x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| indice de l’ensemble | 2 | 2 | 3 | 1 | 2 | 4 | 1 | 4 | 3 |
| élément suivant de x | 2 | 5 | 9 | 7 | \ | 8 | \ | \ | \ |
La structure de données en elle-même n’est pas particulièrement élégante, mais répond à notre besoin. Elle peut être construite en temps linéaire et nécessite également un espace linéaire.
Le Find est en temps constant \(O(1)\) et Union(X, Y) est en \(O(min(|X|, |Y|))\).
Maintenant, qu'en est-il de la complexité amortie dans le cadre de l'algorithme de Kruskal ? Au départ, chaque nœud du graphe (au nombre de \(n\)) est mis dans un sous-ensemble différent. Dans le pire cas, on va devoir parcourir chacune des arêtes (au nombre de \(m\)), mais nous n'effectuerons l'opération Union au maximum que \(n-1\) fois puisque tous les éléments appartiendront éventuellement tous au même ensemble. La complexité de cet algorithme, outre le tri des arêtes qui peut éventuellement être linéaire) sera alors en \(O(|E| + |V| \log |V|)\).
L'argument est le suivant. Combien de fois un élément se verra changer l'ensemble auquel il appartient ? Il faut observer que, pour chaque élément, son ensemble associé ne change que lorsqu'il y a une Union avec son ensemble. Or ce dernier est fusionné avec un ensemble qui possède au moins la même taille, et ce, pour former un nouvel ensemble dont la taille sera au moins double (par rapport au plus petit). Donc, chaque élément verra l'ensemble auquel il appartient changer au maximum \(\log n\) fois.
Sous formes d’arbres
On peut également représenter ce problème sous la forme d’arbres auxquels on associe la racine à l’indice de l’ensemble associé.
D’une part, nous avons les singletons que nous représentons par un nœud unique (et donc à la racine) muni de l’ensemble associé. D’autre part, l’Union consiste simplement à adjoindre l’un des ensembles préexistants comme un simple enfant de l’autre.
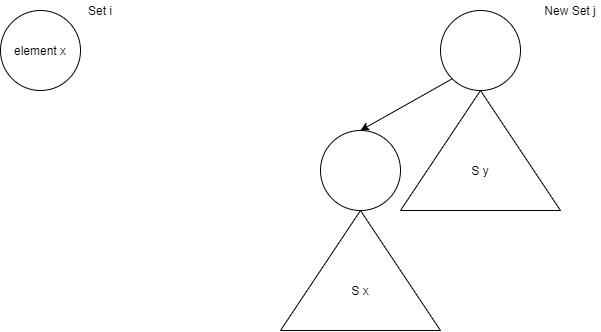
L'opération d'Union devient alors en temps constant alors que celle de Find ne l'est plus. À partir d'un élément, il faut remonter jusqu'à la source de l'arbre, ce qui est en \(O(\text{hauteur(arbre)})\). Remarquons également que nous n'avons pas apporté davantage de précision sur quel arbre devenait l'enfant de l'autre en cas d'union. En effet, on peut appliquer deux techniques simples, soit sur base du critère du nombre d'éléments présents dans l'arbre, soit sur base de la hauteur de l'arbre. Dans les deux cas, l'arbre le plus petit devient un des fils de l'autre. En pratique, cette hauteur de l'arbre peut être bornée par un argument similaire à celui précédemment mentionné pour les listes.
Seulement, nous sommes dans le cas d’analyse amortie. Pourquoi ne pas augmenter la complexité de l’opération Find actuelle à fin d’améliorer la complexité des suivantes ? Pour cela, on peut appliquer le principe de "Path Compression" de Tarjan4. C’est-à-dire, quand même temps qu’on recherche la racine de l’arbre pour l’élément, on met également à jour certains nœuds de l’arbre afin qu’ils aient la racine pour parent direct (cela peut s’effectuer en pratiquant deux parcours au lieu d’un seul).
Logarithme itéré
Il est alors possible de montrer que la complexité est en \(O(|E| \log^{*} |V|)\)3. Mais qu'est-ce donc ce \(\log^{*}\) ? Il s'agit du logarithme itéré, du nombre de fois qu'il faut appliquer l'opérateur \(\log\) à \(n\) afin que le résultat soit inférieur à 1.
$$ \log^{*} n = min\{i | log log ... log (n) \leq 1\} $$Il s’agit d’une opération qui croît de manière particulièrement lente:
| \(n\) | \(\log^{*} n\) |
|---|---|
| \((−\infty, 2^0]\) | 0 |
| \((1, 2^1]\) | 1 |
| \((2, 2^2]\) | 2 |
| \((4, 2^{4} = 2^{(2^2)}]\) | 3 |
| \((16, 2^{16} = 2^{(2^4)}]\) | 4 |
| \((65536, 2^{256} = 2^{(2^{16})}]\) | 5 |
Vu que la croissance obéit à une suite de puissances de 2, nous emprunterons par la suite la notation de Knuth pour les "up-arrow" (\(\uparrow\)). Il faudra lire: \(a \uparrow\uparrow b\) comme suit: \(a^{...^{a}}\) avec \(b\) mises en puissance de \(a\).
Outre les critères du nombre d’éléments ou de la taille des arbres, il existe un autre critère, le critère de "rang" (rank) qui représente une heuristique dans le but de déterminer la profondeur de l’arbre. Par défaut, les nœuds isolés sont de rang 0, lorsqu’on fusionne deux arbres de même rang, le nouveau rang est "l’ancien rang + 1". Remarquez que la notion de "rang" est bien une heuristique dans le cas du "path compression" puisque la taille réelle de l’arbre est constamment modifiée.
Il existe néanmoins trois propriétés liés à cette notion de rang:
- Rank(x) < Rank(parent(x)) à moins que parent(x) = x
- Le nombre de nœuds avec le rang \(r\) est \(\leq \frac{n}{2^{r}}\). En effet, pour chaque nœud de rang \(r\), il y a au moins \(2^{r} - 1\) autres nœuds. En effet, nous atteindrons le nombre maximal de nœuds de rang \(r\) lorsque chaque nœud de rang \(r\) sera la racine d'un sous-arbre composé d'au maximum \(2r\) nœuds.
- \(r \leq n\)
L'idée principale de la preuve consiste à prouver que chaque opération Find peut s'accompagner d'un budget d'au maximum \(\log^{*} n\) crédits.
Pour cela, on groupe les rangs \(r\) en \(\log^{*} n\) groupes avec le rang \(r\) qui appartient au \(G_{\log^{*}{r}}\).
| \(G_i\) | \(\{ ranks \}\) |
|---|---|
| \(G_0\) | Rank 0 |
| \(G_1\) | Rank 1 |
| \(G_2\) | Rank 2 |
| \(G_3\) | Rank 3, 4 |
| \(G_4\) | Rank 5, …, 16 |
| \(G_r\) | Rank Rank \(2\uparrow\uparrow (r-1) +1, ..., 2\uparrow\uparrow r\) |
Nous prenons également pour hypothèse que l'on emploie le crédit, associé au budget, uniquement si \(G(rank(x)) != G(rank(parent(x)))\), sinon on charge une unité de crédit.
Maintenant, comptons le nombre total de crédits associés au nœud \(x\). On sait qu'il est inférieur ou égale au nombre de rangs dans le groupe de \(x\). En effet, avec la compression du chemin, après avoir accumulé un crédit, on sait que le \(rank(parent(x))\) va augmenter (puisque les rangs sont en augmentation monotone jusqu'à la racine). Et le nœud \(x\) va arrêter d'accumuler du crédit jusqu'à ce que son rang soit le plus grand de son groupe.
Maintenant, prenons le groupe \(G_r\), le nombre de crédits de chaque élément de ce groupe sera borné par \(2\uparrow\uparrow r - 2\uparrow\uparrow (r-1)\). Or, si l'on pose que \(R = 2\uparrow\uparrow (r-1)\), et que l'on calcule le nombre d'éléments dans \(G_r\), on a:
$$ G_r \leq \frac{n}{2^{R+1}} + \frac{n}{2^{R+2}} + ... + \frac{n}{2^{2^{R}}} \leq \frac{2n}{2^{R+1}} = \frac{n}{2^{R}} $$Au final, le nombre de crédits détenu par un nœud de \(G_r \leq 2^{R}\) et l'on sait que le nombre de nœuds est borné par \(\frac{n}{2^{R}}\), le nombre total de crédit est donc \(G_r \leq 2^{R} \frac{n}{2^{R}} = n\). Par construction, nous avons au maximum \(\log^{*} n + 1\) groupes. Le coût total de l'opération est donc bel et bien \(O(|E| \log^{*} |V|)\).
Ackermann
Cette partie est très largement inspirée par le livre "Introduction to algorithms" de C.E. Leiserson, R.L. Rivest, Th. Cormen et C. Stein.12
Tarjan11 est même allé encore plus loin que cette complexité en \(\log^{*}\) ! Pour cela, il faut d'abord commencer par créer une nouvelle fonction, dite de "Ackermann". Elle consiste à généraliser le principe selon lequel l'exponentiation est à la multiplication ce que la multiplication est à l'addition. Elle est définie comme suit pour deux entiers \(m, n > 0\):
$$ A(m, n) = \begin{cases} n + 1 & \text{if \(m = 0\)}\\ A(m - 1, 1) & \text{if \(m > 0\) and \(n = 0\)}\\ A(m - 1, A(m, n-1) & \text{if \(m > 0\) and \(n > 0\)} \end{cases} $$Qu’on peut interpréter comme suit:
$$ A(m, n) = \begin{cases} n + 1 & \text{if \(m = 0\)}\\ A^{(n+1)}(m - 1, n) & \text{if \(m > 0\)}\\ \end{cases} $$Avec de nouveau la notation de fonction itérée telle que \(A^{(0)}(m - 1, n)=n\) et \(A^{i}(m - 1, n)=A(m - 1, A^{(i-1)}(m-1, n))\) pour \(i \geq 1\).
Mais ce qui nous intéresse réellement est de définir l'inverse, et notée \(\alpha(n)\), de la fonction \(A(m, n)\) comme suit:
$$ \alpha(n) = min\{k : A(k, 1) \geq n \} $$En pratique, la fonction d’Ackermann croît infiniment plus vite que la tour des puissances précédemment mentionnées et, de fait, son inverse croît encore plus lentement que le logarithme itéré.
| \(n\) | \(\alpha(n)\) |
|---|---|
| \([0, 2]\) | 0 |
| \((2, 4]\) | 1 |
| \((4, 8)\) | 2 |
| \((8, 2048]\) | 3 |
| \((2048, A(4, 1)]\) | 4 |
La démonstration est assez similaire à celle vue précédemment. On cherche à définir la fonction de potentiel suivante:
$$ \Phi(x) = \begin{cases} 0 & \text{if \(rank(x) = 0\)}\\ \alpha(n) rank(x) & \text{otherwise}\\ \end{cases} $$Pour cela, on a besoin de définir également les deux fonctions suivantes:
$$ \begin{align} & level(x) = max\{k: parent(rank(x)) \geq A(k, rank(x))\} \\ & iter(x) = max\{k: parent(rank(x)) \geq A^{(k)}(level(x), rank(x))\} \end{align} $$La fonction \(level\) représente la catégorie à laquelle le nœud appartient et \(iter\) est le plus grand nombre de fois qu'on peut appliquer de manière itéré la fonction d'Ackermann au rang du nœud afin de dépasser celui de son parent.
Le but du jeu est de prouver les deux relations suivantes:
$$ 0 \leq level(x) \lt \alpha(n) \\ 1 \leq iter(x) \leq rank(x) $$Pour la première relation, nous savons que pour la première inégalité, \(rank(parent(x)) \geq rank(x) + 1 = A(0, rank(x))\). Pour la seconde inégalité, il faut remarquer ceci: \(A(\alpha(n), rank(x)) \geq A(\alpha(n), 1) \geq n \gt rank(parent(x))\). En effet, la fonction d'Ackermann et son inverse s'annule pour la valeur de l'itération nécessaire et par construction, le rang ne peut pas être supérieur au nombre de nœuds dans l'arbre.
Pour la seconde relation, nous avons, par construction de la fonction \(iter\), que \(rank(parent(x)) \geq A^{(k)}(level(x), rank(x)) = A^{(1)}(level(x), rank(x))\) et donc que \(1 \leq iter(x)\). Pour la seconde inégalité, nous avons que \(A^{(rank(x) + 1)}(level(x), rank(x)) = A(level(x) +1, rank(x)) \geq rank(parent(x))\), ce qui implique l'autre borne.
Nous y sommes presque ! On doit encore définir la fonction de potentiel associée à chaque nœud après l'exécution de \(q\) opérations.
$$ \Phi_q(x) = \begin{cases} \alpha(n) rank(x) & \text{if \(rank(x) = 0\) or \(x\) is root}\\ (\alpha(n) - level(x)) rank(x) - iter(x) & \text{otherwise}\\ \end{cases} $$Ce qui est borné par: \(0 \leq \Phi_q(x) \leq \alpha(n) rank(x)\), il suffit de remplacer les bornes dans les équations pour s'en rendre compte, en capturant bien la logique que le rang des parents ne fait qu'augmenter avec le temps, ce qui fait que pour que \(iter(x)\) diminue, \(level(x)\) doit augmenter. Par contre, si \(level(x)\) reste identique, alors \(iter(x)\) doit soit augmenter soit rester le même.
On y est presque, il ne reste qu'à se demander comment le potentiel varie et dans quelle mesure. Lorsqu'on effectue un Find, on a le potentiel qui diminue avec \(\Phi_q(x) \leq \Phi_{q-1}(x) - 1\), vu que si le \(level(x)\) reste constant, \(iter(x)\) augmente d'au maximum \(1\). Par contre, si \(level(x)\) augmente (d'au moins \(1\)), \(iter(x)\) ne peut diminuer qu'au maximum de \(rank(x)-1\). Or, par définition de notre fonction de potentiel, la perte est nette et inférieure à \(1\).
Ici, on a des bornes sur le coût lié à la différence de potentiel, mais il reste à prendre en compte le coût de l'opération, l'*actual cost*. Dans le cas d'une Union, l'opération est en \(O(1)\) auquel il faut adjoindre l'augmentation de potentiel lié à l'augmentation de rang éventuel de la nouvelle racine de l'arbre. Or, par définition de la fonction de potentiel, l'augmentation est bornée par \(O(\alpha(n))\). Le coût amorti de l'opération au final est en \(O(1) + O(\alpha(n))\).
Pour le Find, on va devoir remonter la chaîne jusqu'à arriver au parent, posons qu'on ait traversé \(s\) nœuds. Or, lors de la compression, au moins \(max(0, s- (\alpha(n)+2))\) nœuds verront leur potentiel diminuer d'au moins \(1\). On retrouve un argument équivalent à celui qu'on avait employé pour le logarithme itéré, les nœuds qui ne changent pas de potentiels sont, outre la racine et les feuilles, les derniers nœuds marquant la limite d'un \(level\). Or, on a \(\alpha(n)\) niveaux qui contiennent au moins un parent chacun dans la même catégorie. On se retrouve avec une complexité en \(O(s) - max(0, s - (\alpha(n) + 2)) = O(\alpha(n))\).
Au final, l'argument que nous avons effectué porte sur la considération de la situation d'un nœud dans l'arbre, mais tous les nœuds obéissent à cette même logique. Si on additionne le coût total, on tombe sur la complexité en: \(O(|E| \alpha(|V|))\).
- GALLER, Bernard A. et FISHER, Michael J. An improved equivalence algorithm. Communications of the ACM, 1964, vol. 7, no 5, p. 301–303.↩
- FREDMAN, Michael et SAKS, Michael. The cell probe complexity of dynamic data structures. In : Proceedings of the twenty-first annual ACM symposium on Theory of computing. 1989. p. 345–354.↩
- HOPCROFT, John E.. et ULLMAN, Jeffrey D.. . Set merging algorithms. SIAM Journal on Computing, 1973, vol. 2, no 4, p. 294–303.↩
- TARJAN, Robert Endre. A class of algorithms which require nonlinear time to maintain disjoint sets. Journal of computer and system sciences, 1979, vol. 18, no 2, p. 110–127.↩
- GABOW, Harold N. et TARJAN, Robert Endre. A linear-time algorithm for a special case of disjoint set union. Journal of computer and system sciences, 1985, vol. 30, no 2, p. 209–221.↩
- MILNER, Robin. A theory of type polymorphism in programming. Journal of computer and system sciences, 1978, vol. 17, no 3, p. 348–375.↩
- HOSHEN, Joseph et KOPELMAN, Raoul. Percolation and cluster distribution. I. Cluster multiple labeling technique and critical concentration algorithm. Physical Review B, 1976, vol. 14, no 8, p. 3438.↩
- FIORIO, Christophe et GUSTEDT, Jens. Two linear time union-find strategies for image processing. Theoretical Computer Science, 1996, vol. 154, no 2, p. 165–181.↩
- KRUSKAL, Joseph B. On the shortest spanning subtree of a graph and the traveling salesman problem. Proceedings of the American Mathematical society, 1956, vol. 7, no 1, p. 48–50.↩
- GALIL, Zvi et ITALIANO, Giuseppe F. Data structures and algorithms for disjoint set union problems. ACM Computing Surveys (CSUR), 1991, vol. 23, no 3, p. 319–344.↩
- TARJAN, Robert Endre. Efficiency of a good but not linear set union algorithm. Journal of the ACM (JACM), 1975, vol. 22, no 2, p. 215–225.↩
- LEISERSON, Charles Eric, RIVEST, Ronald L., CORMEN, Thomas H., et al. Introduction to algorithms. MIT press, 1994.↩
Move to front
Ouf, nous en avons terminé avec l’analyse du "disjoint-set". Malgré des concepts assez simples, la réflexion peut être poussée particulièrement loin et elle peut mener à des démonstrations suffisamment élégantes et "simples" malgré leur complexité intrinsèque. Heureusement pour nous, nous allons nous intéresser à un tout autre sujet qui sera moins "prise de tête", mais qui est fortement lié aux outils et concepts vus précédemment.
L’analyse compétitive, ou competitive analysis, est une étude de complexité algorithmique introduite par Daniel Sleator et Robert Tarjan1 au début des années 80. Elle mesure la qualité d’un algorithme qualifié de on-line en le comparant à une version dite off-line. Un algorithme est on-line s’il permet de répondre à une séquence de requêtes, une à la fois, et sans connaissances des opérations futures qui seront demandées. À l’inverse, un off-line possède cette information future et peut donc potentiellement prendre une meilleure décision à l’instant \(T\).
Avec l’idée que la version off-line est d’autant plus optimale que sa complexité totale (pour effectuer toutes les requêtes) est minimale pour toute séquence donnée et sera notée \(C_{OPT}\) (pour cost optimal). Pour la version on-line, la définition d’optimalité diffère un peu et est centrée autour du concept de c-compétitivité (ou c-competitive). Un algorithme on-line est dit c-compétitif si le coût total nécessaire pour desservir une séquence de requêtes est au maximum \(c\) fois le coût pour servir la même séquence mais cette fois-ci avec une version off-line (optimale). En d'autres termes, étant donné un algorithme \(\mathscr{A}\), une séquence \(\sigma\), une constante \(d\) et ce facteur \(c\), on atteint l'optimalité si:
$$ C_{\mathscr{A}}(\sigma) \leq c C_{OPT}(\sigma) + d $$Attention que ce n’est pas le seul type d’étude qui peut être mené sur les algorithmes on-line, il existe la bien-nommée analyse distribuée (ou distributional analysis ou encore average-case analysis). Comme son nom l’indique, le but est d’étudier le coût espéré (dans le sens de l’espérance statistique) nécessaire afin de répondre à une série de requêtes (non-connues à l’avance) et soumises à des hypothèses de distribution telles que les requêtes de type \(k\) ont la probabilité \(p_{k}\) d'apparaître peu importe les requêtes précédentes ou futures, etc … Ceci est généralement vu comme une notion moins forte que l’analyse compétitive.
L’un des exemples phares de l’analyse compétitive est l’étude de la stratégie move-to-front (MTF) pour l’accès et la mise à jour de listes simplement ou doublement liées. L’algorithme doit répondre à une série de requêtes qui consiste à parcourir la liste afin de trouver l’élément désiré. Seulement, afin de minimiser la coût total, l’algorithme a le droit de réorganiser la liste en échangeant les éléments de place. Le MTF consiste donc à déplacer le dernier élément accédé en tête de liste, avec l’espoir qu’on sera davantage susceptible de redemander ces éléments récemment accédés. En pratique et en théorie2, les performances sont époustouflantes et à seulement un facteur \(2\) par rapport au coût optimal3, et même qu’il n’existe pas d’algorithmes non-déterministes capables de faire mieux1 (s’ils sont non-déterministes, le facteur \(2\) peut légèrement être diminué45).
Retentons de démontrer le résultat de Sleator et Tarjan. Tout d’abord, il faut définir l’opération \(Find(x)\) comme étant la requête correspondant au fait de trouver l’élément \(x\) dans la liste. Le coût de cette opération est définie par:
- Le nombre d'éléments devant \(x\) (avant les transpositions).
- Le coût des transpositions.
En pratique, le déplacement de l’élément vers la tête de la liste est "gratuit" puisqu’en temps constant, mais cette hypothèse n’est même pas nécessaire au résultat.
On cherche à prouver que:
$$ C_{MTF}(\sigma) \leq 2 C_{OPT}(\sigma) $$Pour cela, il suffit de prouver que le \(\text{amortized cost}_{MTF}(i) \leq \text{amortized cost}_{OPT}(i)\) pour toute opération \(i\).
Représentons la situation pour la liste \(L\), à l'opération \(i\) avec la stratégie MTF:
| \(L_{i - 1}\) | \(A \cup B\) | \(x\) | \(C \cup D\) |
| \(L_{i}\) | \(x\) | \(A \cup B \cup C \cup D\) |
Alors que pour la stratégie OPT, on a:
| \(L^{*}_{i - 1}\) | \(A \cup C\) | \(x\) | \(B \cup D\) |
Avec:
- \(A\) l'ensemble des éléments dans \(L_{i - 1}\) et \(L^{*}_{i - 1}\) avant \(x\).
- \(B\) l'ensemble des éléments avant \(x\) dans \(L_{i - 1}\) mais après \(x\) dans \(L^{*}_{i - 1}\).
- \(C\) l'ensemble des éléments après \(x\) dans \(L_{i - 1}\) mais avant \(x\) dans \(L^{*}_{i - 1}\).
- \(D\) l'ensemble des éléments dans \(L_{i - 1}\) et \(L^{*}_{i - 1}\) après \(x\).
Le \(\text{actual cost}_{MTF}(i)\) est donc égale à \(|A| + |B|\) puisqu'il faut traverser tous les éléments de \(A\) et \(B\) dans \(L_{i - 1}\). Mais, il manque la composante relative aux inversions. Pour cela, on définit la fonction de potentiel suivante:
$$ \Phi(L) = \text{nombre d'inversions (définit comme la paire (x, y) où x apparaît devant y dans l'un, mais y avant x dans l'autre) entre MTF L et OPT L*} $$Supposons que dans ce cas-là, la stratégie optimale ne modifie pas l'état de la liste actuelle. On se retrouverait avec \(L^{*}_{i - 1} = L^{*}_{i}\) et donc que:
\(\Delta \Phi = - |B| + |A|\)
puisque \(B\) est maintenant à la bonne position alors que \(A\) ne l'est pas.
Maintenant, supposons, sans pertes de généralité, que la stratégie optimale déplace l'élément \(x\) de \(K\) positions vers la gauche. Alors, on aurait eu: \(\Delta \Phi \leq - |B| + |A| + K\).
Maintenant, quel est le coût amorti ?
$$ \begin{aligned} \text{amortized cost}_{MTF}(i) &= \text{actual cost}_{MTF}(i) + \Delta \Phi_{i} \\ \text{amortized cost}_{MTF}(i) &\leq |A| + |B| - |B| + |A| + K \\ \text{amortized cost}_{MTF}(i) &\leq 2 |A|+ K \\ \end{aligned} $$Et quand est-il de l'\(\text{actual cost}_{OPT}(i)\) ? Il vaut \(|A| + |C|\) puisqu'il faut traverser tous les éléments de \(A\) et \(C\) dans \(L^{*}_{i - 1}\) auquel il faut adjoindre le coût des \(K\) transpositions. On a donc que: \(\text{actual cost}_{OPT}(i) = |A| + |C| + K\), et en particulier que:
$$ \text{actual cost}_{OPT}(i) \geq |A| + K $$Il ne reste alors qu’à effectuer le rapport des deux:
$$ \frac{\text{amortized cost}_{MTF}(i)}{\text{actual cost}_{OPT}(i)} = \frac{\leq 2 |A|+ K}{\geq |A| + K} \leq 2 $$Personnellement, je trouve la démonstration particulièrement élégante tant elle arrive à capturer toute l’essence de ces concepts, sans rentrer dans aucun détail technique malgré un théorème particulièrement puissant. Ce type de démonstrations est proche de ce que l’on retrouve dans les notions d'obliviousness où on ne fait aucune hypothèse qui n’a d’influence sur les conclusions. Ce type de démonstrations est souvent mise en évidence puisqu’il présente le maximum d’applicabilités.
Maintenant que vous avez vu ce résultat, vous allez sûrement vous poser de nombreuses questions sur ce qu’ils se passent si on emploie d’autres stratégies telles que la transposition (échange de l’élément trouvé avec son prédécesseur) et le comptage (la liste reste triée sur base du nombre d’accès aux éléments)6. Quel est le meilleur algorithme off-line à ce problème6 ? Qu’en est-il des autres structures de données comme les arbres ? Il faut savoir que la conjecture reste ouverte pour le cas dynamique (dynamic optimality conjecture) mais le problème est résolu par les splay-trees pour le cas statique (où on interdit la modification de la structure après sa construction)7.
- SLEATOR, Daniel D. et TARJAN, Robert E. Amortized efficiency of list update and paging rules. Communications of the ACM, 1985, vol. 28, no 2, p. 202–208.↩
- GONNET, Gaston H., MUNRO, J. Ian, et SUWANDA, Hendra. Exegesis of self-organizing linear search. SIAM Journal on Computing, 1981, vol. 10, no 3, p. 613–637.↩
- BENTLEY, Jon L. et MCGEOCH, Catherine C. Amortized analyses of self-organizing sequential search heuristics. Communications of the ACM, 1985, vol. 28, no 4, p. 404–411.↩
- IRANI, Sandy. Two results on the list update problem. Information Processing Letters, 1991, vol. 38, no 6, p. 301–306.↩
- BEN-DAVID, Shai, BORODIN, Allan, KARP, Richard, et al. On the power of randomization in on-line algorithms. Algorithmica, 1994, vol. 11, no 1, p. 2–14.↩
- BENTLEY, Jon Louis et MCGEOCH, Catherine Cole. Worst-Case Analyses of Self-Organizing Sequential Search Heuristics. CARNEGIE-MELLON UNIV PITTSBURGH PA DEPT OF COMPUTER SCIENCE, 1983.↩
- SLEATOR, Daniel Dominic et TARJAN, Robert Endre. Self-adjusting binary search trees. Journal of the ACM (JACM), 1985, vol. 32, no 3, p. 652–686.↩
Dans cet article, nous avons tenté de présenter brièvement ce très vaste sujet que représente la complexité amortie. Nous sommes revenus sur une sélection de problèmes qui illustrent assez bien ces concepts et mettent en évidence les questions que l’on peut se poser dans ce cadre. Nous avons vu comment on peut faire pour redéfinir les concepts de complexité afin d’intégrer l’impact des opérations sur celles qui suivent ou qui ont précédé. Comment en étudiant une séquence d’opérations, on peut se poser de nouvelles questions telles que la réorganisation dynamique de structures de données et quelles stratégies adaptées dans ces situations. Ce genre de résultat joue un rôle capital dans la vie de tous les jours et possède de nombreuses répercussions dans d’autres champs de l’informatique (notamment les structures de données relatives aux modèles de calcul en external memory).
Je ne peux malheureusement recommander de livres spécifiquement dédiés à ce champ de recherche. Il est d’usage de commencer l’écriture d’un livre lorsque le domaine étudié arrive à sa fin, que les principales conjectures ont été résolues, ou qu’on ait un recul suffisant sur ces connaissances. En l’occurrence, ce domaine est encore fort actif et la conjecture de "dynamic optimality on trees" est toujours ouverte. Néanmoins, comme d’habitude, le livre "Introduction to algorithms" de Cormen et al.1, dans son immensité, aborde également en partie cette thématique et présente d’autres structures de données dans ce canevas. Pour le moment, il faut se contenter de lire les articles de notre Dieu à tous, Robert Tarjan, et de tous les autres grands noms de ce domaine, nous penserons à Daniel Sleator, Michael Fredman, Bernard Chazelle (❤), Gerth Brodal, mais nous aurions pu en citer tant d’autres.
- CORMEN, Thomas H., LEISERSON, Charles E., RIVEST, Ronald L., et al. Introduction to algorithms. MIT press, 2009.↩