Introduction

Depuis longtemps, les gens se demandent comment résoudre des problèmes, s’il n’est pas possible de les résoudre de manière plus efficace, comment mieux exploiter des ressources pour arriver aux mêmes résultats ou bien encore quelles sont les limites inhérentes à ces problèmes. Dans cet article, nous allons revenir sur des concepts de base liés à la complexité, en tentant de dresser un portrait suffisamment global pour voir quelle est la science sous-jacente, les questions qu’on peut se poser en formulant ce concept. Cet article ne fait que survoler ce très vaste domaine et propose juste des clefs de compréhension afin de mieux concevoir ces problématiques, et ainsi mieux les étudier ou les formuler. Ces concepts peuvent s’avérer très utiles, au quotidien, lorsqu’un développeur s’intéresse à l’efficacité de sa solution ou qu’il doit régler des problèmes liés à la mise en production et une quantité inattendue de données.

Cet article se veut purement théorique et nécessite quand même un petit bagage scientifique, il est préférable d’avoir des connaissances de bases en informatique théorique (un peu d’algorithmique et de programmation) et cela s’adresserait donc à des étudiants étant au moins au milieu d’un bachelier (niveau licence pour nos amis français).

Définitions

Mais qu’est-ce donc que la complexité ? Il est coutumier de commencer toute présentation d’un concept par une définition issue du dictionnaire. Donc, faisons différemment et préférons l’approche didactique en mettant en relief les caractères distinctifs du concept !

La complexité en elle-même n’a que peu de sens, c’est une caractérisation de ce qui est qualifié de “complexe” par le sens commun. “Aller sur Mars” est très complexe mais “faire de la couture” l’est nettement moins. Et pourtant, rares sont ceux capables de coudre. Ce concept nécessite souvent une base de comparaison par rapport à un objet de même nature qui l’est davantage ou moins. Il est peu rigoureux d’annoncer quelque chose comme difficile ou simple sans fournir des justificatifs par rapport à des problèmes précédemment rencontrés ou communément acceptés. Il y a un doux mélange de raisons objectives et subjectives pour lesquelles on estime une tâche plus dure qu’une autre, que ce soit par les ressources que cela demande dans l’absolu (aller sur Mars) et la perception que l’on possède du problème (si je suis déjà couturier professionnel).

La complexité cherche donc à déterminer comment on peut définir à quel point une tâche est complexe.

En Sciences, on essaye d’éviter au maximum l’aspect subjectif et on tente de trouver une approche sur laquelle tout le monde peut se baser, la plus objective possible et éventuellement quantifiable. Prenons, le cas d’un jeu de cartes, chercher l’as de trèfle dans le paquet est intuitivement plus simple que de trier le paquet par valeur et par symbole, bien que le nombre de cartes est le même dans les deux situations. Ce qui soutient cette idée, c’est qu’il suffit de parcourir toutes les cartes jusqu’à tomber potentiellement sur l’as de trèfle alors que, pour trier, on va sans doute parcourir plusieurs fois le paquet et échanger la position de nombreuses cartes.

En cherchant à rationaliser le problème, on se rend compte que le nombre de ressources demandées pour effectuer ces tâches sont différentes, que ce soit dans le nombre de cartes qu’il faut regarder pour pouvoir répondre à ces questions, le nombre de manipulations entre les mains ou encore le nombre de cartes qu’il faut échanger de places. Et on peut se demander à quel point ces observations auraient été similaires avec seulement 2 cartes ou bien 3 paquets.

La complexité peut donc varier en fonction de la taille du problème, ou selon le critère qu’on étudie, et ce, pour une même tâche.

Seulement, les résultats qu’on pourrait obtenir avec le jeu de cartes pourraient difficilement être transposés à d’autres problèmes, tels que la résolution d’un système d’équations. Le problème de fond est qu’il est difficile d’exprimer ou de comparer la complexité de ces tâches spécifiques par rapport à des problèmes plus génériques. Il faudrait pouvoir définir un modèle, un ensemble de règles, tel qu’on puisse exprimer tous ces problèmes dans un même langage, qui permettrait alors plus facilement de les analyser et de les comparer. L’avancée majeure dans le domaine a été les résultats liés à la “Thèse de Church-Turing” ¹² et du problème de la décision (Entscheidungsproblem) au milieu des années 30 et qui s’est étendu pendant une dizaine d’années. Les très nombreux résultats issus de ces travaux dépassent très largement le contenu de cet article, mais celui qui nous intéresse est le suivant:

“Il est possible d’exprimer, par un ensemble de règles de calcul, tout ce qui est calculable en suivant un traitement systématique, un algorithme.”. Réciproquement, on définit ce qui est calculable comme étant tout ce qui peut s’exprimer aux travers de ces règles de calcul, en les appliquant selon un ordre précis, un algorithme.

C’est le problème de ce genre de résultats, ils apportent davantage de questions qu’ils n’en résolvent … Autrement dit, il existe des problèmes qui sont dits “calculables”, où il est possible de répondre à la question qui est posée en un nombre fini de ressources (et donc qu’il existe des problèmes qu’on ne peut résoudre et dits incalculables, peu importe le temps qu’on y consacre) - et la question de la calculabilité mériterait son propre article en lui-même. Et ces problèmes “calculables” peuvent tous être exprimés dans un langage - ensemble (fini) de règles de calcul - commun, et ce, par un système qui peut être automatisé, il suffit d’“appliquer les règles”. Ces règles se voulant le plus simple possible, elles peuvent se traduire par des actions telles que “ajouter 1 au nombre actuel”.

Il y a donc une relation très forte entre ce qu’on définit comme étant calculable et l’ensemble des règles de calcul que l’on choisit. La réciproque n’étant pas forcément uniquement, l’ensemble des problèmes, que l’on peut résoudre, peut correspondre à plusieurs ensembles de règles de calcul différents. Le résultat de la Thèse de Church-Turing était extrêmement fort parce qu’il montrait qu’on était capable d’exprimer une bonne partie des problèmes mathématiques sous la forme de questions que l’on était capable de résoudre, et ce, avec des règles relativement simples.

Pour résumer, la complexité s’intéresse à la définition et la quantification de la difficulté des tâches. Ces dernières sont exprimées par un ensemble de règles de calcul, opérations élémentaires ; plus il faut appliquer de règles, plus la tâche est complexe. La taille du problème a donc une relation très forte avec la complexité puisqu’il faudra sans doute appliquer davantage de règles pour arriver au même résultat. Également en fonction d’une ou des règles que l’on considère, la complexité peut également varier, et ce, pour un même problème.

Modèles de calcul

Simultanément à la preuve de l’existence de règles de calcul, sont apparus des formalisations mathématiques de ce que peut être une méthode de calcul. L’un des grands résultats associés à la thèse de Church-Turing est l’équivalence entre 3 modèles de règles calculs : le lambda calculus, les fonctions récursivement énumérables, et la fameuse “Machine de Turing” ¹. L’avantage de ce dernier modèle de calcul, par rapport aux deux précédents, était qu’il offrait une abstraction beaucoup plus simple à concevoir pour l’esprit et qu’il va connaître un ancrage dans le monde réel par la construction de machines physiques. Il est intuitivement plus simple d’imaginer des problèmes dans ce nouvel environnement que dans des formalismes mathématiques existants préalablement. Son usage sera soutenu par la preuve d’universalité qui sous-tend qu’il est possible d’exprimer n’importe quel problème calculable dans celui-ci. Autrement dit, l’ensemble de tous les problèmes calculables peut être exprimé par un seul modèle de calcul, un ensemble de règles unique sur lequel tout le monde peut s’accorder.

Ce qu’il faut bien comprendre :

• Le choix des règles de calculs n’est pas unique et que, en théorie, tous ces choix sont équivalents entre eux (à condition qu’ils respectent de très nombreuses propriétés - d’être universelles). Les machines actuelles sur lesquelles on calcule la complexité des programmes n’ont plus grand chose à voir avec la Machine de Turing, mais possèdent toujours la même puissance de calcul, elles peuvent exprimer les mêmes problèmes.
• Lorsque l’on parle de machine ou de modèle de calcul, ce sont des pures conceptions de l’esprit, mais qui possèdent une grande puissance mathématique et qui peuvent éventuellement être représentées dans le monde physique.
• La notion de puissance de calcul, de la calculabilité, est très liée à la définition du modèle de calcul. Un exemple est le modèle de calcul préféré d’Euclide : “La construction à la règle et le compas”, dans lequel on peut résoudre des équations du second degré, mais où l’on sait également qu’il n’est pas possible de résoudre différents problèmes (la duplication du cube, la trisection de l’angle, la quadrature du cercle, …). Il faut donc pouvoir montrer que deux modèles de calculs sont équivalents, que l’on est capable d’exprimer tous les problèmes d’un modèle avec l’autre et réciproquement.
• Toute complexité est exprimée par rapport à un modèle de calcul et donc qu’elle peut être exprimée selon un autre à condition de prendre en considération la conversion entre les deux modèles. Intuitivement, on peut considérer la multiplication comme une seule opération ou de nombreuses additions, par exemple.

Actuellement, on emploie essentiellement un ensemble de règles, une machine qualifiée de “RAM”² (pour machine à accès aléatoire en mémoire). Elle se rapproche conceptuellement d’une perception à haut niveau du fonctionnement d’un ordinateur, de toutes les primitives que l’on peut retrouver dans les langages de programmation actuels. On peut stocker ou lire des nombres n’importe où, les additionner ou soustraire ainsi qu’effectuer différentes opérations en fonction de la valeur d’un nombre (branchement conditionnel); et on associe à chacune de ces opérations un temps constant. Elle a l’avantage de proposer une certaine simplicité tant dans sa définition que dans son abstraction mentale et est devenue, de facto, un standard pour exprimer la complexité des problèmes (et sera implicitement employée pour notre cas d’étude plus bas).

Notations

Une fois qu’on a défini une machine de calcul - un ensemble des règles de calcul que l’on s’autorise - on peut se demander quels sont les problèmes que l’on peut résoudre, quel est le nombre minimal de règles qu’il faut appliquer pour répondre à un certain problème ou, plus simplement, comment fournir une solution. D’un point de vue historique, c’est l’inverse qui s’est produit, on a d’abord trouvé des manières de résoudre des problèmes et puis on a cherché à avoir un formalisme dans des modèles de calcul.

Laissons la question de la calculabilité de côté et attardons nous sur l’aspect lié à la complexité. Il faut d’abord observer que la complexité est généralement liée à la taille de l’entrée, que l’on dénotera \(n\) par la suite, chercher une aiguille toute seule dans une boîte est plus simple que de chercher dans toute une botte de foin. On essaye donc d’associer une fonction à la complexité d’un problème en fonction de la taille de l’entrée. Naturellement, plus la taille du problème sera grande, plus sa complexité sera élevée (trier un paquet de cartes est plus compliqué que de ne trier que 3 cartes). Cela offre l’avantage de pouvoir comparer deux algorithmes, soit pour une même taille de données, soit pour le comportement général de ces complexités et sur la manière dont elles évoluent en fonction de la taille de l’entrée. En pratique, on connaît rarement la taille des données en entrée et on préférera étudier la manière dont la fonction grandit, mais nous reviendrons sur cet aspect, plus loin.

Pour évaluer l’efficacité d’un algorithme, on le caractérise par un ordre d’accroissement. L’idée est que lorsque la taille de l’entrée devient suffisamment grande, on parle de comportement asymptotique, seuls les termes de plus grands ordres de la fonction vont demeurer. Si mon algorithme avait une complexité de type : \(f(x) = x^2 + 1\), le terme \( + 1\) devient négligeable par rapport à \(x^2\), et l’on dira qu’il est quadratique. Cela offre trois avantages :

• Il est plus simple de raisonner avec des ordres de grandeur pour pouvoir les comparer, plus de précisions n’apporte que peu d’intérêt dans ce type d’étude.
• Même si on est capable de fournir une fonction très précise de la complexité d’un algorithme, l’effort en vaut rarement la chandelle, car tant les facteurs multiplicatifs des termes que ceux d’ordres inférieurs se feront de toute façon dominés par les effets liés à l’augmentation de la taille.
• Le seul intérêt des analyses détaillées apparaît lorsqu’il existe plusieurs algorithmes qui possèdent le même comportement général et que l’on souhaite les comparer plus finement. Mais, malheureusement, généralement, les modèles de calcul sont des abstractions de la réalité et les résultats théoriques que l’on pourrait obtenir pourraient s’avérer loin des performances réellement observées.

Dans l’idée de ne garder que les ordres de grandeur, on introduit les notations suivantes pour décrire les comportements des fonctions. - La notation la plus connue, la notation dite “grand O” \(O(.)\):

$$O(g(n)) = \{ f(n) | \exists c > 0, \exists n_{0}, \forall n \geq n_{0}, \quad 0 \leq f(n) \leq c g(n) \}$$

C’est une définition très barbare qui exprime l’idée que la complexité qui nous intéresse \(f(n)\) est bornée asymptotiquement et supérieurement par la fonction \(g(n)\). Il existe toujours une valeur \(c\) et une \(n_{0}\) à partir de laquelle \(g(n)\) sera toujours plus grande que \(f(n)\).

Plus que ça, les plus assidus auront remarqué l’usage des accolades \(\{\}\) synonyme d’ensemble. En effet, cette notation reprend ce qui a été dit plus tôt, puisqu’on ne s’intéresse qu’aux termes de plus haut degré, il reste une certaine flexibilité pour le restant des termes, cela décrit donc une très grande famille de fonctions. Inversement, c’est la raison pour laquelle on préfère noter \(O(.)\) lorsqu’on aborde cette notion pour bien insister sur le fait qu’on s’intéresse à des fonctions. \(O(n)\) a donc une sémantique en elle-même, c’est l’ensemble des fonctions bornées par la fonction \(f(n) = cn\).

• Le pendant du “Grand O” est le “Grand Omega” \(\Omega(.)\):

$$\Omega(g(n)) = \{ f(n) | \exists c > 0, \exists n_{0}, \forall n \geq n_{0}, \quad 0 \leq c g(n) \leq f(n) \}$$

Au lieu de chercher une “borne supérieure”, on s’intéresse ici à une “borne inférieure asymptotiquement”, c’est à dire que la complexité de la fonction ne sera jamais inférieure à une autre (à partir d’un certain \(n_{0}\) bien entendu).

• Si on associe les deux notions, on obtient la notion de “(Grand)-Theta” \(\Theta(.)\):

$$\Theta(g(n)) = \{ f(n) | \exists c_{1}, c_{2} > 0, \exists n_{0}, \forall n \geq n_{0}, \quad 0 \leq c_{1} g(n) \leq f(n) \leq c_{2} g(n) \}$$

La fonction \(f(n)\) est bornée supérieurement et inférieurement par les fonctions \(c_{1}g(n)\) et \(c_{2}g(n)\). C’est une relation très forte parce qu’elle borne la fonction \(f(n)\) à une constante près. Cela est équivalent à dire qu’on a à la fois: \(O(g(n))\) et \(\Omega(g(n))\).

Il existe d’autres notations, mais qui ont tendance à être moins utilisées ou tout du moins, confinées à des usages plus spécifiques. Notamment \(f(n) = o(g(n))\) (et \(\omega(.)\)) qui représente le fait que \(f(n)\) est dominé (respectivement, domine) asymptotiquement \(g(n)\). Ainsi que “Soft-O”, noté \(Õ(.)\), qui est défini comme suit: \(f(n) = O(g(n) log^{k}(g(n))) \exists k\) qui traduit l’idée qu’on s’en fiche de certains détails techniques par rapport à l’algorithme en lui-même et que c’est bien la taille des données en entrée (\(n\)) qui incombe. Mais ces notations sont nettement plus marginales et interviennent dans des questions plus avancées.

Analyse de complexité

Une fois que les concepts sont définis, on peut commencer à s’amuser et s’intéresser à différentes problématiques.

La première étape serait de chercher un algorithme, que ce soit en posant un nouveau problème ou en répondant à une question déjà existante. Seulement tous les problèmes ne sont pas forcément intéressants, on cherche, par exemple : des algorithmes représentatifs d’une famille de tâches (trouver un élément dans une collection par exemple), ayant des relations avec d’autres domaines des Sciences (sur des graphes, sur de la logique, sur des systèmes d’équations, …) ou dont la résolution fait preuve d’innovation (un nouvel outil, poser le problème autrement ou un résultat contre-intuitif).

Une fois qu’on a découvert un algorithme, on peut l’analyser pour exprimer sa complexité. Que ce soit pour obtenir une expression précise (afin de mieux évaluer des algorithmes analogues) ou par rapport à différents modèles de calcul (on peut s’intéresser à un aspect temporel sur le nombre d’étapes que prend l’algorithme ou à l’aspect spatial en considérant l’espace mémoire nécessaire pour y répondre). Encore faut-il être capable de pouvoir calculer la complexité du problème, cela peut s’avérer très compliqué, la conjecture de Collatz (ouverte depuis presque un siècle) est un bel exemple.

Une fois qu’on possède un algorithme dont on connaît la complexité, est-ce qu’on est capable d’être plus efficace, de mieux employer les ressources ? C’est la question associée au \(O(.)\). Par essence, si un algorithme est en \(O(n)\), il est également en \(O(n^{2})\), \(O(n^{3})\), … On cherche la fonction la “plus simple” et la “plus petite” qui borne supérieurement l’algorithme ; la définition de “plus simple” est très arbitraire, c’est le même problème que pour définir des fractions “simples”, on cherche une fonction exprimée en un nombre minimal de fonctions élémentaires, généralement : les polynômes, le logarithme ou l’exponentielle. Il se fait que les outils mathématiques ont tendance à exprimer les complexités en faisant intervenir ces fonctions-là, il est exceptionnel de voir apparaître d’autres types de fonctions (celles trigonométriques par exemple).

Mais jusque où on peut aller en efficacité, est-ce qu’on peut toujours faire mieux ? Quelle est la complexité inhérente à un problème, on se dit bien que trier une collection est plus compliqué que de chercher un élément et qu’il ne sera jamais possible que les deux soient aussi simples. C’est la question associée au \(\Omega(.)\). On retrouve les mêmes contraintes que pour la question précédente, sauf qu’on cherche la “plus simple” et la “plus grande” qui borne inférieurement l’algorithme. On définit alors la complexité d’un problème comme étant la meilleure complexité associée à un algorithme qui le résout. Cette question est d’autant plus critique lorsque l’on s’intéresse à la notion de “classe de complexité” qui regroupe les problèmes ayant une complexité minimale équivalente.

Tri

Nous allons illustrer ces notions par un exemple très classique : le tri. C’est une primitive essentielle à une multitude d’algorithmes et c’est un problème relativement simple.

Le problème posé est le suivant : On possède une collection \(L\) de \(N\) éléments et on souhaiterait que tous les éléments soient triés en ne sachant comparer que des éléments deux à deux. Au final, on souhaiterait avoir : \(\forall i, \forall j > i, L[i] < L[j]\) en notant \(L[i]\) l’élément à la \(i\)e position dans la collection.

On va chercher à étudier deux solutions à ce problème en analysant la complexité liée à deux algorithmes choisis. On présentera les idées de la démonstration des complexités associées à ces algorithmes et on finira par donner des indications sur la complexité minimale de ce problème en particulier.

Tri par sélection :

Une solution simple au problème est le tri par sélection, il consiste à toujours sélectionner le plus petit élément et à le rajouter à la liste déjà triée.

def tri_par_selection(L): N = len(L) # On cherche à chaque fois l'élément le plus petit dans tous ceux qui restent, toutes les positions plus petites que i sont triées. for i in range(N): # On cherche l'élément le plus petit situé après la position i min_idx = i for j in range(i + 1, N): if L[min_idx] > L[j]: min_idx = j   # On échange le plus petit élément qu'on a trouvé avec la valeur à la position i L[i], L[min_idx] = L[min_idx], L[i]

Lorsqu’on commence l’algorithme, il faut chercher le plus petit élément parmi tous les éléments \(N\), puis dans \(N-1\) parce qu’on sait que tous les éléments restants sont supérieurs au premier élément commençant à former la liste triée, puis \(N - 2\) parce qu’on connaît les deux premiers éléments, et ainsi de suite … et ce, jusqu’à 0. On effectue bien cela \(N\) fois, ce qui correspond à la première boucle for.

On effectuera donc : \(N-1 + N-2 + ... + 1 = \sum_{i=0}^{N-1}i = \frac{1}{2}N(N-1)\) comparaisons au total et \(N\) échanges de positions, car on commence par considérer le premier élément comme base de comparaison, donc c’est bien \(N-1\).

La complexité s’exprime donc de la forme : $$f(N) = \frac{1}{2}N(N - 1) + N = \frac{1}{2}N(N + 1) = \frac{N^{2}}{2} + \frac{N}{2} = O(N^{2})$$

Tri fusion :

Le tri fusion consiste à fusionner de plus petites listes triées ensemble afin d’arriver à une plus grande liste triée, et ce, récursivement jusqu’à arriver à la solution. Le principe de base étant que, par définition, un élément esseulé est trié. On commence donc par diviser récursivement la liste en plus petites listes jusqu’à arriver à des éléments uniques. On commence alors à les fusionner, ce qui est relativement simple à faire parce que les sous-listes sont déjà triées.

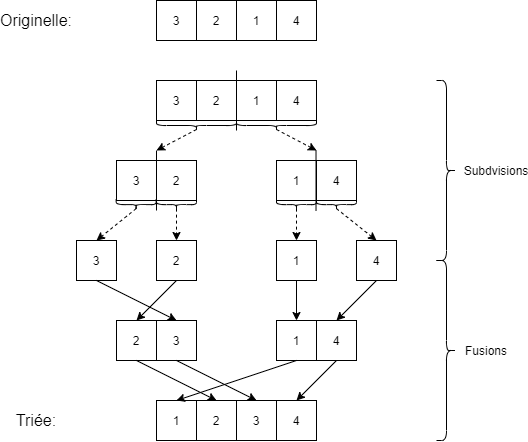
On peut transcrire la logique dans un langage de programmation tel que Python :

def tri_fusion(L): tri_fusion_recursif(L, 0, len(L))   def tri_fusion_recursif(L, p, r): # On trie les données dans l'interval qui va de p à r if p < r: # On prend l'élément situé au milieu de l'interval p et r q = floor((p + r) / 2) # On effectue la même procédure sur la partie gauche tri_fusion_recursif(L, p, q) # Ainsi que la droite tri_fusion_recursif(L, q, r) # On fusionne les deux parties fusion(L, p, q, r)   def fusion(L, p, q, r): # On fusionne les deux sous-listes entre p et q, et q et r p_i = p q_j = q liste_triee = [] while p_i < q and q_j < r: # Si l'élément dans la première liste est plus petit que dans la seconde if L[p_i] < L[q_j]: # On l'ajoute et on passe à l'élément suivant dans la première liste liste_triee.append(L[p_i]) p_i += 1 else: # Sinon, on rajoute l'autre élément à la liste liste_triee.append(L[q_j]) q_j += 1   # On quitte la boucle while parce qu'on a parcouru tous les éléments d'une des deux listes alors qu'il peut rester encore des éléments à trier, il faut donc rajouter ceux qui manquent. liste_triee.extend(L[p_i:q]) liste_triee.extend(L[q_j:r]) L[p:r] = liste_triee[:]

La complexité d’un tel algorithme est déjà plus compliquée à évaluer. Commençons par nous intéresser à la fonction de fusion. On “sait” qu’on ne considère qu’une seule fois chaque élément des deux sous-listes. On peut avoir deux situations extrêmes :

• Soit les listes sont inter-mêlées, le premier élément de la première liste (\(L_{1}\)) est plus petit que le premier de la seconde (\(L_{2}\)), mais le premier élément de \(L_{2}\) est plus petit que le second de \(L_{1}\) et ainsi de suite. Il est assez clair qu’on va devoir faire \(L_{1} + L_{2}\) comparaisons parce qu’on va constamment alterner entre les deux listes.

• Soit les listes sont parfaitement disjointes, tous les éléments de la seconde liste sont plus grands que ceux de la première. Dans ce cas, on va épuiser la première liste entièrement et puis rajouter la seconde liste à la suite, on n’aura effectué que \(L_{1}\) comparaisons.

La complexité de la fusion est bornée par \(O(L_{1} + L_{2})\).

Quant à la fonction tri_fusion_recursif, on subdivise à chaque fois les listes en deux parts égales (jusqu’à arriver à des éléments uniques), la longueur de \(L_{1}\) est donc la même que \(L_{2}\) (à une considération près, parce qu’on a rarement \(N\) qui est pile une puissance de 2). Il n’est possible de subdiviser \(N\) éléments, en 2, que “\(\log_{2} N\) fois”.

Maintenant observons que, la première étape consiste à fusionner les éléments esseulés, on doit donc appliquer \(\frac{N}{2}\) fois la fusion de liste de longueur \(1\), on a donc \(\frac{N}{2} * (1 + 1) = N\) pour la première étape, puis on va fusionner des listes de longueurs \(2\), mais on n’en aura que \(\frac{N}{4}\), on obtient donc \(\frac{N}{4} * (2 + 2) = N\). A chaque étape de l’algorithme, la quantité de travail à effectuer est à la même (ici \(N\)) et il n’y a \(\log_{2} N\) étapes possibles au maximum.

La complexité est donc bornée par : \(O(N \log N)\). Observer qu’on note généralement \(\log\) sans spécifier la base suite à la formule du changement de base des logarithmes qui ne multiplie que par une constante. Ce \(O(N \log N)\) est très largement meilleur que le tri par insertion en \(O(N^{2})\), si on prend \(N = 1'000'000\), on aurait \(1, 37 * 10^{7}\) opérations au lieu de \(10^{12}\).

Master Theorem :

L’argument que nous avons employé pour calculer la complexité du tri fusion est lié à un théorème qu’on appelle “Master Theorem” ¹. Il s’agit d’un théorème mathématique qui visait à unifier toute une famille de démonstrations sur la complexité des algorithmes où on a la propriété qu’on effectue le même travail (ici la fusion), à chaque étape de l’algorithme. C’est un théorème plus profond parce qu’il permet de “résoudre” des systèmes d’équations fonctionnelles qui sont récurrentes (qui font appel à elles-mêmes) mais qui doit être appliqué dans des conditions très précises.

Cela permet de répondre à trois types de cas :

• Soit on a de plus en plus de sous-cas dont la somme des complexités des nœuds terminaux dépasse toute la complexité introduite par les étapes précédentes (complexité croissante).
• Soit la charge de travail reste constante en fonction des étapes (complexité constante) et il ne reste plus qu’à multiplier la complexité d’une étape par la hauteur de cet arbre de complexité. Le cas que nous avons rencontré avec le tri fusion.
• Soit la charge de travail diminue parce qu’on est capable d’évincer des pans entiers dans les données (complexité décroissante).

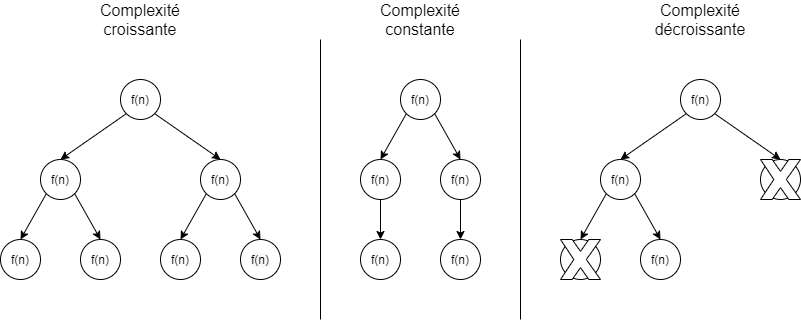
Ce n’est pas le seul type de démonstration pour les études de complexité des algorithmes, mais cela englobe une bonne partie des problèmes usuels.

Complexité minimale :

Nous l’avons vu, un algorithme naïf de tri est en \(O(N^{2})\), en réfléchissant beaucoup, on voit qu’on peut arriver en \(O(N \log N)\). Mais est-il possible de faire mieux ?

La réponse est comme souvent : “ça dépend”. Au sens commun, il est largement accepté que \(\Omega(N \log N)\) est la complexité minimale pour trier une liste si on ne possède que l’opérateur de comparaison deux à deux. On peut pinailler sur le fait que : 1) si l’on change de modèle de calcul, la réponse peut très largement variée et même devenir en \(\Omega(N)\) si on ne travaille qu’avec des entiers. 2) on peut obtenir des bornes un peu plus précises, mais qui restent néanmoins bornée sémantiquement par \(\Omega(N \log N)\).

Une démonstration particulièrement élégante de cette complexité minimale est issue d’un modèle de calcul basé sur des arbres algébriques (algebraic computation trees) ², qui correspondent, sans rentrer dans les détails, à la limite qu’on s’impose : “On ne peut considérer que deux éléments à la fois et dire si l’un est plus petit que l’autre”. L’argument est le suivant :

À chaque étape de l’algorithme, on n’est capable que de comparer deux éléments. Quelle que soit la réponse de cette comparaison, il faudra effectuer un choix. On aura donc deux embranchements possibles, qui vont aboutir eux-mêmes à répondre à une nouvelle question sur la comparaison de deux éléments, éventuellement nouveaux. Or, on sait que toutes les permutations de la liste initiale sont possibles (\(N!\)). Et on veut que notre algorithme donne la réponse correcte pour tous ces cas, il doit donc être possible, à partir de n’importe quelle réponse d’une comparaison, d’arriver à cette liste triée. Et à chaque fois, on a deux possibilités, soit la comparaison disait que \(a\) était inférieur à \(b\), soit l’inverse. Le nombre de chemins possibles croît de manière exponentielle \(2^{k}\). Il ne reste plus qu’à égaler les deux, on aura notre réponse :

$$2^{k} \geq N! \Leftrightarrow k \leq \log_{2}(N!) \approx k = \Omega(N \log N)$$

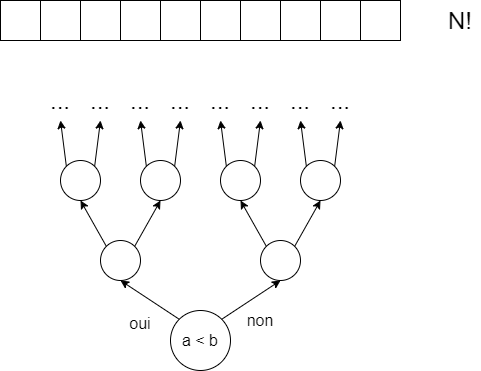
Pour l’équivalence du \(\log_{2}(N!)\), il faut invoquer des notions plus avancées, mais faisons remarquer que \(N! = \prod_{i=1}^{N}i\) et que le logarithme d’un produit est la somme des logarithmes et donc qu’on a \(\sum_{i=1}^{N}\log i \geq \frac{N}{2}\log{\frac{N}{2}}\), ce qui est bien borné par \(O(N \log N)\). On peut également invoquer la formule de Stirling ou les travaux de Landau (à qui on attribue l’invention du symbole \(o(.)\)) pour fournir des bornes plus “précises”. Il s’agit ici d’une démonstration dite universelle, on montre que toutes les instances du problème, toutes les configurations initiales possibles, tous les cas, peuvent s’exprimer au travers de cet argument, mais il existe des existentielle, où on démontre qu’il existe au moins un cas, une instance, où il est nécessaire d’atteindre cette complexité.

Aller plus loin

Dans cet article, nous n’avons fait que survoler des concepts de base liés à la notion de complexité et avons montré, sur un cas concret, les différents aspects qui pouvaient intervenir. Tout ceci n’était qu’une petite introduction par rapport à la multitude de questions qu’on peut se poser en s’intéressant davantage à la nature des choses.

Nous avons abordé, ici, la notion de complexité, mais celle-ci englobe d’autres sous-catégories. Que ce soit en fonction de la situation initiale en entrée, on peut s’intéresser au cas moyen (une distribution aléatoire en entrée), au meilleur (celui qui nécessite le moins d’étapes) ou au pire cas (celui qui en nécessite le plus). Si la liste est déjà triée, il y aura sans doute moins de travail à effectuer que dans une configuration aléatoire ou très particulière par rapport à l’algorithme (imaginons qu’elle soit triée dans le sens opposé). Comment faut-il alors définir le cas moyen ? Peut-on toujours déterminer les motifs liés au pire ou meilleur cas ?

Il existe également une question opposée, quels sont tous les algorithmes qui ont pour complexité \(\Omega(N \log N)\) ? Quid des autres, pourquoi ces différences ? Des tentatives de réponses sont données par la définition de classes de complexité, ensemble de problèmes dont la complexité est “équivalente”. Ce sont des questions particulièrement ardues, qui nécessitent une grande rigueur dans leur définition ; les classes sont toutefois définies en termes de \(O(.)\), même si l’on cherche la plus petite classe englobante d’un problème. La raison ontologique des différences de complexité est rarement connue et on est, parfois, capable d’expliquer que des familles de problèmes ne pourront jamais avoir la même complexité que d’autres, mais de nombreux problèmes sont ouverts dans ce domaine depuis plus d’un cinquantenaire …

Les modèles de calcul sont fort abstraits et associent une complexité unitaire à des opérations qui sont pourtant intuitivement différentes, additionner deux nombres semble plus simple que les diviser.

• On peut alors chercher à avoir des modèles de calcul plus précis, qui s’intéressent à la complexité intrinsèque de ces opérations de bases en étudiant la complexité par rapport au nombre de bits ou le nombre de portes logiques nécessaires ¹ ; cela a d’ailleurs donné naissance à des algorithmes de tri basé sur des réseaux, où on construit un circuit fixe dans lequel les données vont passer et ressortir magiquement triées ².
• L’ordinateur sur lequel on va exécuter l’algorithme aura peut-être plus de faciliter avec certaines opérations par rapport à d’autres, et il sera parfois préférable d’employer des algorithmes ayant des complexités asymptotiques plus élevées, mais qui possèdent de meilleures performances pour les tailles de données qui nous intéresse parce que les facteurs multiplications d’un algorithme “théoriquement” meilleur le rendent en réalité moins intéressant.
• Plus fort encore, on peut démontrer que certaines propriétés sont dites oblivious, c’est-à-dire que cet algorithme est optimal peu importe les conditions dans lesquelles il est appliqué. On sait qu’il ne sera pas possible de faire mieux en terme de complexité pour la propriété qui nous intéresse dans le cadre général. C’est un saint Graal en informatique qui a déjà été atteint de nombreuses fois.

Nous avons laissé envisager que la complexité d’un problème était lié à la taille en entrée. Mais ce n’est qu’une vision partielle, il existe des problèmes dont la complexité peut dépendre de la taille du résultat en sortie. Par exemple : si je divise deux nombres (en les soustrayant), plus le résultat est petit, moins j’ai dû faire de soustractions. Ou encore, il existe des algorithmes qui dépendent à la fois de l’entrée et de la sortie ³.

À l’heure actuelle, il est de plus en plus rare de considérer un algorithme sans ses possibilités de parallélisme, donc d’avoir plusieurs machines qui collaborent pour produire le résultat d’un problème. Cela entraîne de nouveaux problèmes théoriques pour savoir s’il est possible d’avoir des algorithmes équivalents à ceux séquentiels alors qu’il faut faire communiquer de l’information entre ces machines. Parcourir un graphe en parallèle est quelque peu plus ardu qu’en séquentiel. Quelles sont les conséquences du parallélisme sur la quantité d’information à échanger ou l’espace additionnel en mémoire qu’il faut alors gérer. On a également vu apparaître plus récemment des problématiques liées au réseau et à sa communication où il faut faire intervenir le nombre de machines qui discutent ainsi que le temps mis pour transférer l’information entre-elles ⁴.

Nous n’avons également pas fait part de la possibilité d’employer de l’aléatoire dans notre algorithme. Cela peut paraître surprenant, mais il est parfois intéressant de proposer une solution aléatoire et d’arriver petit à petit à une solution correcte, ou de baser les décisions sur le résultat d’un processus stochastique (Las Vegas algorithm ⁵), on parle d’algorithme aléatoire (randomized). Encore plus étonnant, on peut consentir à avoir une marge d’erreur dans les résultats parce que cette complexité, qui dépend du nombre d’erreurs qu’on tolère, peut être largement plus intéressante qu’un algorithme exact, on les qualifie de probabiliste (probabilistic).

En algorithmique, l’autre point capital à tout programme est l’usage des structures de données (Algorithms + Data Structures = Programs comme disait Wirth ⁶). Il y aurait une quantité astronomique de choses à dire sur celles-ci tant elles peuvent être liée intimement à certains algorithmes. Au-delà de ça, on peut se demander quelles sont les complexités de certaines opérations (pour insérer un élément, pour trouver son prédécesseur, …), ces questions sont complexes parce qu’il s’agit d’un doux mélange entre la complexité attendue par chaque opération et le nombre d’opérations qu’il est possible d’effectuer sur celles-ci. On peut se permettre d’éventuellement de ne jamais devoir supprimer un élément, mais il faut que la recherche du prédécesseur soit absolument en \(O(1)\) par exemple. C’est généralement la contrainte de certaines opérations plus rapides au regard d’autres qui fait émerger ces nouvelles structures de données.

Un concept qui est intimement lié à ces structures de données est la complexité par rapport à non pas une seule opération, mais par rapport à une suite d’opérations (ce qui est plus représentatif de l’usage qu’on en fait en pratique). Cela peut se transcrire par des concepts de stratégie sur les opérations internes à la structure de données, si on attend d’avoir un nombre suffisant d’insertions ou de suppressions avant d’effectuer les changements adéquats par exemple. Cela a abouti à la notion en complexité dite OPT, parfois notée \(O_{OPT}\), définie comme suit: étant donnée une séquence d’opérations connues à l’avance - qualifiée d’offline (ou non, inconnues, - dite online) et généralement notée \(\sigma\), il s’agit de la complexité optimale qui pourrait être atteinte sous ces conditions. C’est un concept théorique qui représente la plus petite complexité possible qui respecte la suite d’opérations. Il s’agit d’un concept extrêmement fort en algorithmique et dont certains résultats sont connus comme étant à un facteur multiplicatif près, on qualifie parfois cette complexité de competitive si \(ALG(\sigma) \leq c * OPT(\sigma)\). Cet aspect compétitif s’intéresse à la comparaison de complexité entre le cas online et le meilleur algorithme offline possible.

On a parlé de mesurer le nombre d’opérations nécessaires pour arriver à une solution ou du réseau. Mais on ne s’est pas intéressé à l’espace mémoire nécessaire pour répondre à la question et ses éventuels liens avec la complexité temporelle que cela peut entraîner. Un autre modèle de calcul, apparu plus récemment, s’intéresse au dénombrement des transferts de données entre une mémoire infinie et une plus petite mémoire, l’idée étant qu’accéder à une donnée située à l’autre bout de l’internet est plus lent que de faire une simple addition. À l’air du réchauffement climatique, des modèles ont également été développés afin d’étudier l’énergie dépensée par des algorithmes, ce qui possède plusieurs applications dans le domaine de la sécurité. Il y a également toutes des panoplies liées à des machines spéciales, basées sur des formules mathématiques, sur des modèles d’ordinateur quantique, sur des machines plus puissantes que celle de Turing, …

Conclusions

On espère que ce tour rapide de l’algorithmique et des problèmes liés à la complexité vous aura intéressé suffisamment pour essayer d’aller voir plus loin, qu’on aura su titiller votre esprit et que vous vous poserez plein de nouvelles questions. Je ne peux que vous conseiller le livre de Cormen, Leiserson, Rivest et Stein: Introduction to algorithms ¹ qui est une introduction assez complète de l’algorithme et qui aborde une quantité astronomique d’algorithmes classiques par catégorie (graphes, structures de données, …) et par type (séquentiel, probabiliste, …), des preuves de complexité ainsi que des fondements mathématiques associés aux résultats. Il est aussi souvent conseillé un livre un peu plus ancien de Hopcroft, Motwani et Ullman: Introduction to automata theory, languages, and computation ² qui s’oriente davantage vers les origines de l’algorithmique.

Pour des fondements mathématiques, le livre Computation Complexity de Papadimitriou ³ est un classique et contient des démonstrations rigoureuses des classes de complexité notamment. Une version plus moderne est proposée par Arora et Barak dans Computation complexity: a modern approach ⁴. Enfin, comment parler d’algorithmique sans parler de la bible de Knuth: “The art of computer programming” ⁵, véritable travail d’une vie et ontologie de l’informatique, mais qui s’intéresse malheureusement uniquement à un petit nombre de problèmes, mais de manière très exhaustive.