Introduction

Dans cette (brève) introduction à l'I/O complexité, nous allons étudier des algorithmes dans un modèle de calcul différent. Souvent, durant les études, un modèle temporel de type RAM est employé afin de déterminer la complexité d'un algorithme. Il est en effet très naturel et propose une analyse proche de la conception mentale du problème. Seulement, il ne laisse pas transparaître certains phénomènes.

Dans cet article, nous retracerons rapidement les idées qui ont permis l'émergence de cette famille de modèles de calcul qui se consacre non pas à l'analyse temporelle des algorithmes (leur nombre d'opérations) mais bel et bien au nombre d'accès nécessaires afin de résoudre le dit problème et qualifiés d'I/O puisqu'on quantifie le nombre d'entrées/sorties des données. Nous commencerons par revenir brièvement sur des modèles qui ont présenté des tournants majeurs dans ce domaine par le biais d'un bref historique. Nous nous concentrerons alors sur un modèle bien précis : External Memory (souvent abbrévié « EM ») et verrons différents résultats obtenus dans celui-ci, avec quelques démonstrations. Enfin, nous terminerons sur une variante de ce modèle qui présente un aspect fort novateur et puissant : la notion d'« obliviousness ».

Ce texte requiert certaines bases en algorithmique, mais reste relativement abordable pour des étudiants du supérieur (master ou bachelier enthousiaste). Connaître a priori les notions de complexité classiques (notation grand O) est une condition nécessaire ainsi que le fonctionnement de certains algorithmes classiques. La connaissance du Master Theorem et des bases en théorie de l'information est un plus non négligeable.

Contexte

Les notions liées à l'I/O complexité sont apparues au début des années 70 mais n'ont vraiment été popularisées que vers la fin des années 80 avec l'apanage qu'on leur a connu lors de la charnière année 2000 et l'implémentation de certains résultats dans le cadre des bases de données. Elles sont issues de différents phénomènes qui ont émergé petit à petit et pour des raisons fort spécifiques.

Modèle de calcul

Avant de nous étendre sur le sujet. Il serait peut-être intéressant de revenir sur un point, la définition d'un modèle de calcul. Un modèle de calcul est avant tout un concept, une représentation d'une machine physique ou abstraite, qui décrit comment des sorties sont calculées sur la base d'entrées. Ce modèle peut être plus ou moins précis et définit quelles sont les unités de calcul (quelles sont les opérations de base, quel coût est requis pour additionner deux nombres ou pour accéder à un élément, par exemple) ainsi que de la manière dont est structurée la mémoire ou les communications. La complexité d'un algorithme est donc intimement liée à un modèle de calcul. Ceux-ci permettent d'étudier des algorithmes indépendamment de leur implémentation et offrent donc une manière de les comparer.

À la recherche du temps perdu

Classiquement, lorsqu'on apprend aux étudiants les notions de complexité, on le fait au travers d'un modèle de calcul spécifique et temporel. Ce modèle de calcul qualifié de « (word-)RAM » n'est pourtant apparu qu'en 1990¹ ! Il est conceptuellement très simple et correspond fort bien à la perception que l'on se fait de la complexité (en simplifiant, c'est le modèle qui se rapproche des capacités du C). On associe à chaque opération un coût unitaire \(O(1)\), que ce soit une addition, une multiplication, un accès mémoire, un saut dans un branchement conditionnel,... Et les complexités supérieures apparaissent naturellement, comme lorsqu'on doit parcourir une collection de \(N\) éléments avec son facteur \(O(N)\) associé, par exemple. Rien de bien sorcier.

Seulement, celui-ci présente certains défauts :

• Premièrement, toutes les opérations de base sont en temps constant. Or, on comprend bien que l'évaluation d'une fonction « sinus » prend plus de temps qu'effectuer un « and » entre deux nombres. On présente généralement un aspect haut niveau pour ces opérations, et on revient plus précisément sur ces notions uniquement si l'on doit calculer la complexité de manière plus précise afin de déterminer quel algorithme choisir pour évaluer la fonction sinus de la manière la plus rapide possible. On se tourne alors davantage vers des aspects plus quantitatifs que qualitatifs et on abandonne les modèles de calcul pour se baser uniquement sur des benchmarks.
• Deuxièmement, il ne permet pas de représenter des phénomènes plus complexes liés à des accélérations matérielles. Par exemple, une opération peut prendre plus ou moins de temps en fonction du contexte. Nous évoquons notamment le cas des « branch prediction » ou des instructions SIMD.
• Troisièmement, qu'en est-il de la complexité liée à la mémoire ? Écrire dans un fichier est-il réellement en \(O(1)\) ? Vaut-il mieux accéder à tous les éléments de manière contiguë et non de manière aléatoire ? Ce sont sans doute les points les plus discutables de ce modèle.

Il faut comprendre que bien d'autres modèles de calcul ont été proposés en vue de résoudre spécifiquement ces problèmes ou, plus généralement, proposer de nouvelles approches, techniques et outils aux chercheurs. Il existe plusieurs familles de modèles de calcul, liés à des machines (thèse de Turing), à des aspects fonctionnels (thèse de Church), à de la concurrence (par exemple les réseaux de Pétri) ou à des concepts plus abstraits (par exemple le modèle de l'Oracle). Et ceux-ci peuvent présenter différents aspects sur lesquels on peut se pencher indépendamment telle que la dualité temps-espace de la machine de Turing, par exemple. Ceux travaillant dans les milieux distribués et ayant attrait au Big Data penseront à des modèles plus spécifiques comme BSP ou MapReduce.

Les débuts de l'I/O complexité - Floyd

Le temps d'accès aux ressources est certes un des principaux défauts du modèle RAM (et de ces prédécesseurs), mais ce n'est pas ce qui a motivé l'apparition de l'I/O complexité. En 1972, Robert W. Floyd² (prix Turing 1978, auteurs de très nombreux travaux et entré à l'université à l'âge de 14 ans), introduit un modèle de calcul un peu particulier en vue de répondre à une problématique bien précise. Les mémoires de l'époque étaient extrêmement petites, quelques KB, et les disques durs à peine plus, de l'ordre du MB, mais souvent bien moins. Il était donc impossible de faire tenir toutes les données directement en mémoire et il s'était demandé combien de transferts étaient nécessaires afin de permuter l'ensemble des éléments d'un même « fichier ». On cherche donc à comptabiliser le nombre de transferts mémoire effectués et qui correspondent à chaque fois à une entrée ou une sortie, une I/O.

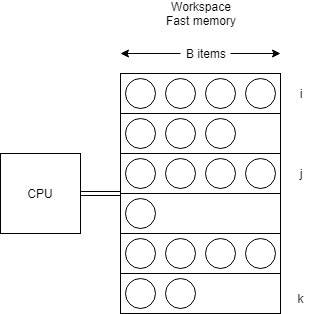
Ce modèle d'ordinateur se décrit comme suit :

• La RAM est composée de blocs d'au maximum \(B\) objets.
• On est capable de lire jusqu'à \(B\) objets provenant de deux blocs (\(i, j\)) en même temps et d'écrire dans un troisième (\(k\)). Ceci détermine l'opération en \(O(1)\) de ce modèle.
• L'ordre des éléments dans un bloc n'a aucune importance.
• Les opérations effectuées sur le CPU n'ont pas de coût.
• Les objets sont atomiques, on ne peut pas les diviser en plusieurs objets.

Vous en conviendrez, ce modèle est très spécial. Il a néanmoins permis d'établir un théorème :

Permuter N éléments dans \(\frac{N}{B}\) blocs (préalablement définis et remplis) nécessite \(\Omega(\frac{N}{B} \log B)\) opérations en moyenne. Sous l'hypothèse que \(\frac{N}{B} > B\).

Pour trouver cette complexité, il définit une fonction dite de « potentielle ». Cet outil sera employé de très nombreuse fois par la suite afin de démontrer des propriétés dynamiques sur des structures de données. Elle est définie comme suit : \(\Phi = \sum_{i, j} n_{i, j} \log n_{i, j}\) où la quantité \(n_{i, j}\) représente le nombre d'objets du bloc \(i\) destiné au bloc \(j\).

Certains verront des similitudes avec les travaux de Shannon, notamment, portant sur l'entropie et la théorie de l'information. L'argument s'exprime comme suit : nous cherchons à maximiser ce potentiel (puisque c'est l'« inverse » de l'entropie), plus nous sommes loin de la configuration visée, plus nous devrons effectuer d'opérations. Et inversement, si tous les objets sont déjà à leur place (\(n_{i,i}\) pour chaque \(B\)), on obtient \(\Phi = N \log B\).

Au début, dans une configuration aléatoire, l'entropie est faible. L'espérance pour chaque élément d'être à sa position finale est faible : \(E[n_{i,j}] = O(1)\) (à condition qu'il y ait plus d'éléments que de blocs), le potentiel a donc une espérance linéaire : \(E[\Phi] = O(N) \approx N * O(1)\). Les opérations visent donc à augmenter le potentiel afin d'arriver à ce facteur \(\log B\) de différence. Or, chaque opération ne peut augmenter ce potentiel qu'au maximum de \(B\). Il faut voir cela au travers du fait que fusionner deux blocs n'entraîne qu'une augmentation en termes de leurs nombres (\((x + y) \log (x + y) \leq x \log x + y \log y + x + y\)). Le nombre d'opérations est donc déterminé comme suit:

$$ \text{Nombres d'opérations} \geq \frac{N \log B - O(N)}{B} $$

Red-blue pebble game de Hong & Kung

Vous en conviendrez, le modèle précédent, de Floyd, tombe un peu comme un cheveu sur la soupe. Il est difficile de voir son intérêt réel. Néanmoins, son article initiateur lançait quelques pistes de réflexions et des problématiques qui ont mené à cette branche de l'algorithmique. Il y a eu quelques variantes par rapport au modèle de Floyd³, mais rien de transcendant.

La prochaine grande innovation dans cette branche fut le modèle développé par Hong Jia-Wei et Hsiang-Tsung Kung en 1981⁴ et appelé (érronément) Hong & Kung. Ils ont démontré la complexité de différents algorithmes grâce à un jeu , le « Red-blue pebble game » (jeu des galets rouges-bleus, littéralement). L'idée est qu'effectuer des transferts mémoires est long (surtout à l'époque des bandes magnétiques où c'était parfois manuel) et on cherche donc à minimiser de telles opérations. Ils partent sur une toute autre vision du problème (sur base de travaux effectués quelques années auparavant et établissant un lien entre la complexité temporelle et spatiale⁵).

On associe à un algorithme un graphe de calcul. Celui-ci s'exprime au travers d'un graphe dirigé acyclique (DAG) où chaque nœud \(v\) correspond, soit à une entrée (s'il n'existe pas d'arêtes entrantes), soit à une sortie (s'il n'y a pas d'arêtes sortantes), ou soit à un calcul où les arêtes représentent les dépendances entre les opérandes.

L'idée est de jouer à un jeu, sur ce graphe de calcul, basé sur quelques règles. Un galet rouge représente de la mémoire interne et rapide et bleu externe et lente. On peut mettre un galet bleu sur un rouge ou vice-versa, cela représente un transfert de données entre les deux types de mémoire. La complexité s'exprime donc en terme du nombre de transferts effectués entre deux endroits. De surcroît, nous avons besoin d'avoir toutes les arêtes entrantes couvertes de galets rouges afin d'effectuer un calcul et de faire naître un nouveau galet rouge. Nous pouvons également enlever les galets à tout moment et nous pouvons disposer d'au maximum \(M\) galets rouges en même temps sur le graphe. Le but du jeu consiste à couvrir certains nœuds de sortie avec des cailloux bleus selon une distribution bleue initiale.

Ils ont prouvé qu'un partitionnement du graphe de calcul donnait une limite inférieure sur le nombre d'opérations d'I/O. Tout ensemble de partitions peut avoir un ensemble dominant (nœuds à partir desquels il existe un chemin des nœuds d'entrée vers cet ensemble, le flux d'exécution) d'une taille maximale de \(2M\). Et qu'il en existe au maximum \(\mathcal{P}(2M)\) (avec \(\mathcal{P}(.)\) l'ensemble des parties d'un ensemble) et donc que le nombre minimal d'I/O est borné par \(M (\mathcal{P}(2M) - 1)\). On peut exprimer la complexité par rapport à ce \(M\) par la fonction W de Lambert.

Ils ont alors démontré la complexité de nombreux problèmes qui pouvaient s'exprimer sous la forme d'un DAG (certaines conjectures impliquent une correspondance par rapport à certains problèmes polynomiaux ou avec la classe de complexité \(AC^{0}\)). Notamment, que calculer une transformée de Fourier était en \(\Theta(N \log_{M} N)\) (ce qui peut être vu comme une forme particulière de permutations), la multiplication d'un vecteur et d'une matrice en \(\Theta(\frac{N^{2}}{M})\), la multiplication de deux matrices en \(\Theta(\frac{N^{3}}{\sqrt{M}})\), et ainsi de suite...

Travaux postérieurs

Quelques modèles dérivés ont fait leur apparition dans les années qui ont suivi. La principale innovation consiste en la représentation de différents niveaux de mémoire avec leur propre caractéristique en termes de vitesse. Ceci vise à représenter les ordinateurs actuels, composées d'une hiérarchie de mémoire possédant des caractéristiques diverses, d'une vitesse prodigieuse et faisant quelques KB pour les caches L1 des CPU, à des GB pour une bande passante raisonnable pour les barrettes de mémoire. On parle notamment du modèle HMM⁶ qui vise à représenter une hiérarchie infinie, avec la notion de politique de remplacement dans les caches. Seulement, ils sont généralement moins commodes à employer. On leur préfère généralement une version plus simple dite « EM » avec seulement deux niveaux de mémoires. En outre, ils ont été élégamment généralisés par la notion de cache-obliviousness qui offre des propriétés beaucoup plus fortes et sur laquelle nous reviendrons plus tard.

External Memory

Les deux modèles présentés précédemment sont très différents. D'un part, Floyd introduit la notion de blocs mais sans la notion de cache, et d'autre part, Hong & Kung introduisent le cache (zone où sont effectués les calculs) mais ignorent les blocs.

Heureusement, Alok Aggarwal et Jeffrey S. Vitter introduisent, en 1988¹, le modèle de calcul External Memory (ou anciennement appelé Disk Access Model) qui réunit ces deux aspects en un. La complexité est déterminée par le nombre de transferts de blocs effectués lors de l'algorithme, sous l'hypothèse d'une mise à jour du cache optimale. Toutes les opérations de calcul effectuées en cache sont donc originellement sans coût (ceci implique que, par essence, on possède en tout temps les éléments d'un même bloc triés, voir même l'entièreté du cache trié).

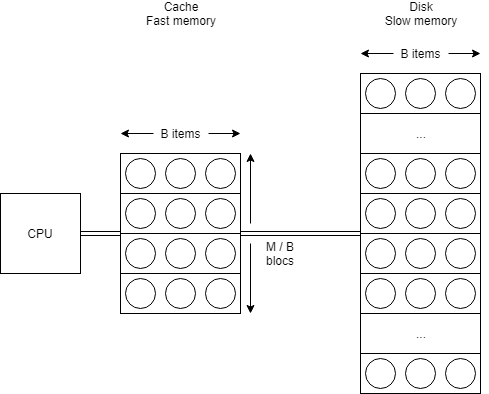
Formellement, il est défini par un ensemble de variables :

• N = la taille du problème (en termes d'objets).
• M = la taille de la mémoire interne (cache) (en termes d'objets).
• B = la taille des blocs transférés (en termes d'objets).
• P = le nombre de blocs transférés simultanément (originellement introduit, mais ne présente un réel intérêt que dans son extension appelé Parallel Disk Model²).

Par la suite, de nombreux résultats feront l'hypothèse que \(M \geq B^{O(1)}\) (ou sous une forme plus faible \(M = \Omega(B^{1 + \epsilon})\)). Cette hypothèse est nommée « tall-cache assumption » puisqu'elle sous-tend qu'il existe plus de blocs dans le cache que la taille de ceux-ci en termes d'éléments. Gerth S. Brodal et Rolf Fagerberg³ ont démontré que, sans cette hypothèse, trier ne peut pas être effectué de manière optimale (et que permuter les éléments n'est pas cache-oblivious même sous cette propriété, mais nous reviendrons sur cette notion plus tard).

L'article en lui-même aborde sur de nombreux aspects, des complexités triviales, des preuves d'optimalité et l'équivalence avec le modèle de Hong et Kung. Nous reviendrons sur certains algorithmes plus en détail. Ici, nous aborderons leur théorème principal :

La complexité pour permuter \(N\) éléments est de: \(\Theta(\text{min} \{N, \frac{N}{B} \log_{\frac{M}{B}} \frac{N}{B} \})\).

Cette complexité peut quelque peu étonner. Elle est d'ailleurs qualifiée de « quasi-linéaire » puisque la base du logarithme gomme presque entièrement le facteur additionnel.

À haut niveau, l'argument peut être exprimé comme suit. Trier les éléments est un cas spécial des permutations. Or, nous pouvons conserver le cache trié sans le moindre coût. Maintenant, si nous effectuons un transfert en mémoire interne, nous pouvons apprendre où se situent ces \(B\) éléments parmi tous les éléments déjà présents dans le cache \(M\). Il faut donc dénombrer toutes les manières possibles de placer ces \(B\) éléments dans le nouvel ensemble formé par la fusion des deux : \(M + B\), soit \(\binom{M + B}{B}\) ou par complémentarité \(\binom{M + B}{M}\). Au final, nous devons connaître la position de chacun des éléments ou réciproquement être capable de générer n'importe quelle configuration originelle. Les éléments n'ayant pas de structure, toutes les permutations de ceux-ci sont possibles, soit \(N!\).

Si nous empruntons un argument issu de la théorie de l'information, nous pouvons prendre le logarithme de chacune des expressions et effectuer le rapport afin de déterminer la quantité minimale de gain d'information nécessaire en vue de résoudre le problème.

$$\log N! = N \log N \text{et} \log \binom{M + B}{M} \approx B \log \frac{M}{B} \rightarrow \frac{N \log N}{B \log \frac{M}{B}} \approx \frac{N}{B} \log_{\frac{M}{B}} \frac{N}{B} $$

Voici la vision rétrospective du problème, mais une preuve différente a été effectuée originellement. L'idée est de borner le nombre maximum de permutations qui peuvent être produites par au plus \(T\) I/Os, nous recherchons donc le pire cas du nombre de transferts requis pour effectuer \(N!\) permutations. Seulement, une fois que nous avons un bloc en mémoire interne, nous pouvons faire toutes les permutations sans coût (un facteur \(B!\)) et nous savons qu'il y a \(N/B\) blocs en tout, ce qui conduit à \(N! / B!^{\frac{N}{B}}\) possibilités de permutations.

Maintenant, nous devons considérer ce qui se passe quand nous considérons une entrée ou une sortie du problème. Chaque fois qu'un nouvel élément est pris en compte, le même processus doit être effectué (cette action doit donc être répétée \(N\) fois). Nous devons aussi nous rappeler qu'une fois que nous avons un bloc, nous pourrons générer toutes ses permutations. Donc, nous devons compter le nombre de façons de placer le bloc dans le cache, ce qui correspond à l'ordre de sortie des éléments \(\binom{M}{B}\) ou l'ordre dans lequel ils sont lus. Nous arrivons à la relation :

$$ (N \binom{M}{B})^{T} \geq \frac{N!}{B!^{\frac{N}{B}}} $$

Maintenant, en prenant le logarithme des deux côtés et en appliquant la formule de Stirling, on obtient :

$$ T = \Omega(\frac{N}{B} \log_{\frac{M}{B}} \frac{N}{B}) $$

Il ne reste donc plus qu'à déterminer ce mystérieux \(N\) (présent dans la fonction min). Il correspond simplement à l'algorithme de permutation classique du modèle RAM, où on ne prête pas attention à ces notions de blocs. Nous verrons par la suite que des algorithmes de tri présentent une complexité supérieure (\(O(.)\)) dans cette même borne, et sont donc optimaux en ce sens (\(\Theta(.)\)).

Algorithmes primordiaux

Nous allons commencer par aborder les algorithmes primordiaux. Ceux-ci servent généralement de primitives pour de nombreux autres algorithmes et leur étude fournit donc une base solide pour traiter des problèmes plus complexes. Il est donc d'autant plus important d'avoir des algorithmes efficaces pour ceux-ci.

Parcours

Le parcours (scanning) est l'opération de base qui consiste simplement à consulter chacun des éléments d'une collection contiguë en mémoire. Naturellement, sa complexité est limitée par \(O(\frac{N}{B})\). Il en va de même si nous exécutons plusieurs parcours en parallèle, comme lors d'une inversion de l'entrée, par exemple. Cette complexité correspond à ce qu'on peut s'attendre de la linéarité dans un tel modèle, de même \(O(\frac{1}{B})\) est l'équivalent du temps constant pour un élément.

Recherche

La recherche d'un élément dans une collection triée bénéficie relativement peu de ces notions de blocs. En effet, nous pouvons utiliser un argument lié à la théorie de l'information, s'il y a \(N\) éléments, notre élément peut être trouvé n'importe où dans ces \(N\) positions, donc nous avons besoin de \(\Omega(\log N)\) bits d'information (pour encoder la position). Or, quand nous lisons un bloc, nous obtenons \(\Omega(\log B)\) bits d'information à la fois, puisque chaque bloc lu révèle atomiquement où se trouve l'élément de requête parmi ces \(B\) éléments, ceci conduit à \(\Omega(\frac{\log N}{\log B}) = \Omega(\log_{B} N)\). Les B-trees représentent une solution à ce problème.

Partitionnement multiple

Le partitionnement multiple consiste à fractionner un ensemble de \(N\) éléments non triés en \(d\) paquets de telle sorte que tous les éléments du \(i\)e paquet soient plus petits que le \(i\)e pivot et plus grands que le \(i-1\)e pivot étant donné une liste de \(d-1\) pivots triés dans l'ordre croissant.

L'idée est tout à fait naturelle. Nous effectuons \(\frac{d}{B}\) parcours où on compte le nombre d'éléments plus petit ou plus grand pour chacun des pivots. Ensuite, il suffit de combiner ces informations (all-prefix-sum / scan pour les haskelliens - si le premier pivot possède \(x\) valeurs et le second \(y\), le troisième pourra écrire à partir de la position \(x+y\)) afin de déterminer à quel index nous pourrons écrire sans conflits les éléments relatifs à un pivot. Ceci aboutit à une complexité en \(O(\frac{N}{B})\).

Sélection

De manière analogue, étant donné un ensemble non ordonné de taille \(N\) et un entier \(k\) (avec \(1 \leq k \leq N\)). Le problème de sélection consiste à trouver un élément tel qu'il est plus grand que tous les \(k - 1\) éléments précédents.

L'idée est assez similaire à celle du « k-th sort ». Nous effectuons un partitionnement multiple sur les entrées et effectuons la récursion sur le sous-ensemble ciblé. Cela conduit à une complexité équivalente au problème précédent, soit \(O(\frac{N}{B})\).

Tri fusion

Complexifions l'exercice et attaquons-nous maintenant à un algorithme de tri et à la complexité du tri fusion classique (merge-sort), c'est-à-dire avec la fusion de deux listes à la fois. La complexité est décrite par le système ci-dessous :

$$ \left\{ \begin{array}{ll} MT(N) = 2MT(\frac{N}{2}) + O(\frac{N}{B}) \\ MT(M) = O(\frac{M}{B}) \end{array} \right. $$

En effet, nous effectuons à chaque fois deux récursions, et au retour de celle-ci, nous fusionnons les résultats de celles-ci en une seule liste. Nous devons donc effectuer un parcours simultanément afin de produire notre résultat, donc \(O(\frac{N}{B})\). Maintenant, remarquons que la hauteur de la récursion est bornée par \(O(\log N - \log M) = O(\log \frac{N}{M})\) puisqu'une fois que nous arrivons à la taille du cache, les opérations deviennent essentiellement gratuites. Finalement, la quantité de travail reste la même pour chacun des niveaux de l'arbre de récursion, on crée deux sous-problèmes mais de moitié taille, ce qui conduit à \(O(\frac{N}{B} \log \frac{N}{M})\).

Seulement, ce n'est pas optimal. En effet, nous n'utilisons pas à pleines capacités la taille du cache. Au lieu de fusionner deux listes à la fois, nous pourrions en fusionner jusqu'à \(\frac{M}{B}\) à la fois (nous précisons que l'algorithme n'est pas trivial). Il suffit de remplacer le coefficient « \(2\) » par \(\frac{M}{B}\) et nous retombons sur la borne optimale, soit \(O(\frac{N}{B} \log_{\frac{M}{B}} \frac{N}{B})\).

Tri par distribution

Le tri par distribution consiste à partitionner un ensemble de \(N\) éléments non triés en \(d\) paquets, chacun étant trié et concaténé de façon récursive pour obtenir le résultat final, il peut être considéré comme une généralisation du tri rapide (quick-sort). L'algorithme, par lui-même, échantillonne au hasard des éléments des données pour obtenir \(\sqrt{\frac{M}{B}}\) pivots, partitionne les données et s'appelle lui-même sur ces sous-ensembles. Quand il n'y a plus assez de données pour en recréer un autre, nous effectuons un tri classique et optimal en mémoire interne.

Certains problèmes sélectionnés

Il existe une quantité astronomique de problèmes étudiés dans ce modèle de calcul, nous en avons sélectionné certains qui nous semblaient plus remarquables ou intéressants. Nous sommes très loin d'être exhaustifs.

Algorithmes sur les matrices

Lorsqu'on considère des algorithmes sur les matrices, il est nécessaire de considérer la manière dont les éléments sont positionnés en mémoire. Pour les matrices denses, on distingue généralement trois formes :

• Par colonne : les éléments sont d'abord ordonnés par colonnes et puis par lignes et ce dans une même colonne.
• Par ligne : les éléments sont ordonnés par lignes et puis par colonnes.
• Récursif ou zig-zag : cette disposition particulière est souvent employée afin de construire des algorithmes optimaux. De nombreux théorèmes impliquent une courbe remplissant l'espace de manière récursive afin de déterminer l'ordre des éléments. Certains reconnaîtront là la disposition dite en Z.

Transposition de matrice

Transposer une matrice \(N = N_{x} * N_{y}\) requiert \(\Theta(\frac{N}{B} \log_{\frac{M}{B}} \text{min} \{ M, N_{x}, N_{y}, N \})\).

Ce résultat n'est pas tellement étonnant, il faut se convaincre qu'une transposition de matrice est un cas particulier de permutation, surtout lorsque \(B\) est relativement grand (\(\approx \frac{1}{2} M\)) et \(N\) est en \(O(M^{2})\). Pour des \(B\) plus petits, la structure spéciale de la permutation associée à la transposition rend l'opération plus simple. En effet, la matrice peut être divisée en sous-matrices qui contiennent \(B^{2}\) éléments, afin que chaque sous-matrice contienne \(B\) blocs en ligne ainsi que \(B\) blocs en colonne. Ainsi, si \(B^{2} < M\), la transposition peut être effectuée en une seule passe en transposant les sous-matrices directement en mémoire interne.

Mais ce n'est peut-être pas le résultat principal. En effet, la transposition de matrice est également un cas particulier d'une classe plus générale de permutations et dites « bit-permute/complement » (BPC), qui est lui-même un sous-ensemble des « bit-matrix-multiply/complement » (BMMC). En résumant de manière très concise, il est possible d'exprimer les permutations en termes d'une matrice de permutations (pas forcément unitaire). Cette forme est également capable d'exprimer d'autres problèmes, notamment les problèmes posés sur des DAG. Cormen et al.¹ ont obtenu un résultat prodigieux :

Le nombre de transferts requis pour effectuer une permutation BMMC définie par une matrice \(A\) et un vecteur \(c\) est :

$$ \Theta(\frac{N}{B} (1 + \frac{rank(\gamma)}{\log \frac{M}{B}})) $$

où \(\gamma\) est la sous-matrice \(\log \frac{N}{B} \times \log B \) située dans le coin inférieur gauche de \(A\). Ce résultat peut sembler anecdotique, mais représente une avancée majeure. Jusqu'à présent, la complexité était essentiellement démontrée de manière « existentielle », c’est-à-dire qu'il existait au moins une instance du problème qui nécessitait cette complexité. Ici, le résultat est dit « universel », la complexité est déterminée par une catégorisation de l'instance du problème.

Multiplication de matrices

Si nous appliquons l'algorithme classique de multiplication de matrices, avec la première en ligne et la seconde en colonne nous devrions, pour chacun des éléments, effectuer deux parcours, ce qui aboutirait à une complexité en \(O(\frac{N^{3}}{B})\), ce qui n'est pas optimal. En effet, il est possible d'atteindre \(\Theta(\frac{N^{3}}{B\sqrt{M}})\)², ce qui coïncide avec le résultat de Hong et Kung. Il faut remarquer que lors d'une multiplication classique, les mêmes lignes et colonnes sont lues de nombreuses fois, ce qui est évidemment inefficace. La solution consiste à stocker les éléments des matrices de manière récursive, chaque fois subdivisant les quatre coins les uns après les autres afin d'obtenir une disposition proche de : \(\text{layout}(Z) = \text{layout}(Z_{11})\text{layout}(Z_{12})\text{layout}(Z_{21})\text{layout}(Z_{22})\).

La complexité est décrite par ce système : $$ \left\{ \begin{array}{ll} MT(N) = 8MT(\frac{N}{2}) + O(\frac{N^{2}}{B}) \\ MT(\sqrt{\frac{M}{3}}) = O(\frac{M}{B}) \end{array} \right. $$

En effet, chaque coin de la matrice résultante peut être obtenu comme la somme du produit des deux sous-matrices, comme il existe 4 coins avec 2 produits (\(Z_{11} = X_{11}*Y_{11} + X_{12}*Y_{21}\)), nous avons 8 récursions. Les sommations sont indépendantes de la récursion et coûtent \(O(\frac{N^{2}}{B})\) vu que nous devons effectuer le parcours en \(X\) et en \(Y\). Finalement, lorsque les matrices peuvent être entièrement contenues dans la mémoire interne, et qu'elles sont stockées de manière continue, le pire cas consisterait à parcourir chacun des blocs, \(O(\frac{M}{B})\). Maintenant, grâce au Master Theorem, nous devons compter le nombre de feuilles puisque le coût de la somme est plus petit que celui de la récursion, il y a donc \(8^{\log N / \sqrt{M / 3}} = (N / \sqrt{M / 3})^{3}\) feuilles. Le coût total est donc déterminé par :

$$ (\frac{N}{\sqrt{M / 3}})^{3} O(\frac{M}{B}) = \Theta(\frac{N^{3}}{M^{3/2}}) O(\frac{M}{B}) = \Theta(\frac{N^{3}}{B\sqrt{M}}) $$

Algorithmes sur les graphes

Les algorithmes sur les graphes représentent une vraie difficulté pour l'I/O complexité. En effet, des algorithmes optimaux, par rapport au modèle RAM, ne semblent pas toujours possibles. Chiang et al.³ ont d'ailleurs conjecturé une certaine équivalence entre les complexités liées à l'I/O et le parallélisme, suite aux nombreux problèmes facilement parallélisables issus d'algorithmes I/O.

Classement de liste

Étant donné une liste d'éléments \(N\), chacun identifié par une adresse unique (identifiant) et pointant vers son successeur. Le but est de définir le rang de chaque élément, où le rang correspond au nombre d'éléments entre la tête de liste et l'élément.

Étonnamment, la complexité du classement de liste est en \(\Theta(\frac{N}{B} \log_{\frac{M}{B}} \frac{N}{B})\) et est donc aussi complexe que de trier une collection en raison de la difficulté de transférer l'information et de son lien étroit (et loin d'être évident) avec le problème de permutation.

L'idée principale consiste à créer des ensembles indépendants via 3-coloring (sous-ensembles de taille \(\frac{N}{3}\)) et son algorithme des arêtes avant/arrière ou via un tirage au sort déterministe (sous-ensembles de taille \(\frac{N}{4}\), « deterministic coin tossing »), résoudre les sous-problèmes et recomposer la solution. Cette opération de décomposition et de reconstruction de la liste est appelée brigde-out/in, elle consiste à faire une copie de la liste originale, à trier la liste originale par l'identifiant du successeur, à parcourir l'original et la copie en même temps pour obtenir l'information sur le successeur et à trier de nouveau la liste originale modifiée par son identifiant.

3-coloring peut être fait comme suit, on colore alternativement les pointeurs avant en rouge et bleu, et en arrière, en vert et bleu (chaque nœud aura une couleur à l'exception de tête/queue qui peuvent en avoir deux), il ne reste plus qu'à les colorier de la couleur de la tête de liste. En pratique, nous devons mettre les nœuds dans une file à priorité basée sur l'index, parce que nous ne pouvons accéder aux éléments dans n'importe quel ordre, cela entraînerait trop de transferts, et une file à priorité peut avoir une complexité en \(O(\frac{1}{B}\log_{\frac{M}{B}} \frac{N}{B})\) par élément et par opération (Buffer-tree).

Tour eulérien

Le problème précédent vous aura sans doute paru quelque peu nébuleux. Mais il est employé comme base pour de nombreux algorithmes et est souvent combiné avec la notion de tour eulérien. Le tour eulérien a été introduit par Robert E. Tarjan et Uzi Vishkin⁴, il est défini comme étant capable de faire le tour d'un graphe en visitant chaque arête exactement deux fois, et ce, dans les deux directions. L'idée sous-jacente est que nous pouvons employer un algorithme de type all-prefix-sum (ou scan) sur le tour eulérien. Ceci permet de représenter des graphes comme des collections plates d'éléments et ainsi appliquer nos techniques plus avancées. La conséquence est également qu'un arbre peut être traité d'une même manière, bien qu'il soit dégénéré sous la forme d'une liste.

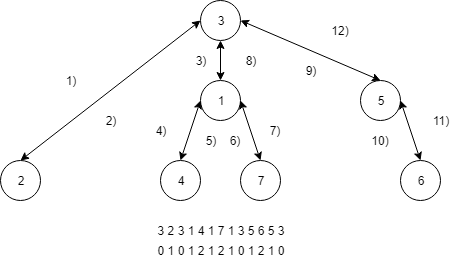
Par exemple, le problème du plus petit ancêtre commun (lowest common ancestor - LCA), qui consiste à, étant deux nœuds \(v\) et \(w\) dans un arbre \(T\), trouver le nœud le plus bas dans l'arbre qui possède \(v\) et \(w\) comme descendants. Ce problème peut également être réduit à celui de requête du plus petit dans un intervalle (range minimum query - RMQ). Dans l'exemple suivant, nous effectuons un parcours préfixe où nous notons les nœuds visités d'un part et la profondeur associée d'autre part. Par exemple, le LCA de 7 et 5 revient à chercher le RMQ dans l'intervalle associé : 2101, la réponse est donc 0, soit le nœud 3.

Techniques généralistes sur les graphes

Vous pouvez aisément imaginer que déterminer l'I/O complexité sur des graphes posent quelques problèmes. On peut imaginer des réductions vers des problèmes de matrices par le biais des matrices d'adjacence mais la complexité en pâtirait très certainement. Certains outils et techniques ont été développés afin d'étudier ces problèmes. Généralement, il s'agit d'extensions de notions algorithmiques avancées. Nous ne ferons, encore une fois, qu'effleurer un sujet tellement vaste.

Une bonne partie des algorithmes sur les graphes se reposent sur la construction d'une structure de données auxiliaires afin de résoudre le problème. La clef réside dans ces fameux Buffer (repository) tree (BRT) qui correspondent grossièrement à de simples B-tree, où un buffer d'opérations est ajouté à chaque nœud afin d'amortir son coût. Celles-ci sont donc effectuées uniquement lorsque ce buffer est rempli. On peut prouver que la complexité amortie d'une insertion est bornée par : \(O(\frac{1}{B}\log_{\frac{M}{B}} \frac{N}{B})\) et d'une extraction l'est par : \(O(\log_{\frac{M}{B}} \frac{N}{B} + \frac{S}{B})\) où \(S\) désigne la taille de l'ensemble retourné⁵.

Parcours en profondeur sur un graphe dirigé

Nous pouvons maintenant étudier la complexité d'un directed DFS. Nous commencerons par rappeler qu'un DFS consiste à placer sur la pile le premier sommet, ajouter ceux adjacents et qui n'ont pas déjà été visités et recommencer la procédure avec le sommet de la pile jusqu'à ce qu'elle soit vide. Les opérations de pile coûtent naturellement (et de manière amortie) \(O(\frac{1}{B})\) par élément (le problème consiste donc à trouver les sommets non visités). L'astuce consiste à introduire deux autres structures de données, un Buffer tree qui s'occupera de stocker toutes les arêtes \((v, w)\) par la clef \(v\) et une file à priorité par sommet afin de conserver les arêtes sortantes non encore explorées. L'invariant consiste à ce que, à tout instant et ce pour chaque sommet, les arêtes présentent dans la file à priorité et absentes du Buffer tree pointent vers des sommets non visités.

Cet algorithme s’ensuit à chaque fois qu'on possède un nouveau sommet \(v\) (le premier ou sur la pile) :

• On commence par extraire toutes les arêtes ayant pour clef \(v\). \(O(|V| \log_{\frac{M}{B}}\frac{|E|}{B} + \frac{|E|}{B})\)
• On supprime ces arêtes des files à priorité. Celles-ci conservent alors uniquement des arêtes vers des sommets non visités. \(O(|V| + \text{sort}(|E|))\)
• Si la file à priorité du sommet \(v\) est vide, il faut revenir en arrière dans le parcours (extraction du sommet de la pile).
• Sinon, on extrait le minimum de la file à priorité liée à \(v\) et on se retrouve avec l'arête \((v, w)\). \(O(\text{sort}(|E|))\)
• On place \(w\) sur la pile. \(O(\frac{|V|}{B})\)
• Les arêtes menant à \(w\) sont recherchées \((x, w)\) et insérées dans le Buffer tree selon \(x\). \(O(\frac{|E|}{B} \log_{\frac{M}{B}} \frac{|E|}{B}))\)

$$ O((|V| + \frac{|E|}{B}) \log_{\frac{M}{B}} \frac{|E|}{B})) $$

L'algorithme est essentiellement le même dans le cas d'un parcours en largeur même si les files à priorité ne sont plus indispensables puisqu'on visite les sommets exactement une fois. ;) Étonnamment, sur un graphe non dirigé, un BFS peut être effectué en \(O(|V| + \text{sort}(|E|))\) de manière déterministe et dans des complexités étranges (fonction du diamètre du graphe) de manière (plus ou moins) non déterministe⁶.

Plus court chemin

Une autre avancée majeure fut la résolution des problèmes de plus courts chemins. Et notamment, celui à source unique (SSSP) et qui correspond à Dijkstra. L'idée était d'introduire des Tournament tree⁷, suite au fait que les Buffer tree ne peuvent supporter l'opération de réduction des clefs (DecreaseKey), essentielle à l'algorithme. Ils ont l'avantage de supporter cette fameuse opération mais ajoutent un surcoût de \(\log_{2} \frac{M}{B}\) aux opérations (par rapport au Buffer tree). Brièvement, ce tournament tree est un arbre binaire fixe avec \(\frac{N}{M}\) feuilles et, à chaque nœud, on retrouve un buffer de taille \(M\) qui contient tous les éléments ayant une priorité plus faible dans le sous-arbre. Il existe également un buffer qui permet d'effectuer des signaux pour mettre à jour les clefs.

Il suffit ensuite d'appliquer l'algorithme classique sur cette structure de données. Seulement, il y aurait un petit problème et une modification doit y être apportée afin d'obtenir une meilleure complexité. En effet, Dijkstra demande de vérifier si un des sommets voisins est terminal afin d'effectuer l'opération de réduction des clefs. La solution consiste à introduire une opération de mise à jour sur les voisins directs (excepté le parent) mais ceci entraîne un nouveau problème lié à la seconde visite d'un même sommet⁷. Bref, c'est compliqué. ^^ Au final, il est quand même possible d'obtenir :

$$ O(|V| + \frac{|E|}{B} \log \frac{|E|}{B}) $$

Autres notions

De nombreux autres notions et outils ont été créés en algorithmique afin de répondre à moult questions. Nous penserons notamment au partitionnement de graphes, qui a permis d'aider au problème de SSSP sur des graphes planaires⁸. Au ratissage et compressage (rake and compress) introduit dans un très long article originellement pour le parallélisme⁹. Ou encore, une notion connexe appelée : block-cut point tree et qui possède certaines structures mathématiques intéressantes¹⁰.

Nous terminerons par insister sur le fait que nous n'avons en aucun cas abordé la notion de complexité optimale pour ces algorithmes. Ceux-ci sont encore sujets à de nombreuses questions et certaines bornes théoriques restent encore très floues et fort dépendantes de la structure du graphe. Cela reste des problèmes ouverts.

Cache-oblivious

Lorsqu'on aborde les thèmes liés à l'I/O complexité, le modèle cache-oblivious émerge comme un véritable chef d'œuvre. Introduit en 1999 par Matteo Frigo, Charles E. Leierson, Harald Prokop et Sridhar Ramachandran¹, il est semblable au modèle EM mais propose une différence fondamentale. On ne connaît ni la taille de \(B\) ni de \(M\), ces éléments seront employés a posteriori pour analyser la complexité de l'algorithme, l'algorithme n'en a pas conscience. Cette notion est très forte parce qu'elle implique que l'algorithme est optimal de manière globale et donc sous n'importe quelle circonstance, peu importe les valeurs de \(B\) ou de \(M\). Cette notion d'obliviousness a évidemment été portée à d'autres complexités (temporelle ou réseau).

Nous allons parcourir brièvement certains résultats issus de ce modèle afin de vous donner l'essence de la beauté mais nous ne nous attarderons pas en profondeur.

Parcours

Parcourir \(N\) éléments reste en \(O(\frac{N}{B})\). Seulement, il devient plus difficile d'en effectuer plusieurs en parallèle puisque nous ne connaissons pas la taille du cache. Des petites constantes sont donc envisageables.

Recherche

Pour rechercher un élément dans une collection triée, nous pourrions employer un B-tree. Seulement, celui-ci n'est plus optimal dans ce modèle de calcul, pas sans modification.

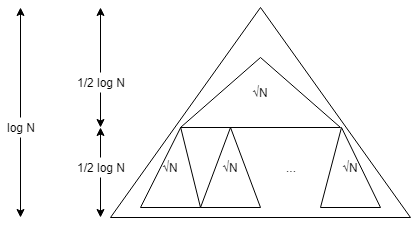
L'idée est de créer un arbre binaire (puisque nous ignorons \(B\)) et de diviser récursivement les données de sorte que le sommet contienne \(\sqrt{N}\) éléments et que les \(\sqrt{N}\) restes contiennent les \(\sqrt{N}\) données. Nous stockons le sommet et puis chacun des enfants à la suite en mémoire. Nous effectuons cette opération de découpage jusqu'à des éléments uniques, cette disposition est qualifiée de Van Emde Boas. Entre temps, nous aurons croisé des sous-ensembles ayant une taille légèrement inférieure ou égale à \(B\). La question consiste à se demander combien de triangles de taille au maximum \(B\) doit-on traverser afin d'atteindre les feuilles ? Nous savons que la taille de ceux-ci est au moins \(\frac{1}{2} \log B\) puisqu'en subdivisant, on risque de rater la taille de \(B\) d'un facteur de 2. Ensuite, chaque bloc peut être mal aligné et être placé à l'intersection de 2 blocs. Au final, nous obtenons \(O(4 \log_{B} N)\). Il est toutefois possible de décrire des B-trees dynamiques atteignant la borne optimale².

Tri fusion

Il est possible de définir l'équivalent du tri fusion dans un modèle cache-oblivious. L'algorithme s'appelle le « funnel sort » et se base sur la construction de « funnel » qui permette de fusionner \(k\) listes triées de taille \(\Theta(k^{3})\) en \(O(\frac{k^{3}}{B} \log_{\frac{M}{B}} \frac{k}{B} + k)\).

L'idée est assez farfelue, on définit récursivement les funnels comme étant composé de sous-funnels. De telle sorte qu'on arrive au final à la fusion de 2 listes simples. La récursion est toujours la clef en algorithmique !

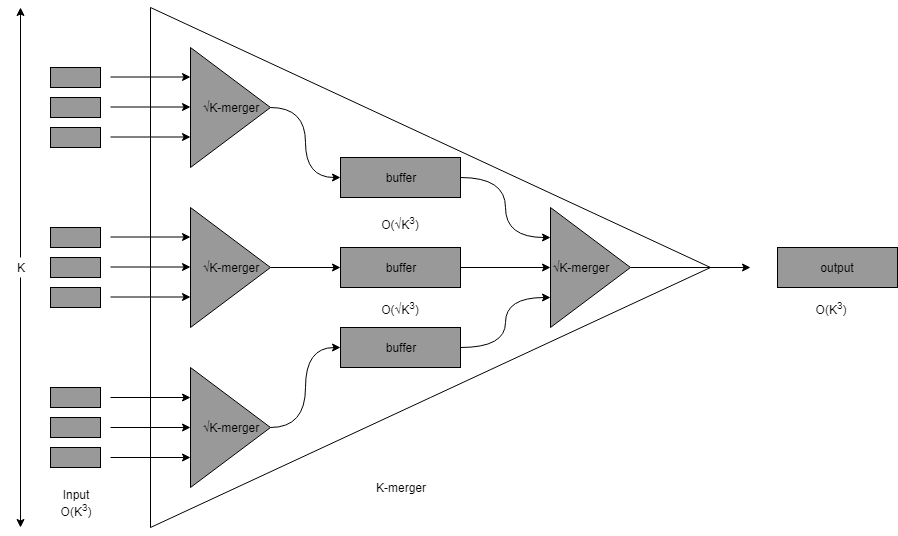
Un peu de recul

Le modèle cache-oblivious est simple et élégant. En s'affranchissant explicitement des paramètres relatifs au cache, on obtient des résultats très généraux et les algorithmes deviennent optimaux par rapport à n'importe quelle configuration. Cela permet, par la même occasion, de supprimer les problèmes qui émergent avec des hiérarchies de caches d’un seul tenant puisqu’on sait que la situation est optimale entre chaque paire.

En pratique, on connaît (ou tout du moins, on a des bonnes idées sur) la configuration sur laquelle on va faire tourner l’algorithme. On peut donc affiner au mieux les paramètres de l'algorithme EM et battre les cache-oblivious. On peut d'ailleurs tenter de quantifier le gain d’information théorique que l’on a lorsqu’on connaît les paramètres du problème a priori mais il est somme toute faible².

Seulement, le problème majeur est que les algorithmes cache-oblivious sont des monstruosités à programmer alors que les EM sont nettement plus commodes à implémenter. La récursivité est un point crucial pour ce type d'algorithmes et permet d'offrir des solutions d'une simplicité remarquable à des problèmes pourtant complexes. Mais ces belles récursions entraînent des détails d'implémentation très techniques. Pour s’en convaincre, il suffit d’écrire un algorithme qui fusionne un nombre arbitraire de listes triées, on se confronte très vite à un mur.

Conclusions

Nous l'avons vu, ce modèle de calcul, initialement introduit comme curiosité, présente une vraie profondeur et de nombreuses difficultés sujettes à d'importantes recherches. Les algorithmes I/O sont généralement fort différents de ceux s'intéressant aux aspects temporaux et présentent souvent des solutions élégantes. L'un des points forts de ce modèle est que les algorithmes peuvent souvent être modifiés afin d'incorporer du parallélisme de manière plus simple, une meilleure séparation des données introduisant moins de problème de concurrence.

Ils visent donc à répondre à différentes problématiques:

• Les données sont trop grandes pour être traitées directement en mémoire, il faut donc les charger petit à petit et éviter d'effectuer trop de transferts avec des bases de données qui peuvent, peut-être, être situées à l'autre bout du monde.
• Les opérations mémoires ont un coût, accéder aux éléments de manière aléatoire prend plus de temps que de manière séquentielle. Charger les données par bloc permet d'économiser le nombre d'accès et il est fort probable que l'on souhaite accéder aux donnés adjacentes, comme dans le cas d'une boucle for.
• Ce modèle considère que les opérations du côté CPU n'ont pas de coût. Cette hypothèse est forte mais supportée par le fait que certaines opérations peuvent être effectuées en une demie nanoseconde côté CPU alors que chercher des données sur le disque dur peut prendre plusieurs millisecondes, cela représente un facteur un million !
• Étudier un algorithme sous un autre aspect permet de mieux le connaître. Ceci permet également de définir des nouvelles notions de complexité, est-ce qu'un algorithme optimal de manière temporelle et de manière I/O est-il encore plus optimal ? Est-ce qu'il existe une équivalence simple entre ces modèles de calcul et ceux temporaux ? Une réponse à cette dernière question a été présentée récemment et la réponse, assez positive, est exceptionnelle¹.

L'idéal est donc de trouver des algorithmes optimaux dans plusieurs modèles comme le merge-sort ou les B-trees. Seulement, les algorithmes I/O ont tendance à introduire une complexité d'implémentation qui peut se traduire par une lenteur dans les modèles temporels, c'est surtout le cas pour les algorithmes ayant attrait aux graphes. Et ce qui intéresse les gens est essentiellement le temps d’exécution. La situation est d’ailleurs très claire avec le « list ranking problem », en complexité temporelle, on a un bête algorithme (il suffit de parcourir la liste) en \(O(N)\) (thèse de James C. Wyllie², inventeur du modèle PRAM). Alors que si on tente de le rendre optimal en EM, la complexité temporelle passe à un \(O(N \log N)\)³.

J'espère que vous aurez vu la beauté qui peut se cacher sous un tel sujet, bien qu'il soit abordé de manière si brève. Si vous désirez aller plus loin, je vous invite à suivre les travaux de Jeffrey S. Vitter, auteur de moult travaux dans ce domaine. Les cours de Erik Demaine disponibles sur le site du MIT, notamment relatifs à la notion de cache-oblivious, sont également des petites merveilles (le MIT produit et diffuse des cours dans des domaines très variés et faisant preuve d'une extrême qualité). Il est également intéressant de lire les travaux originaux et ceux plus modernes. Finalement, et plus récemment avec l'avènement des GPU, le modèle PEM (parallel external memory) a gagné en intérêt vu une similitude relativement adéquate. Brièvement, ce modèle combine naturellement le modèle EM avec les notions de parallélisme, les résultats qui en découlent sont vraiment naturels.

Remerciements

• Merci à @Quentin pour sa lecture et ses propositions de points à améliorer et à clarifier.
• Je tiens également à remercier @Taurre pour sa relecture attentive et ses corrections apportées sur la forme.
• Finalement, au « Algorithms Research Group » de l'Université Libre de Bruxelles (U.L.B.) et ses membres exceptionnels pour m'avoir appris l'esthétisme en informatique.