Introduction

Dans cet article, nous allons présenter une étude de cas pour un problème concret qui trouve ses origines dans la fraude fiscale. Il s’agit des sanctions économiques, véritables armes géopolitiques menant à de très lourdes condamnations en cas de non-respect. En effet, ces sanctions sont la version moderne des embargos économiques et trouvent leur place dans le contexte de ces dernières années, où la lutte contre l’évasion fiscale est devenue un enjeu majeur au travers des notions telles que la lutte contre le blanchiment d’argent (anti money laundering ou AML) ou la connaissance du client (know your customer ou KYC). Plus récemment, on a commencé à entendre parler d’imposition au niveau mondial ou d’obligations de transparence par rapport aux montages financiers.

Nous commencerons par énoncer le problème à l’origine de cette étude de manière plus concrète, en présentant d’abord le contexte politique lié aux sanctions économiques et les règles mises en place. Quels sont les enjeux et à quoi vaut-il mieux prêter attention. Nous expliquerons son abstraction la plus classique ainsi que les solutions existantes à cette problématique. Ensuite, nous reviendrons sur des aspects plus "ingénieurs" liés à l’implémentation et aux données réelles.

La lecture de cet article fait l’hypothèse d’une certaine compréhension de l’informatique et de la programmation en vue d’être suffisamment à l’aise avec les concepts et leurs implications. Il cherche donc à s’adresser principalement à des gens ayant un niveau supérieur à celui du bachelier (licence pour nos amis français), même si la matière vue ici ne sera pas particulièrement avancée ou à la pointe de la recherche. Nous recommandons également d’avoir de bonnes notions de calcul matriciel.

Cet article présentera, également, essentiellement les notions du droit européen. Mais les grands principes restent les mêmes pour les autres puissances: la Chine, les États-Unis, la Russie, les Émirats Arabes Unis, l’Union Africaine, … Les principales différences résident dans la définition des grands "méchants" et dans les notions de propriété et de contrôle sur lesquels nous reviendrons.

Définition du problème

Contexte juridique et aspects institutionnels

Nombreux organismes internationaux ou nationaux agissent et contribuent à la mise en œuvre, l’application et au contrôle des mesures restrictives (au sens global de sanctions). C’est ce qu’on appelle communément l’appareil idéologique de l’État. Le monde politique ou judiciaire peut déployer des instruments juridiques envers des pays tiers, des entités (morales) ou des particuliers (en accord avec le chapitre VII de la Charte des Nations unies énoncée par le Conseil de sécurité des Nations unies - CSNU). Et, ces institutions peuvent également être proactives et aller au-delà des recommandations des Nations unies. Ces instruments juridiques, imposant des mesures restrictives, peuvent renvoyer à des incitations destinées à encourager les changements nécessaires de politique ou à réprimander des activités considérées comme amorales et illégales.

Ces sanctions visent avant tout à marquer une prise de position franche par rapport à la politique étrangère, sans passer par des mesures de rétorsion militaires. Ces armes juridiques consistent en:

• Des embargos sur les armes ou sur le matériel permettant de contenir une répression interne.
• Des restrictions à l’importation ou l’exportation.
• L’impossibilité d’assistance technique qui se traduit par l’interdiction d’aide, de support ou de collaboration avec les entités concernées¹.
• Des restrictions sur les admissions (interdiction de voyager - de vols), cadre des "sanctions diplomatiques".
• Il est également possible d’interrompre, ou à défaut de limiter, les relations économico-financières d’une entité que ce soit par le gel d’avoirs, l’interdiction de commerce, de financements ou d’investissements.

Au niveau européen, les sanctions concernent²:

• Des États (non-européens) en raison de leurs politiques (démocratie, droits de l’Homme, non-prolifération d’armes de destruction massive, expansionnisme).
• Des groupes ou organisations, essentiellement pour des raisons de terrorisme.
• Des personnes, que ce soit par leur implication directe dans la politique, ou par le biais d’activités illégales: terrorisme, traite d’êtres humains, …
• Des entités (entreprises) fournissant les moyens de mener les activités précédemment mentionnées.
• En outre, une entité dont le siège social est établi dans un État membre de l’Union européenne (UE) ne peut pas, entre autres, utiliser une société qu’elle contrôle comme un instrument lui permettant de contourner une interdiction, y compris lorsque cette société n’est pas établie dans l’UE.

Propriété et contrôle

Mais comment peut-on faire pour déterminer quelles sont les entreprises qui dépendent d’un État de celles indépendantes ? Pour cela, on distingue les notions de propriétés et de contrôles, il est d’ailleurs possible d’avoir le contrôle sur une entité en ne possédant qu’une "minorité" de sa propriété ou d’être majoritairement propriétaire sans avoir le contrôle sur l’entité.

Selon le règlement du Conseil européen³:

La propriété est définie comme le fait de posséder au moins 50% des droits de propriété d’une entité ou de détenir une participation majoritaire en son sein. À noter que les termes se veulent (volontairement ?) vagues. Parle-t-on de majorité absolue ou relative, quid de l’usage d’intermédiaires pour détenir une société ?

La notion de contrôle est encore plus complexe. Chaque entreprise peut définir son propre système de contrôle (ce qui a évidemment des impacts sur la propriété de celle-ci). Afin de définir ce critère, on cherche à voir si l’entité sujette possède l’un des critères suivants:

La possibilité de nommer, constituer ou révoquer la majorité du comité de direction de l’entreprise, son board. L’exercice d’une influence dominante sur la personne morale (par le biais d’un accord avec les autres actionnaires) de manière directe ou non (par l’intermédiaire éventuel de sociétés-écrans). Le fait de disposer d’une partie des actifs d’une société, ou de répondre aux obligations financières de celles-ci (en étant garant ou en consolidant ses comptes). Évidemment, il n’est pas question de "magiquement" faire disparaître la sanction en changeant la responsabilité au travers d’un homme de paille (que ce soit par l’usage d’une société-écran ou en nommant un parent de la personne condamnée à la tête).

Sur des exemples concrets, (not-)sanctioned représente une entité (non-)sanctionnée, les flèches en solide représentent le pourcentage de détention directe. Et, en rouge, vous avez la liste des entités "sanctionnées par extension", par application de la règle.

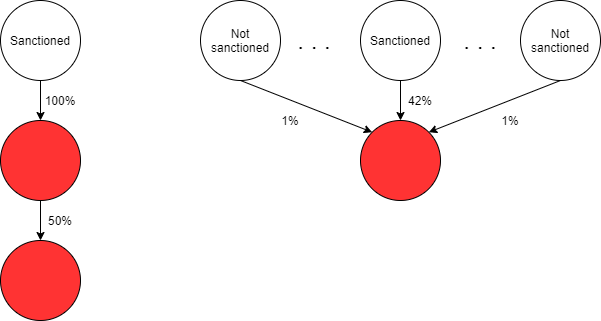
Le cas à gauche correspond à la définition de la propriété alors que celui à droite répond à la notion de contrôle (si les autres actionnaires possèdent tous 1% par exemple).

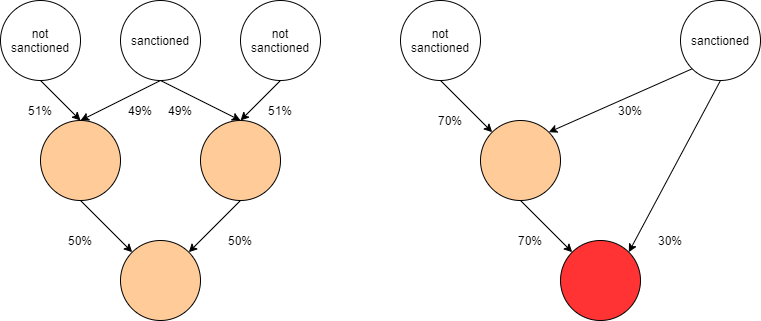
Ici, on rentre dans des cas nettement plus "discutables". En ce sens que l’entité sanctionnée ne possède ni le contrôle, ni la possession sur aucune de ses filiales. Le fait qu’une entité soit éventuellement considérée comme "sanctionnée par extension" est indiqué en orange. Seulement, en y regardant de plus près, on aperçoit quelque chose d’étonnant. Imaginons qu’on puisse combiner les pourcentages de détention des sociétés, si je possède une société A en direct à \(x\%\) et que A possède une société B en direct à \(y\%\), je peux estimer que je possède \(x\% \times y\%\) de B (de manière indirecte). D’autre part, si une société D est détenue par B et C à 50% que toutes les deux sont détenues à 100% (en direct) par la même entité A, on peut additionner les pourcentages indirects et dire que D est détenue à 100% par A. C’est ce qu’on appelle des pourcentages synthétiques de détention.

Dans notre exemple, pour le cas de gauche, nous aurions \( 49\% \times 50\% + 49\% \times 50\% = 49\% \( pour l’entité sanctionnée alors que la détention n’est que de 25,5% pour chacune des entités non-sanctionnées. De même, à droite, malgré que l’entité non-sanctionnée soit la plus grande propriétaire, l’entité sanctionnée possède \(30\% + 30\% \times 70\% = 51\%\) !

En l’occurrence, l’Union européenne reconnaît l’agrégation de pourcentages de détention directs, indirects et synthétiques. Donc, dans les cas évoqués précédemment, seul, le cas de droite est également "sanctionné par extension" en théorie.

Finalement, on peut aller encore plus loin et imaginer des situations encore plus discutables.

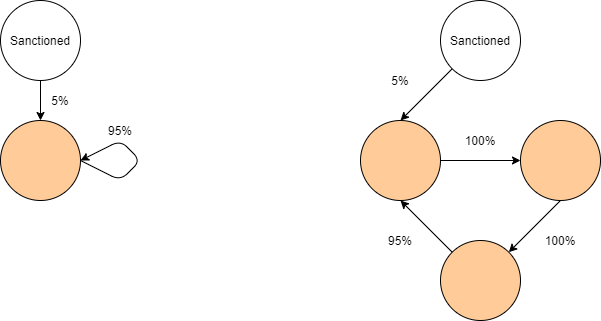
De nombreuses sociétés se détiennent mutuellement, que ce soit par de manière très directe (comme pour un certain conglomérat hongkongais aux initiales de "JM") ou de manière très indirecte (comme de nombreux fonds d’investissements). Comment alors déterminer à qui appartient la propriété réelle d’une société ou qui possède réellement le contrôle … On rentre dans un débat politique plus profond qui a pourtant une solution mathématique claire.

Chaînes de Markov

Pour rappel, une chaîne de Markov est un processus stochastique, à temps discret, où la prédiction future est entièrement contenue dans l’état courant (et donc qu’il n’y a pas de dépendances avec les états antérieurs ou futurs) - propriété dite de "Markov". Cette notion a été introduite par Andreï Markov au début du XXe siècle.

Chaque état d’une chaîne de Markov représente un événement, et les changements d’état du système sont appelés "transitions". On représente ces états comme les nœuds d’un graphe et les transitions comme des arêtes pondérées dont la somme des arêtes sortantes doit être égale à 1. Le processus est caractérisé par un espace d’états, une matrice de transition décrivant les probabilités de transitions particulières, et un état initial (ou une distribution initiale) à travers l’espace d’états.

>

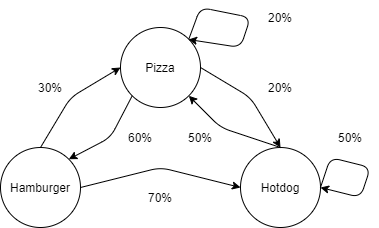
Par exemple, supposons que je ne mange que de la malbouffe et que je choisisse mon alimentation parmi trois plats: pizza, hamburger et hot-dog. Seulement, manger la même chose tous les jours est un peu triste à la longue. J’ai mis en place un ensemble de règles telles que lorsqu’on est le jour des hamburgers, j’ai 30% de chances de manger une pizza demain et 70% de manger un hot-dog. On peut associer la matrice de transitions (avec les probabilités associées aux transitions sortantes en ligne ou celles entrantes en colonne, dans l’ordre suivant: pizza, hamburger, hot-dog) suivante à cette chaîne de Markov que l’on nommera \(A\) par la suite:

$$ A = \begin{pmatrix} 0.2 & 0.6 & 0.2 \\ 0.3 & 0 & 0.7 \\ 0.5 & 0 & 0.5 \end{pmatrix} $$

Maintenant, imaginons que je parte de l'état "Hamburger" (on définit l'état initial \(\pi_0 = \begin{pmatrix} 0 & 1 & 0 \end{pmatrix}\)) et que je veuille savoir qu'elle est la probabilité que je mange de nouveau un hamburger dans 2 jours Je peux appliquer le calcul suivant:

Au premier jour, j'aurai:

$$ \pi_{0} * A = \begin{pmatrix}0.3 & 0 & 0.7 \end{pmatrix} = \pi_{1} $$

On obtient bien la probabilité de rejoindre les deux autres états depuis celui "hamburger". Et pour le second jour, j'aurai:

$$ \pi_1 * A = \begin{pmatrix}0.41 & 0.18 & 0.41 \end{pmatrix} = \pi_3 $$

La probabilité que je mange de nouveau un hamburger dans 2 jours est donc de: 18%.

Si l'on cherche à connaître la distribution à plus long terme, il faudra itérer ce processus autant de fois que nécessaire. On peut également s'intéresser à l'espérance, à la distribution finale qu'on aurait si on appliquait ce calcul une infinité de fois. Cela se traduit par l'équation:

$$ \pi * A = \pi $$

Cela rassemble terriblement à l'équation des valeurs propres d'une matrice (avec \(\lambda = 1\)). Seulement, avec une matrice \(n \times n\), vous aurez \(n\) valeurs et vecteurs propres (en prenant en compte les multiplicités). Il faut, en plus, imposer que la somme des composantes de \(\pi\) soit égale à 1. On appelle ce vecteur \(\pi\) final l'état stationnaire (steady state) du système.

Réduction

Une notion attachée au chaîne de Markov est la réduction. Une chaîne de Markov est dite "irréductible" s'il est possible de rejoindre chacun des états depuis n'importe lequel. Reprenons un cas classique où un état est absorbant et une fois atteint, on ne peut plus s'en échapper.

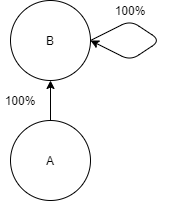
On aurait la matrice suivante:

$$ B = \begin{pmatrix} 0 & 1 \\ 0 & 1 \\ \end{pmatrix} $$

Si je pose \(\pi_0 = \begin{pmatrix} 1 & 0 \end{pmatrix}\), dès la première transition, je ne pourrai plus quitter l'actionnaire et l'état final restera à jamais: \(\pi = \begin{pmatrix} 0 & 1 \end{pmatrix}\). Cette chaîne est donc qualifiée de "réductible" (reducible).

La notion de réductibilité est importante parce qu'elle a des implications mathématiques sur le traitement des chaînes. Classiquement, on préférera décomposer le graphe en chaînes de Markov irréductibles où il est toujours possible de rejoindre n'importe quel état depuis un initial. Si la chaîne n'est pas réductible, il faudra appliquer les traitements adéquats pour prendre en considération les transitions "entrantes" du système, celles qui mènent à la situation d'une chaîne irréductible. Et, par contre, il faudra effectuer une autre démarche si le système possède des transitions "sortantes", celles qui quittent la chaîne irréductible vers des nouveaux états qui ne permettront pas un retour en arrière. Tous les nœuds faisant partie de la partie irréductible d'une chaîne de Markov sont qualifiés de transient.

Périodicité

Un autre point à considérer avec les chaînes de Markov est la notion de périodicité. On dit qu'une chaîne de Markov est périodique si l'on retombe sur le même état du système après \(n\) étapes, sinon, on dit qu'elle est apériodique. Prenons la matrice \(D\) suivante:

$$ D = \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} $$

Il semble assez clair que la situation va alterner entre deux états constamment \(D = D^2\). Alors qu'avec une autre matrice, prenons \(E\):

$$ E = \begin{pmatrix} 0.6 & 0.4 \\ 0.4 & 0.6 \\ \end{pmatrix} $$

Nous aurons toujours:

$$ \forall n E^{n} \neq E $$

La vision du problème sous la forme: \(\lim_{n \to \infty} A^{n}\) est intéressante puisqu'elle permet également d'avoir une idée de quel sera l'état stationnaire. En effet, chaque multiplication représente l'application d'une transition depuis une distribution. Chaque élément \(i, j\) représente la probabilité de transiter de l'état \(i\) vers l'état \(j\). Au final, on s'attend à ce que toutes les lignes se stabilisent vers certaines valeurs qui correspondent à l'état stationnaire. Notion évidemment modifiée si la chaîne est périodique.

Résolution et état stationnaire

La manière canonique de calculer l'état stationnaire du système (ou steady state) consiste à poser le système d'équations suivant:

$$ s_{i} = \sum_{k \in \text{transient}} a_{ki} s_{k} $$

La probabilité de se retrouver dans chacun des états \(s_{i}\) est exprimée comme une combinaison linéaire des probabilités de se retrouver dans un autre état de la chaîne \(s_{k}\) et d'emprunter la transition entre \(k\) et \(i\) et notée \(a_{ki}\).

De manière matricielle, le problème peut s'exprimer de cette manière:

$$ \begin{cases} \pi * A = \pi \\ \Vert \pi \Vert = \sum_{k \in \text{transient}} s_{k} = 1 \end{cases} $$

En posant: \(\pi = \begin{pmatrix} s_{1}, & ..., & s_{i}, & ..., & s_{n} \end{pmatrix}\)

Matrices de transitions singulières

Nous ferons quand même remarquer que la situation peut nécessiter quelques éclaircissements. Il est, en effet, possible d'avoir des matrices de transitions qui sont singulières, où les valeurs propres seront dégénérées.

$$ C = \begin{pmatrix} 0.5 & 0.5 \\ 0.5 & 0.5 \\ \end{pmatrix} $$

On peut alors se demander ce qu'il va advenir des solutions au système précédemment mentionné. Intuitivement, ces matrices auront quand même un état stationnaire, puisqu'il semble logique de penser qu'on passera autant de temps sur chacun des états dans un tel système. Heureusement pour nous, il existe le théorème de Perron–Frobenius qui affirme qu'il existera au moins une valeur propre réelle avec un vecteur propre strictement positif.

---

Maintenant que nous sommes revenus sur la notion des chaînes de Markov, vous aurez peut-être observé quelque chose. Dans la définition du problème initial du calcul des sanctions, on retrouve deux caractéristiques principales:

• Le problème concerne des graphes.
• Il s'exprime en termes de pourcentages; au début, chaque entité possède 100% d'elle-même et des parts sont vendues à différents actionnaires. Néanmoins, la somme des pourcentages de détention directs est toujours égale à 100% (s'il manque des pourcentages, on considérera qu'ils sont encore détenus par la société).

Ce qui correspond (comme par le plus grand des hasards) à la définition d'une chaîne de Markov !

Deuxièmement, en quoi consiste pratiquement le problème ?

• Déterminer quelles sont les filiales d'une entité sanctionnée.
• Quel est le pourcentage de détention associée à cette filiale.

Ces deux points sont associés à un autre problème classique en informatique. La notion d'accessibilité (reachability) sur une chaîne de Markov se retrouve dans des problèmes de preuves formelles de programmation et, entre autres, dans le concept de model checking¹ sur de la Probabilistic Computation Tree Logic ou PCTL².

Algorithmes de recherche de cycles et résolutions des chaînes

Après ce rappel sur les chaînes de Markov, n'oublions pas que le problème consiste d'abord à déterminer quelles sont toutes les filiales de notre entité sanctionnée et quel est le pourcentage de détention associé.

Le plan d'attaque du problème devrait être un peu plus clair et mieux se dessiner. Il consiste à:

• Trouver toutes les chaînes de Markov.
• Calculer les pourcentages agrégés en amont et en aval de ces chaînes, lorsqu'il n'y a tout simplement pas de cycles.
• Calculer les états stationnaires de ces chaînes si elles sont initiales (au niveau de l'entité sanctionnée - en faisant l'hypothèse que seules les entités filiales peuvent être sanctionnées, même si une entité sanctionnée est détenue entièrement par une société, son actionnaire ne sera pas concerné par la sanction).
• Appliquer la correction adéquate à la limite avec une chaîne de Markov irréductible.
• Traiter de manière adéquate les chaînes réductibles présentes sur le chemin ou terminales (au niveau des filiales les plus basses).

Trouver les chaînes de Markov

La première étape consiste donc à trouver toutes les chaînes de Markov présente dans les données. Or, nous cherchons toutes les chaînes irréductibles, c'est-à-dire où il est possible d'accéder à chacun des nœuds depuis n'importe quel nœud originel en employant les transitions existantes.

Cette définition correspond exactement à la notion des composantes fortement connexes (strongly connected components) sur un graphe dirigé (Direct graph). Ce problème¹ était déjà énoncé dans les années 60. Mais il existe classiquement 3 algorithmes pour résoudre ce problème:

Kosaraju-Sharir

Un algorithme a été proposé indépendamment par deux informaticiens, Sambasiva Rao Kosaraju² et Micha Sharir³. Celui-ci est apparu vers la fin des années 80⁴, plus tardivement que celui proposé par Tarjan (que nous verrons juste après). Il a l'avantage d'être relativement simple à comprendre et d'être linéaire \(\Theta(|V| + |E|)\) avec un espace en \(\Theta(|V|)\).

def kosaraju_sharir_strongly_connected_components(G): visited = set() node_order = stack() # First pass for node in G: if node not in visited: visit_outgoing(node, visited, node_order) visited.clear() # Second pass strongly_connected_components = [] while len(node_order) != 0: node = node_order.pop() if node not in visited: strongly_connected_components.append([node]) visit(node, visited, strongly_connected_components) return strongly_connected_components def visit_outgoing(node, visited, node_order): visited.add(node) for v in node.outgoing_edges(): if v not in visited: visit(v, visited, node_order) node_order.push(node) def visit_ingoing(node, visited, strongly_connected_components): visited.add(node) for v in node.ingoing_edges(): if v not in visited: strongly_connected_components[-1].append(v) visit_ingoing(v, visited, strongly_connected_components)

L'algorithme se décompose en deux passes:

1. La première passe consiste à créer un ordre dans lequel les nœuds ont été parcourus. Il s'agit d'un simple parcours en profondeur (Depth First Search - DFS) qu'on applique sur chaque composante du graphe.
2. La seconde consiste à appliquer de nouveau un DFS, mais cette fois-ci sur le graphe avec les arêtes dans le sens opposé. À chaque fois qu'on visite un nœud pas encore visité, on lui associe une nouvelle composante fortement connexe qui est complétée par tous les nœuds pouvant être atteints par un DFS depuis ce nœud.

La propriété qui rend cet algorithme correct est le suivant. Chaque composante fortement connexe est reliée (ou non) aux autres par un ensemble d'arêtes allant toutes dans la même direction. Il n'est pas possible de revenir à une même composante fortement connexe depuis une autre éventuellement atteinte depuis celle-ci, cela impliquerait que la composante fortement connexe n'est pas maximale.

Comme en explorant les arêtes dans un sens, on va explorer toutes les composantes fortement connexes ainsi que celles qui peuvent être atteintes depuis celles-ci. Or, lorsqu'on traitera les arêtes dans l'autre sens, on va se retrouver à explorer tous les nœuds qui composent cette composante puisque les autres auront déjà été visités grâce à l'ordre du parcours qui aura été imposé.

Tarjan

L'algorithme de Robert Tarjan⁵ est un peu plus vieux 1972 et historiquement le premier algorithme en complexité linéaire \(\Theta(|V| + |E|)\) avec un espace en \(\Theta(|V|)\) mais il se veut plus "efficace" que celui de Kosaraju-Sharir puisqu'il n'a besoin de ne parcourir qu'une seule fois le graphe à défaut de consommer un peu plus d'espace.

def tarjan_strongly_connected_components(G): visited = set() explored = stack() strongly_connected_components = [] index = 0 for node in G: if node.index is None: index = visit(node, visited, explored, index, strongly_connected_components) return strongly_connected_components def visit(node, visited, explored, index): node.index = index node.low_link = index index += 1 explored.push(node) node.on_stack = True for v in node.outgoing_edges(): if v.index is None: index = visit(node, visited, explored, index, strongly_connected_components) node.low_link = min(v.low_link, w.low_link) elif v.on_stack: node.low_link = min(v.low_link, w.index) if v.low_link = v.index: strongly_connected_components.append([]) do: w = explored.pop() w.on_stack = False strongly_connected_components[-1].append(w) while w != v;

L'algorithme se base sur la propriété de low link qui correspond à l'identifiant du nœud le plus petit qu'on peut atteindre depuis un nœud. Seulement, lors d'un parcours, l'id minimal que l'on peut atteindre peut changer en fonction du parcours que l'on effectue.

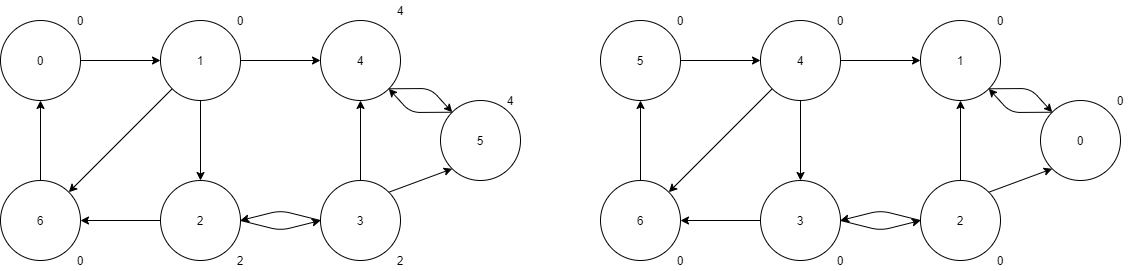
Afin de répondre à cette problématique, un ensemble de nœuds considérés comme "valides" est tenu à jour dans explored et où l'on peut puiser la valeur de low_link sans crainte. Les nœuds sont ajoutés dès qu'ils sont explorés pour la première fois, et retirés à chaque fois que l'entièreté de la composante fortement connexe a été trouvée.

L'algorithme en lui-même consiste à effectuer un parcours en profondeur, où à chaque fois que l'on tombe sur un nouveau nœud, on lui assigne un id, une valeur de low link et on l'ajoute à la stack.

Lors du retour de l'appel au DFS, si le nœud précédent est sur le stack, alors on prend le minimum entre la valeur actuelle du low link et celle du dernier nœud (ce qui permet de propager la valeur du low link à travers le cycle).

Une fois qu'on a parcouru tous les enfants, si le nœud actuel a créé une composante (si son id correspond à low link), alors on extrait tous les nœuds du stack jusqu'à retomber sur le nœud actuel et former la composante fortement connexe associée.

Path-based strong component algorithm

Un autre algorithme assez populaire, et proposé (entre autres) par Dijkstra⁶ en 1976. Sa complexité est linéaire \(\Theta(|V| + |E|)\) avec un espace en \(\Theta(|V|)\) mais il se veut aussi "efficace" que celui de Tarjan puisqu'il parcourt également une seule fois le graphe et, selon les implémentations, peut employer moins d'espace que ce dernier.

def path_based_strongly_connected_components(G): unknown_nodes = stack() pending = stack() preorder = [0 for v in G] c = len(G.nodes()) strongly_connected_components = [] for node in G:/span> if preorder[node] == 0: visit(node, unknown_nodes, pending, preorder, c, strongly_connected_components) def visit(node, unknown_nodes, pending, preorder, c, strongly_connected_components): unknown_nodes.push(node) preorder[node] = unknown_nodes.top() pending.push(node) for v in node.outgoing_edges(): if preorder[v] == 0: c = visit(v, unknown_nodes, pending, preorder, c,strongly_connected_components) else: while B.top() > pending[v]: B.pop() if B.top() == pending[node]: B.pop() c += 1 strongly_connected_components.append([]) while unknown_nodes.top() >= pending[node]: w = unknown_nodes.pop() strongly_connected_components[-1].append(w) pending[w] = c

Cet algorithme est sans doute inspiré par l'un de ceux proposés pour répondre à la question du tri topologique. Il emploie deux stacks, l'un pour retenir les sommets qui font partie de la composante courante et qui n'ont pas encore été assignés, et l'autre pour le chemin actuellement étudié où il n'y a pas encore d'indice sur le fait qu'ils appartiennent à des composantes différentes. On peut voir le stack pending comme l'équivalent du concept de low link de Tarjan.

Calcul des pourcentages agrégés en l'absence de cycles

Il s'agit sans doute de l'algorithme le plus simple lié à ce problème. Il consiste simplement à additionner tous les pourcentages, de détention d'une entité, pondérés par le chemin d'actionnariat considéré. On préférera sans doute employer une technique relative aux tris topologiques si l'on s'intéresse à toutes les sources, ou à un simple parcours en largeur si l'objectif ne se concentre que sur une seule source.

États stationnaires et chaînes irréductibles

Nous l'avons vu, chercher les états stationnaires d'un système correspond en réalité à répondre aux conditions:

$$ \pi * A = \pi \\ \Vert \pi \Vert = 1 $$

Il existe deux grandes manières de résoudre ce problème, trouver le bon vecteur propre qui satisfait ces équations:

1. La manière la plus classique consiste à appliquer une décomposition QR en exploitant le procédé de Gram-Schmidt. En cherchant à résoudre: \(\pi * (A − Id) = 0\)
2. En pratique, la matrice de transition est essentiellement creuse et l'on ne cherche qu'un seul vecteur propre ayant la plus haute valeur propre (\(1\)). On peut alors chercher du côté du concept de la périodicité des chaînes de Markov et itérer la multiplication de matrices jusqu'à obtenir un résultat satisfaisant. Ces méthodes sont dites de power series et l'un des algorithmes, qui nous intéresse spécifiquement pour les matrices de transition d'une chaîne de Markov, est l'itération d'Arnoldi⁸.

Des questions plus philosophiques doivent se poser quant au choix de l'algorithme en fonction de la taille du problème considéré, de la stabilité numérique et du temps que l'on souhaite y accorder.

En pratique, on peut appliquer un algorithme similaire à celui-ci (ici en employant la librairie numpy⁷), en supposant qu'on note en colonne le pourcentage des "arêtes qui viennent" et en ligne, celles "qui partent" du nœud:

def get_steady_states(A): evals, evecs = np.linalg.eig(A.T) # Calcul les valeurs et vecteurs propres. evec1 = evecs[:, np.isclose(evals, 1)] # Vecteurs propres dont la valeur propre est proche de 1. # np.isclose va produire un array où l'on ne veut que la première valeur, # qui est censé être la plus grande valeur propre 1. evec1 = evec1[:, 0] # On normalise et retourne uniquement la partie réelle. stationary = evec1 / evec1.sum() return stationary.real

Par exemple, si l'on prend la matrice suivante:

$$ A = \begin{pmatrix} 1 - p & p \\ 1 - p & p \\ \end{pmatrix} $$

On obtient bien pour états stationnaires \(\begin{pmatrix} 1 - p & p \end{pmatrix}\), ce qui semble assez naturel puisqu'à chaque instant, on a \(p\)% de chance de rester ou d'aller dans l'état \(p\).

Chaînes de Markov réductibles

Cette partie est un peu "technique", en ce sens qu'il faut veiller à bien faire attention. Peut-être que certains se demanderont pourquoi on ne peut pas calculer l'état stationnaire directement sur tout le graphe. Prenons pour exemple, le graphe suivant:

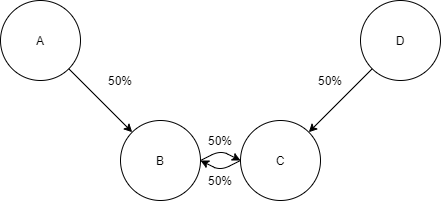
On peut lui associer la matrice suivante:

$$ A = \begin{pmatrix} 1.0 & 0.5 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.5 & 0.0 \\ 0.0 & 0.5 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.5 & 1.0 \\ \end{pmatrix} $$

On s'attendrait nativement que les nœuds \(A\) et \(D\) se partagent la moitié de l'actionnariat du cycle. Malheureusement, nous obtenons ceci comme valeurs propres:

$$\begin{pmatrix} 0.5 & -0.5 & 1.0 & 1.0 \end{pmatrix}$$

et ceci comme vecteurs propres:

$$\begin{pmatrix} 0.00 & 0.00 & 0.80 & 0.00 \\ 0.71 & 0.71 & 0.53 & 0.27 \\ 0.71 & -0.71 & 0.27 & 0.53 \\ 0.00 & 0.00 & 0.00 & 0.80 \\ \end{pmatrix}$$

Nous observons que nous nous retrouvons avec deux valeurs propres valant \(1\) et ayant un vecteur propre similaire. Cela ne va pas, on ne peut pas appliquer simplement le calcul des états stationnaires dans cette situation.

États absorbants et systèmes d'équations

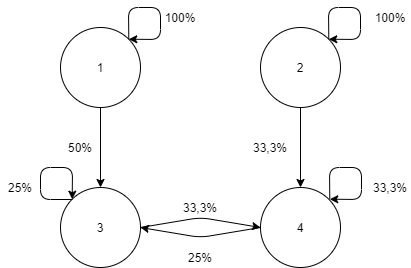
Quelles sont nos intuitions pour ce graphe ? Est-ce que le nœud 1 possède plus d'actionnariat que le nœud 2 ? Comment pondérer ces relations pour avoir quelque chose de cohérent ?

On peut définir le système d'équations:

$$ a_{ij} = p_{ij} + \sum_{k \in \text{transient}} p_{ik} a_{kj} $$

Où \(a_{ij}\) représente la probabilité asymptotique de passer de l'état \(i\) à l'état \(j\), \(p_{ij}\) la probabilité de transition entre les deux états et transient représente un état qui fait partie de la composante fortement connexe et \(j\) représente un état absorbant du système.

On se retrouve avec les quatre équations:

$$ \begin{cases} a_{31} = p_{31} + p_{33} a_{31} + p_{34} a_{41} \\ a_{41} = p_{41} + p_{43} a_{31} + p_{44} a_{41} \\ \end{cases} $$

et:

$$ \begin{cases} a_{32} = p_{32} + p_{33} a_{32} + p_{34} a_{42} \\ a_{42} = p_{42} + p_{43} a_{32} + p_{44} a_{42} \end{cases} $$

Si l'on remplace par les valeurs de \(p_{ij}\) et cherchons à trouver les valeurs de \(a_{31}\) et \(a_{41}\), on obtient:

$$ \begin{cases} a_{31} = 1/2 + 1/4 a_{31} + 1/4 a_{41} \\ a_{41} = 0 + 1/3 a_{31} + 1/3 a_{41} \\ \end{cases} \iff \begin{cases} a_{31} = 4/5 \\ a_{41} = 2/5 \\ \end{cases} $$

et:

$$ \begin{cases} a_{32} = 1/5 \\ a_{42} = 3/5 \\ \end{cases} $$

Vous pouvez observer plusieurs propriétés sur ces résultats:

• La probabilité d'aller de l'état 3 à l'état 1 est plus élevée que celle d'aller de 4 vers 1. De même, 4 vers 2 est plus élevé que 4 vers 1. Cela nous rassure sur le sentiment de proximité des nœuds.
• La somme des \(a_{31}\) et \(a_{41}\) ne donne pas 1 comme le système est ouvert.
• La somme des \(a_{31}\) et \(a_{32}\) est bien égale à 1. Ce qui nous rassure beaucoup.

États absorbants et équations matricielles

Même si la représentation algébrique du problème est assez intuitive, on préfère davantage travailler avec une représentation matricielle en informatique.

$$ A = \begin{pmatrix} 1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.5 & 0.0 & 0.25 & 0.25 \\ 0.0 & 0.33 & 0.33 & 0.33 \\ \end{pmatrix} $$

On observe que la matrice peut se décomposer en 3 parties:

$$ A = \begin{pmatrix} I & 0 \\ R & Q \\ \end{pmatrix} $$

Avec \(I\) la matrice identité, \(R\) la matrice de transitions des états transients vers les états absorbants et \(Q\) la matrice contenant uniquement les états transients.

Le système d'équations précédemment mentionné consiste, en réalité, à calculer le résultat de: \(A = R + QA\). Pour cela, il suffit d'isoler \(A\) et on aura: \(A = (I - Q)^{-1} R\). On a également la chance d'avoir que \((I - Q)\) est inversible puisque, physiquement, il doit exister une solution au problème.

Ce qui est absolument génial, c'est qu'on peut répondre à deux autres questions sous cette forme:

Quel est le nombre d'états en moyenne que l'on va parcourir avant d'arriver dans un état absorbant ? Où plus précisément, étant donné un état \(i\), combien de fois allons-nous visiter l'état \(j\) en moyenne et noté \(e_{ij}\) ? Pour cela, il suffit de calculer:

$$ \begin{cases} e_{ij} = \sum_{k \in \text{transient}} p_{ik} e_{kj} & \text{if } i != j\\ e_{ii} = 1 + \sum_{k \in \text{transient}} p_{ik} e_{ki} & \text{otherwise} \end{cases} $$

Mais il se fait que \(E\) correspond exactement à la définition de \((I - Q)^{-1}\) !

Ce qui correspond, dans notre cas, à :

$$ E = \begin{pmatrix} 1.595 & 0.786 \\ 0.595 & 1.786 \\ \end{pmatrix} $$

Et si on additionne les éléments de la première colonne, nous avons \(\approx 1.6 + 0.6 \approx 2.2\), en moyenne, on va transiter par 2.2 états avant d'arriver sur un état absorbant.

La question opposée. Combien de transitions vont être prises avant d'arriver à un état absorbant ?

C'est un petit peu plus complexe, mais il faut calculer le temps moyen de passage (conditionnel) de l'état i vers j, cela revient à résoudre le système d'équations:

$$ a_{ij} m_{ij} = a_{ij} + \sum_{k \in \text{transient}} p_{ik} a_{kj} m_{kj} $$ $$ \begin{cases} a_{32} m_{32} = a_{32} + p_{33} a_{32} m_{32} + p_{34} a_{42} m_{42} \\ a_{42} m_{42} = a_{42} + p_{43} a_{42} m_{42} + p_{44} a_{42} m_{42} \\ \end{cases} $$ $$ \begin{cases} 1/5 m_{32} = 1/5 + 1/4 * 1/5 m_{32} + 1/4 * 3/5 m_{42} \\ 3/5 m_{42} = 3/5 + 1/3 * 1/5 m_{42} + 1/3 * 3/5 m_{42} \\ \end{cases} = \begin{cases} m_{32} = 17/5 \\ m_{42} = 31/5 \\ \end{cases} $$

Conclusions

Dans cette partie, nous sommes revenus sur différents algorithmes permettant d'identifier les composantes fortement connexes dans un graphe. Malgré l'apparente simplicité du problème, plusieurs solutions existent et proposent des compromis différents que ce soit dans leur complexité, l'espace mémoire additionnel requis ou de motifs d'accès et de parallélisme. Ensuite, une fois que nous avons identifié tous ces cycles, nous avons longuement discuté de la manière mathématiquement correcte de résoudre des chaînes de Markov réductibles et irréductibles, que ce soit par le biais de système d'équations ou une représentation plus "matricielle" du problème, avec exemple à l'appui.

Ingénierie et bricolage

Maintenant qu'on possède tou(te)s les composant(e)s pour résoudre le problème. Il ne reste plus qu'à les combiner pour finalement arriver au résultat attendu. Évidemment, tout n'est pas toujours aussi simple …

Données pourries

L'actionnariat des sociétés relève du domaine privé pour l'immense majorité des entreprises, et il n'est pas non plus concevable de chercher à vouloir déterminer ce qu'un individu possède. L'habitude est que les pays possèdent la liste des sociétés enregistrées sur leur territoire ainsi que des informations sur leur consolidation (afin de déterminer comment les revenus doivent être imposés). Si la société mère n'est pas située dans le même pays, il faut espérer pouvoir la retrouver dans celui mentionné (en espérant que les informations soient correctement encodées et sincères). De plus, certains pays ne veulent pas jouer le jeu, en ne communiquant volontairement pas l'information qu'ils possèdent.

Il existe néanmoins des systèmes internationaux de communication, qui sont connus sous les doux noms: échange automatique de renseignements (AEOI) comme le CRS (Common Reporting Standard) au niveau de l'OCDE et des accords internationaux (comme le MCAA - Multilateral Competent Authority Agreement), FATCA (Foreign Account Tax Compliance Act) pour les États-Unis; et ce, au travers d'outils qualifiés de CbC (Country-by-country reporting).

Cependant, ces conventions sont loin d'êtres parfaites, vues qu'implémenter de manière plus que "lacunaire" par certains pays, si ce n'est tout simplement non ratifiées par certains états. Il s'agit également d'accords internationaux, et rien n'empêche certains pays de ne pas jouer le jeu, en ne favorisant qu'un sens de l'accord par exemple (on pensera à un certain leader mondial en particulier avec sa population de 330 millions d'habitants). Néanmoins, il s'agit d'une première avancée majeure dans la lutte contre le blanchiment d'argent et l'évasion fiscale.

Outre des informations qui ne sont tout simplement pas disponibles, elles peuvent également être erronées ou incohérentes. Une typographie à l'introduction dans un système d'encodage, une ligne introduite à la place d'une autre, une erreur dans la reconnaissance optique de caractères, … Ne parlons même pas de la difficulté que peut représenter la situation de multinationales établies dans 150 pays et ayant créé et supprimé une vingtaine de sociétés dans la même année, alors que les années fiscales diffèrent d'un pays à l'autre. Quid de la situation lors de rachat, toutes les sociétés appartenant à un groupe financier ne sont pas forcément reprises par l'acquéreur et peuvent être abandonnées ou fusionnées dans tous les sens ?

Bref, on se retrouve avec de l'information incomplète et potentiellement erronée. De plus, un intermédiaire peut être le détenteur légal d'actions pour un tiers. On parle de plus en plus, au niveau européen, de bénéficiaires ultimes (ubo - ultimate beneficial owners) qui sont les individus réellement détenteurs de l'actionnariat d'une société et des dividendes de celles-ci. Il est généralement reconnu qu'il n'y a pas d'obligations d'être annoncés publiquement comme actionnaire si l'on possède moins de 5% de l'actionnariat (avec évidemment des exceptions en fonction de la structure de l'"actionnaire" - voir l'affaire Hwang en mars 2021)¹².

N'oublions pas le petit point bonus qui fait qu'une société ne possède pas toujours le même nom: 微软 (Wéiruǎn) signifie "Microsoft" en chinois ou encore: Proximus SA ou Proximus NV qui représente la même société dans deux des langues nationales belges. Pour ce qui est des individus, c'est le tonneau des danaïdes, avec toutes ses spécificités locales: William Henry Gates III plus connu sous le nom de "Bill" Gates, la féminisation des noms de famille comme en Grec ou en Russe, la notion même de nom plus qu'"éparses" dans certains pays, …

Problèmes de probabilités

Pour les diverses raisons que nous avons invoquées, et sans doute bien d'autres, on se retrouve avec de l'actionnariat qui ne vaut pas forcément 100%, qui est parfois supérieur ou inférieur à celui-ci. Il faut alors faire preuve d'imagination pour corriger les problèmes. Lorsqu'il manque, on peut considérer qu'il s'agit d'actionnariat qui demeure au sein de la société elle-même, ou alors on normalise tous les autres actionnaires afin d'arriver au pourcentage attendu. Dans le cas où l'actionnariat est supérieur à 100%, c'est plus embêtant et la renormalisation semble sans doute le plus adéquat lorsqu'une intervention manuelle n'est pas possible.

Il n'est pas rare non plus qu'une entreprise, en remettant ses comptes annuels (ses annual reports), s'occupe de mentionner l'actionnariat de ses filiales en spécifiant celles qu'elles possèdent directement et d'autres indirectement. Cette idée d'actionnariat indirect revient à dire que la chaîne de détention mènera éventuellement à cette fameuse entité avec le pourcentage indiqué. Il peut donc y avoir des inconsistances entre les pourcentages agrégés calculés sur base du pourcentage des détentions directes et de celui fourni par la société de manière indirecte. Dans ce cas, on choisira le pourcentage le plus élevé, mais qui respectera l'invariant de 100%. Ne parlons pas des concepts plus que "vagues" comme wholly owned, majority ou les fameux > x% derrière lesquels les pourcentages sont à interprétation du lecteur.

On peut également se demander ce qu'il adviendrait de l'usage des formules précédemment mentionnées lorsqu'elles sont employées sur des chaînes de Markov où la somme des pourcentages diffère de 100% … Assez naturellement, comme ces opérations consistent à chercher un état stationnaire, à calculer l'état à l'infini en prenant la matrice inverse, on risque de voir une absorption vers 0 si le pourcentage est inférieur à 1, et une explosion vers l'infini s'il est supérieur à 1.

Ceci soulève une autre question très intéressante. Quid de la stabilité numérique, du conditionnement ou de l'erreur, tout simplement. Il faut dire qu'on a beaucoup de chances pour ces problèmes puisqu'ils sont très largement étudiés et que notre problème spécifique se comporte "bien" sous ces conditions (les pourcentages sont rarement exprimés au-delà du pour cent milles - 0.001%).

Problèmes de taille

Mais, au fait, quelle est la taille du problème ? Combien existe-t-il d'entreprises dans le monde ou d'individus possédant de l'actionnariat dans au moins l'une d'entre-elles ? L'OCDE évoque un nombre de 350 millions d'entreprises³. Pour ce qu'il en est des individus, je ne pense pas que cette information soit trouvable, mais j'imagine un ordre de grandeur équivalent (sans doute inférieur, mais de l'ordre de plusieurs dizaines de millions). L'AMF fournit un nombre de 1,4 million d'individus en France ayant effectué des opérations boursières (qu'il faut sans doute pondérer par l'achat majoritaire de fonds et non d'actions à proprement parler). On se retrouverait avec une matrice de l'ordre de 400 millions x 400 millions, ce qui ne fait "que" \(1,6 \times 10^{17}\) entrées possibles, avec à chaque fois deux informations possibles: l'actionnariat direct et indirect. Soit, seulement, de l'ordre du demi-pétaoctet de données en théorie …

Évidemment, la situation est nettement meilleure en pratique parce que la matrice est extrêmement creuse. La majorité des sociétés n'ayant qu'un seul individu comme actionnaire. Seule une toute petite partie des sociétés possèdent plus de 10 actionnaires (essentiellement des sociétés cotées ou des crédits agricoles - au sens de groupements d'agriculteurs). Il y a également un phénomène très important qui intervient dans ce genre de situation et que l'on qualifie de rich club phenomenon, les sociétés ayant un actionnariat très important possèdent très souvent des détentions dans d'autres sociétés ayant un large actionnariat. Pensez aux fonds d'investissement qui se détiennent tous mutuellement. La taille de la composante fortement connexe maximale est d'ailleurs de l'ordre de la dizaine de millions de sociétés, impliquant pratiquement tous les pays, conglomérats, fonds d'investissement et capitalisations !

Vous l'aurez compris, le problème possède une taille non-négligeable, et il va falloir faire quelque peu attention lorsqu'on va écrire les algorithmes afin d'obtenir des temps raisonnables. Il faudra également exploiter au mieux le parallélisme, et les GPUs commencent à voir de plus en plus d'algorithmes adaptés à leur modèle de calcul spécifique⁴.

Identification des composantes fortement connexes

Malgré que l'algorithme de Tarjan soit asymptotiquement un algorithme optimal en temps linéaire, il est particulièrement difficile à paralléliser à cause de l'usage du parcours en profondeur qui est intrinsèquement séquentiel⁵.

Forward backward algorithm

De nombreux algorithmes se sont développés afin de résoudre ce problème, mais les plus efficaces se concentrent sur des variations⁸⁹ de l'algorithme dit de "FW-BW" (pour forward-backward)⁶. Malheureusement, en pratique, leurs performances ne sont pas transcendantes et n'arrivent à gagner que des petits facteurs multiplicatifs sur des cas réels (x5 avec 16 cœurs⁷).

L'algorithme FW-BW est basé sur le concept suivant:

On définit \(FW_{G}(i)\) (sur un graphe dirigé) l'ensemble des nœuds de \(G\) qui peuvent être atteints depuis le sommet \(i\); et \(BW_{G}(i)\) les nœuds depuis lesquels le sommet \(i\) est atteignable. De fait, \(FW_{G}(i) \cap BW_{G}(i)\) est la composante fortement connexe contenant le nœud \(i\). De plus, les nœuds restants peuvent être partitionnés en trois sous-graphes: ceux qui sont uniquement atteignables, ceux qui peuvent uniquement nous atteindre et ceux qui ne sont tout simplement pas connexes. Chacun de ces sous-ensembles est indépendant et peut être exécuté de manière récursive. Au final, la complexité peut être estimée en \(O(|E| \log |V|)\)¹⁴ !

Historiquement, comme cet algorithme peut mener à de nombreux sous-ensembles vides à devoir traiter, McLendon III et al.⁸ ont proposé l'étape de trim qui consiste à supprimer les nœuds qui n'ont que des arêtes entrantes ou sortantes, puisqu'ils ne peuvent faire partie d'un cycle.

def FW-BW-Trim(G, SCC): Trim(G, SCC) if len(G.nodes()) == 0: return v = G.nodes()[random()] FW = forward_reachable(G, v) # BFS ou DFS BW = backward_reachable(G, v) # BFS ou DFS S = FW & BW SCC = SCC | S in_parallel( FW-BW-Trim(FW ^ S, SCC), FW-BW-Trim(BW ^ S, SCC), FW-BW-Trim(G ^ (FW | BW), SCC) ) def Trim(G, SCC): do: for v in G.nodes(): if len(v.in()) == 0 or len(v.out()) == 0: SCC = SCC | set(set(v)) G = G ^ set(v) while G has not changed

Après, il y a de nombreux problèmes qui doivent être traités pour obtenir de meilleures performances dans des cas réels, comme: le fait de ne pas modifier directement le graphe, ne pas travailler avec des ensembles, mais plutôt des couleurs pour identifier les composantes fortement connexes, la gestion des petits cycles (taille 2) ou d'immenses (de l'ordre de \(|v|\))¹⁰. Le problème de parcours (d'accessibilité) est reporté sur celui de parallélisation d'algorithmes plus "classiques".

Online algorithm

Peut-être que la solution de vouloir traiter l'entièreté du graphe à chaque modification de ce dernier n'est peut-être pas la plus optimale. Il serait sans doute préférable de travailler de manière dynamique, en mettant à jour au fur et à mesure les informations dont on dispose.

Ce genre de questions était déjà apparu dans les années 70, avec le problème dit de: strong connectivity augmentation. La question est la suivante: "Quel est le nombre minimal d'arêtes qu'il faut rajouter pour former un cycle ?", problème qualifié de incremental. Dans l'article de Eswaran et Tarjan¹¹, il est montré que la complexité est linéaire sur un graphe non pondéré et est NP-Complet sur un graphe pondéré.

Pour la question inverse, "est-ce qu'on a toujours un cycle en supprimant une arête ?", qualifié de decremental, pendant de nombreuses années, l'algorithme proposé par Shiloach et Even¹²est resté l'état de l'art avec une complexité en \(O(|V|m)\) (amortie en \(O(|V|)\) - qu'il faut interpréter comme \(m\) modifications d'arêtes qui sont en moyenne en \(O(|V|)\))¹³.

Les algorithmes étant particulièrement complexes, je vous invite à lire les références suivantes: ^{15, 18, 19, 16, 17}. Mais autant si l'ajout de nouvelles arêtes est "simple", la suppression atteint un tout autre niveau. Le problème général d'addition et/ou de suppression est qualifié de fully dynamic.

L'idée principale que je voulais transmettre au travers de cette sous-partie est une réflexion plus globale sur une classe d'algorithmes qu'on qualifie de dynamique. En effet, quelle est la complexité d'un problème dans ce genre de cas ? Il est clair qu'une réponse du type "en \(O(1)\)" ne serait qu'une très grande approximation de la situation. En particulier, dans le domaine des: "Dynamic graph algorithms", on distingue 3 étapes principales:

• Le prétraitement (preprocessing time).
• Les opérations de requêtes (query time).
• Les mises à jour (update time).

Les deux dernières notions peuvent évidemment se combiner avec des concepts additionnels tels que la complexité pire, moyenne et surtout amortie; ou encore les notions de stratégies. Que deviennent alors les notions d'optimalité dans ces cas-là ?

Inversion de matrices

Problèmes

L'inversion de matrices est un problème beaucoup plus classique tant ces applications sont nombreuses. On retrouve déjà des traces dès 1967²⁰ en vue de paralléliser cette opération ! Seulement, on est davantage confronté à un problème de taille, où si la taille de la composante fortement connexe est trop grande, le problème risque de ne pas tenir en mémoire. Il faudra alors trouver une solution dite "out of core". Heureusement pour nous, certaines bonnes librairies peuvent répondre à cette problématique.

Online algorithm

On retrouve dès 1950²²les prémices d'une technique qui permet de mettre à jour la matrice inverse suite à l'ajout ou retrait d'une colonne ou encore d'une modification de la valeur d'une entrée. Il y a eu très peu de changements depuis le travail d'Hager en 1989²¹.

Solution alternative

En vue de réduire la taille de la matrice à inverser. Il peut être intéressant de réduire la taille de la composante fortement connexe en appliquant une logique de ce type: "Si le pourcentage agrégé du chemin est inférieur à \(10^{-5}\%\), alors on considère la détention de cette entité comme nulle". Cela permet d'éviter les contributions mineures qui n'auront pratiquement aucune conséquence sur les pourcentages de détentions "réels". De fait, cela supprime éventuellement tout un ensemble de liens et nœuds qui ne feront pas partie des composantes fortement connexes, ce qui permettra d'améliorer assez considérablement la complexité du problème en pratique.

Conclusions

Dans cet article, nous avons mentionné un besoin qui commence à apparaître dans de nombreuses juridictions à travers le monde. La problématique peut mener à une large variété d'interprétations légales (et dans une moindre mesure mathématique), ce qui peut avoir des conséquences financières importantes. Il m'a semblé important de communiquer que ce problème est connu depuis très longtemps en mathématiques et possède une solution claire. Seulement, l'interprétation des résultats de ces calculs est particulièrement déroutante et l'intuition fait souvent défaut.

Premièrement, nous avons abordé l'abstraction de ce problème dans un contexte plus mathématique. Les conséquences sur des cas classiques, ceux ayant des particularités au niveau de l'actionnariat ainsi que la différence de sémantique entre l'actionnariat, le contrôle et les revenus; enfin, les cas problématiques auxquels il faudra particulièrement faire attention.

Ensuite, nous avons vu le cadre qui sous-tend mathématiquement ce problème. Que ce soit par la définition des termes connexes ou l'interprétation intuitive de ces systèmes. Subséquemment, nous avons abordé les équations qui décrivent les chaînes de Markov et leurs solutions mathématiques, ou encore les questions additionnelles que l'on peut se poser relative à ces systèmes et leurs réponses.

Nous sommes alors revenus sur les algorithmes qui permettent de répondre à ces questions, en proposant un plan d'attaque plus globale à la problématique. Que ce soit par la détection des composantes fortement connexes, du calcul des états stationnaires des chaînes de Markov, le calcul des pourcentages agrégés ou la résolution de chaînes dites reducible.

Finalement, nous avons abordé d'autres problématiques qui pouvaient intervenir dans la résolution de ce problème. Nous avons cité l'absence de données au niveau mondial ou leur qualité inhérente (et sans doute utopique). Mais le point principal s'attardait sur la manière de gérer cette quantité astronomique de données que peut représenter le monde réel. Ce type de solutions étant généralement nettement plus avancées, même si souvent connues depuis de nombreuses années, est rarement vu dans le cadre académique standard et il nous a semblé bon de les présenter.

En conclusion, on espère que ce problème, somme toute assez classique, vous aura amené à vous poser des questions plus profondes sur la résolution d'un problème réel. Sur le cheminement mental que l'on peut effectuer si l'on reste suffisamment curieux et toujours à la recherche de nouveaux concepts et outils et sur les divers embarras que l'on peut rencontrer et auxquels il faut circonvenir.

Si vous souhaitez aller plus loin et voir qui sont les "grands gagnants du capitalisme" (ou plutôt "le": "BlackRock, inc."). Je ne peux que vous inviter à suivre les travaux de James B Glattfelder et de ses collègues Stefano Battiston et Stefania Vitali. M. Glattfelder a écrit de nombreux travaux à cet égard, et dans le prolongement de sa thèse de doctorat. Voici ses publications majeures à ce sujet, triées chronologiquement:

• GLATTFELDER, James B. et BATTISTON, Stefano. Backbone of complex networks of corporations: The flow of control. Physical Review E, 2009, vol. 80, no 3, p. 036104.
• VITALI, Stefania, GLATTFELDER, James B., et BATTISTON, Stefano. The network of global corporate control. PloS one, 2011, vol. 6, no 10, p. e25995.
• GLATTFELDER, James et BATTISTON, Stefano. The architecture of power: Patterns of disruption and stability in the global ownership network. Available at SSRN 3314648, 2019.