Introduction
Dans cet article, nous allons nous attarder sur quelques problèmes assez classiques en informatique mais qui possèdent un réel intérêt pour les utilisateurs finaux qui exploitent et traitent des données. Il s'agit des algorithmes de sélection (order statistics) ou de tri partiel. Ceux-ci permettent, par exemple, d'obtenir la liste des \(k\) meilleurs éléments ou d'offrir une certaine pagination dans les données. Malgré leur apparente simplicité, ils présentent quelques subtilités qui méritent que l'on s'attarde un peu dessus et qui sont à l'origine de questionnements plus profond sur la définition de complexité en informatique.
Cet article se veut purement théorique et nécessite quand même un petit bagage scientifique, il est préférable d'être à l'aise au niveau des concepts et connaissances de bases en informatique théorique (algorithmique et un peu de programmation) et cela s'adresserait donc à des étudiants étant plutôt vers la fin de leur bachelier (niveau licence pour nos amis français), début master.
Définition et statistique d'ordre
Les fonctions minimum ou maximum sont des fonctions qui apparaissent très régulièrement en informatique tant leurs applications sont nombreuses. À première vue, il est néanmoins plus rare de s'intéresser à la médiane, à des quantiles précis ou à d'autres valeurs plus arbitraires. Cependant, vous employez chaque jour un moteur de recherche qui vous donne les \(k\) meilleurs résultats pour une recherche donnée. Ou bien, vous désirez savoir quels sont les valeurs aberrantes dans les données que vous avez collectées. Ces questions sont d'autant plus critiques lorsqu'on fait de l'analyse de performance d'un programme, les temps d'exécution relevés suivent le plus souvent des distributions de type poisson ou bimodale et on peut s'intéresser aux temps des quantiles 99%, 99.9%, ... pour des questions de contrat et de qualité de prestation de services (SLA). On peut regrouper tous ces types de requêtes sous un nom commun: la statistique d'ordre (order statistics).
On peut définir le problème de manière plus générale comme suit:
Étant donné un ensemble \(A\) de \(n\) nombres (distincts) et un entier compris \(i\) entre 1 et \(n\), on cherche à déterminer l'élément \(x\) de \(A\) tel qu'il est plus grand que \(i-1\) éléments de \(A\).
Avec les cas particuliers tels que : le minimum correspond à \(i = 1\), le maximum coïncide avec \(i = n\) et la médiane coïncide avec \(i = n/2\).
Une solution évidente à ce type de problèmes consiste à trier la collection et à prendre l'élément à la position demandée. Seulement, on comprend bien qu'intuitivement, il y a un problème: trier est une opération en \(O(n \log n)\) mais chercher le minimum n'est qu'en \(O(n)\) (complexités exprimées en nombre de comparaisons). Mais où se cache donc cette complexité intermédiaire ?
Observons un autre problème, au lieu de chercher le maximum et puis le minimum, cherchons à la fois le maximum et le minimum d'un même tenant. Au lieu de comparer deux fois tous les éléments pour obtenir le maximum ou le minimum et donc avoir une complexité de \(2n\) comparaisons, on peut profiter du fait que si l'élément considéré est supérieur à celui actuellement maximum, il ne sert alors à rien de tester s'il est inférieur au minimum.
En pratique, au lieu de comparer chaque élément de l'ensemble avec l'élément minimal ou maximal courant, on compare d'abord chacune des paires de l'ensemble et puis seulement, on compare à l'élément minimal ou maximal actuel.
def find_min_or_max(A, inequality):
target_value = A[0]
for e in A[1:]: # Pour chaque élément de l'ensemble
if inequality(e, target_value): # S'il est plus grand ou plus petit
target_value = e # On modifie l'élément actuel
return target_value
def min_max(A):
min_a = find_min_or_max(A, min)
max_a = find_min_or_max(A, max)
return min_a, max_a
par rapport à:
def min_max(A):
min = A[0]
max = A[1]
if max < min:
min, max = max, min
for i in range(2, len(A), 2):
if A[i] < A[i + 1]:
if A[i] < min:
min = A[i]
if max < A[i + 1]
max = A[i + 1]
else:
if A[i + 1] < min:
min = A[i + 1]
if max < A[i]
max = A[i]
return min, max
On observe que dans la fonction min_max, on effectue au maximum \(3\) comparaisons par tour de boucle, mais on n'en effectue que \(n/2\). On obtient au final \(3n/2\) au lieu de \(2n\), ce qui est un gain non-négligeable de \(n/2\) pour quelque chose qui a l'air pourtant trivial ! Le gain peut sembler un peu dérisoire en pratique, mais l'opération de comparaison peut parfois être plus lourde, comme dans le cas de chaînes de caractères par exemple.
Pour l'exercice, on peut également se demander ce qu'il advient lorsqu'on cherche le second plus petit élément. L'astuce qu'on a employée sur le cas précédent ne fonctionne plus. En effet, la propriété employée ne tient pas. Par exemple, si la liste est déjà triée par ordre décroissant, on serait amené à effectuer \(4n\) comparaisons au final. Par contre, on peut appliquer une technique similaire à la recherche du minimum et revenir à \(2n\) comparaisons. Mais il est possible de faire mieux !
On peut organiser un tournoi, en comparant chacune des paires individuellement, à chaque tour, on garde l'élément le plus petit jusqu'à ce qu'il n'en reste plus qu'un. L'astuce est que, lors de ce tournoi, le plus petit élément a dû rencontrer le second plus petit élément. Et il suffit de chercher ce fameux second parmi tous les perdants ayant eu le plus petit élément comme opposant. On a donc pour complexité: \(n/2\) la première fois, puis \(n/4\), et ainsi de suite: \(n/2 + n/4 + .. + 1 = n - 1\) avec \(\log(n)\) tournois intermédiaires. Au final, la complexité peut être égale à \(O(n + \log(n))\).
Seulement, on commence à percevoir deux problèmes : - Premièrement, pour obtenir cette complexité, on est obligé de pouvoir déterminer quels étaient les opposants de l'élément vainqueur. Ce qui nécessite de l'espace mémoire supplémentaire par rapport aux cas précédemment mentionnés travaillant en espace constant. - Deuxièmement, les algorithmes proposés sont fondamentalement différents, et il semble difficile de pouvoir généraliser ces techniques pour le cas plus général.
Quickselect et équation récursive
Une solution élégante et générale au problème de sélection est basée sur l'algorithme du quicksort et dénommée quickselect1. En effet, celui-ci se base sur la propriété fondamentale que, sur base d'un élément pivot, tous les éléments plus petits que celui-ci seront du même côté et ceux plus grands, de l'autre. La position du pivot étant de facto le rang de celui-ci. Il ne restera plus qu'à prendre l'embranchement qui contiendra le rang souhaité jusqu'à aboutir à celui-ci.
def quickselect(A, i, j, rank):
"""
Fournis l'élément situé à la position *rank* du vecteur *A* "trié" entre les bornes *i* et *j*
"""
if i == j:
return A[i]
pivot = chose_pivot(A, i, j) # Stratégie de sélection du pivot
partition(A, i, j, pivot) # Partitionnement, tous les éléments entre i et pivot - 1
# seront plus petits que le pivot et pivot + 1 à j seront plus grands
k = pivot - i + 1
if rank == k: # Si le pivot correspond au rang
return A[pivot]
elif rank < k: # Si le rang est à gauche du pivot (un indice plus petit)
return selection(A, i, pivot - 1, rank)
else: # A droite
return selection(A, pivot + 1, j, rank - k)
La complexité d'une telle fonction est déterminée par deux critères:
- L'algorithme de partitionnement, qui sépare tous les éléments inférieurs au pivot de ceux supérieurs. Néanmoins, celui-ci peut facilement être implémenté en \(\Theta(j-i)=\Theta(n)\).
- Le choix du pivot et toutes ses conséquences en terme de récursion.
Commençons par le cas quasi-idéal, supposons que le pivot sélectionné à chaque fois corresponde pile-poil à l’élément médian (mais que le rang n’est pas un élément de cette suite). L'espace de travail sera alors divisé en 2 et, on va effectuer la récursion sur l'une des deux parties. La charge de travail aura donc l'aspect \(O(n) + O(n/2) + O(n/4) + ... = \Omega(n)\), soit linéaire et seulement avec un facteur 2 ! On fera remarquer que, contrairement au quicksort idéal, la charge de travail diminue à chaque étape, alors que dans le cas du tri, la charge de travail reste constante, on continue de partitionner \(O(n)\) éléments à chaque étape, sachant qu'il existe \(O(\log n)\) étapes, d'où le \(\Omega(n \log n)\).
D'autre part, le pire cas peut être beaucoup plus catastrophique. Il suffirait que le pivot choisi soit, à chaque étape, l'élément maximal ou minimal. Il n'y aurait donc, de fait, pas de partitionnement et la charge de travail ne diminuerait que de \(1\). On se retrouverait alors avec \(n\) étapes et une complexité en \(O(n^2)\). Ce qui est catastrophique en pratique.
Seulement, on peut se demander quelle est la probabilité de choisir le mauvais pivot à chaque étape ?
Dans ce pire cas, seuls \(2\) éléments sur les \(n\) sont totalement problématiques. À chaque étape, on effectue le même choix et ce, de manière indépendante, on se retrouve avec:
$$\prod_{i=2}^{n} \frac{2}{i} = \frac{2^{n-1}}{n!}$$
Si vous êtes comme moi, cette probabilité ne vous dit strictement rien, mais si on prend \(n = 20\), \(2^{n-1} = 5.2\mathrm{e}{5}\) et \(n! = 2.4\mathrm{e}{18}\), ce qui donne de l'ordre de \(10^{-13}\). Ce qui est extrêmement peu probable !
Cependant ce raisonnement est un peu fallacieux parce que si on avait pris le second pire élément, la situation n'aurait pas été franchement différente, ni même le troisième, etc... Il vaut mieux se poser la question de quelle probabilité peut-on espérer en moyenne ?
En tentant de majorer la complexité2, on peut considérer que l'élément que l'on cherche se retrouvera, à chaque fois, du côté de la partition ayant le plus d'éléments. On définit une variable aléatoire, indicatrice, \(X_{k}\) qui représentera le choix du pivot \(k\) et qui vaut \(1\) pour la valeur de \(k\) et \(0\) sinon. On se retrouve avec la récurrence suivante3:
$$T(n) \leq \sum_{k=1}^{n} X_{k} (T(max(k - 1, n - k)) + O(n)) = \sum_{k=1}^{n} X_{k} T(max(k - 1, n - k)) + O(n)$$
Où \(T(n)\) représente la quantité de travail associée à une instance du problème sur des données de taille \(n\). Cette complexité est bornée par la taille de la plus grande partition (fonction max) additionnié du coût du partitionnement (\(O(n)\) et qui ne dépend pas du pivot) et pondérée par le choix du pivot.
Mais comme on s'intéresse au cas moyen, on va chercher à calculer l'espérance de cette fonction de travail:
$$\begin{aligned} E[T(n)] & \leq E[\sum_{k=1}^{n} X_{k} T(max(k - 1, n - k)) + O(n)] \\ & = E[\sum_{k=1}^{n} X_{k} T(max(k - 1, n - k))] + O(n) \\ & = \sum_{k=1}^{n} E[X_{k}] E[T(max(k - 1, n - k))] + O(n) \\ & = \sum_{k=1}^{n} \frac{1}{n} E[T(max(k - 1, n - k))] + O(n) \\ \end{aligned}$$
Maintenant, on sait que la fonction max travaillera avec au moins \(n/2\) éléments.
$$E[T(n)] \leq \frac{1}{n} \sum_{k=n/2}^{n-1} E[T(n)] + O(n)$$
Et, supposons que, pour une taille suffisamment petite, la charge de travail soit essentiellement constante: \(\exists k, T(n \leq k) = O(1)\). Le tour de magie, pour résoudre cette équation récurrente, est de supposer que \(O(n)\) soit la solution de \(E[T(n)]\). Cela voudrait dire que:
$$\begin{aligned} E[T(n)] & \leq \frac{1}{n} \sum_{k=n/2}^{n-1} ck + an \\ & = \frac{c}{n} (\sum_{k=1}^{n-1} k - \sum_{k=1}^{n/2} k) + an \\ & = \frac{c}{n} (\frac{3n^2}{8} + \frac{n}{4} - 1) + an \\ & = c (\frac{3n}{8} + \frac{1}{4} - \frac{1}{n}) + an \\ & = cn - (\frac{5n}{8} - \frac{1}{4} + \frac{1}{n} - an) \\ & = cn - o(n) = O(n)\\ \end{aligned}$$
On en conclut que la complexité est en moyenne linéaire4.
Pour ce qui concerne la variance ou les autres moments, les techniques deviennent nettement plus poussées15 et dépassent très largement le contenu de cet article.
Nous ferons la remarque qu'il existe également un autre algorithme proposé par Floyd et Rivest6 pour résoudre ce problème et qui décompose le problème en 3 sous-parties au lieu de deux et qui présente une meilleure complexité théorique. En effet, il se base sur un échantillonnage des données afin de trouver le \(k\) élément en seulement \(1.5n + o(n)\) comparaisons avec une très grande probabilité alors qu'il est connu que n'importe quel algorithme déterministe devra effectuer au moins \(2n\) comparaisons dans le pire cas.
- C. A. R. Hoare. Algorithm 65: Find. Commun. ACM, 4(7): 321–322, July 1961. ISSN 0001-0782. doi: 10.1145/366622.366647
- KIRSCHENHOFER, Peter et PRODINGER, Helmut. Comparisons in Hoare's Find algorithm. Combinatorics Probability and Computing, 1998, vol. 7, no 1, p. 111-120.
- CORMEN, Thomas H., LEISERSON, Charles E., RIVEST, Ronald L., et al. Introduction to algorithms. MIT press, 2009.
- KNUTH, Donald E. Mathematical analysis of algorithms. STANFORD UNIV CALIF DEPT OF COMPUTER SCIENCE, 1971.
- PAULSEN, Volkert. The moments of FIND. Journal of Applied Probability, 1997, p. 1079-1082.
- FLOYD, Robert W. et RIVEST, Ronald L. Algorithm 489: The algorithm SELECT—For finding the i th smallest of n elements [m1]. Communications of the ACM, 1975, vol. 18, no 3, p. 173.
Quickselect et arbre de complexité
On peut également démontrer cette complexité d'une autre manière. En effet, on peut représenter la charge de travail sous la forme d'un arbre, où chaque décision, chaque nœud, peut avoir une plus ou moins grande complexité et où le nombre de sous-branches considérées importe.
Commençons par compter le nombre d'appels récursifs qui doivent être effectués au final. Au début, on a une collection de \(n\) éléments. À chaque appel récursif, on va supprimer (au moins) un élément de cette collection (le pivot) et recommencer sur la partie qui nous intéresse. Il y aura donc au plus \(n + 1\) = \(\Theta(n)\) appels récursifs, peu importe comment ceux-ci opèrent, pour aboutir aux feuilles terminales de taille 0. La preuve se fait par induction, étant donné que les entrées seront divisées en deux intervalles de \(k\) et \(n - k - 1\) éléments respectivement.
Maintenant, chaque décision de l'arbre, chaque partitionnement des données, peut s'effectuer en \(n - 1 = \Theta(n)\) comparaisons.
Il ne reste plus qu'à combiner ces deux éléments ensemble. Il existe deux techniques: - Soit on additionne toutes les tailles d'entrées associées à tous les appels récursifs. - Soit on compte le nombre de fois où sont comparés deux éléments du tableau entre eux.
La première approche semblant quelque peu difficile à calculer, on préférera la seconde approche qui présente une vue plus "verticale" que "horizontale" de l'arbre de travail.
On note \(a_{i}\) la valeur de \(A\) au rang \(i\) (en comptant les rangs à partir de 1). Et on note \(C_{ij}\) le nombre de fois que les valeurs \(a_{i}\) et \(a_{j}\) sont comparées. Le nombre total de comparaisons sera alors noté par la variable aléatoire suivante: $$X = \sum_{i=1}^{n}\sum_{j=i+1}^{n} C_{ij}$$
Ici, on s'intéresse à l'espérance: $$\begin{aligned} E[X] & \leq E[\sum_{i=1}^{n}\sum_{j=i+1}^{n} C_{ij}] \\ & = \sum_{i=1}^{n}\sum_{j=i+1}^{n} E[C_{ij}] \\ \end{aligned}$$
Mais comment évaluer cette partie \(C_{ij}\) ? Il faut observer que, si une paire est comparée, elle ne le sera plus par la suite. Ceci est lié au fait que les comparaisons n'opèrent que dans le cadre du partitionnement, où le pivot est comparé à tous les autres éléments une seule et unique fois, et aucune autre comparaison n'est effectuée par la suite entre ces éléments.
Donc pour avoir \(a_{i}\) et \(a_{j}\) comparés entre eux, il faut que: 1) l'un des deux soit le pivot. 2) ils soient dans le même sous-ensemble de la récursion.
On se retrouve avec le fait que, par définition: $$\begin{aligned} E[C_{ij}] & = 0 P(C_{ij} = 0) + 1 P(C_{ij} = 1) \\ & = P(C_{ij} = 1) \\ & = P(a_{i} et a_{j} soient comparés) \\ \end{aligned}$$
Ceci est beaucoup plus "simple" à calculer ! Nous l'avons dit, pour être comparés, les éléments doivent appartenir au même sous-ensemble et que l'un des deux éléments soit choisi pour pivot.
Commençons par le cas simple du quicksort. La probabilité correspond au problème du coupon collector problem, chacun des éléments a une chance d'être choisi parmi tout le sous-ensemble et les deux éléments sont indépendants, on a \(2 / (j-i + 1)\). $$\begin{aligned} E[X] & \sum_{i=1}^{n}\sum_{j=i+1}^{n} P(a_{i} et a_{j} soient comparés) \\ & = \sum_{i=1}^{n}\sum_{j=i+1}^{n} 2 / (j-i + 1) \\ & = \sum_{i=1}^{n}\sum_{k=1}^{n-i} 2 / (k + 1) \\ & \leq \sum_{i=1}^{n}\sum_{k=1}^{n} 2 / (k + 1) \\ & = 2n \sum_{k=1}^{n} 1 / (k + 1) \leq 2n \sum_{k=1}^{n} 1 / k \\ & = 2n H_{n} \\ & = 2n \Theta(\log{n}) \\ & = O(n \log{n}) \\ \end{aligned}$$ Avec \(H_{n}\), le \(n\)ième élément des nombres harmoniques (et qui est en \(\Theta(\log n)\)).
Or, dans le cas du quickselect, la position du rang intervient puisqu'on ne considère que le sous-ensemble qui le contient. Au lieu du facteur: \(2 / (j-i + 1)\), on se retrouve avec l'expression: $$\frac{2}{max(j-i + 1, j-k + 1, k-i + 1)}$$ C'est nettement plus gênant à analyser ... Une astuce bête et méchante consiste à diviser l'espace des possibilités en région. Ici, on prendra le cas que \(k < n/2\), l'autre étant symétrique.
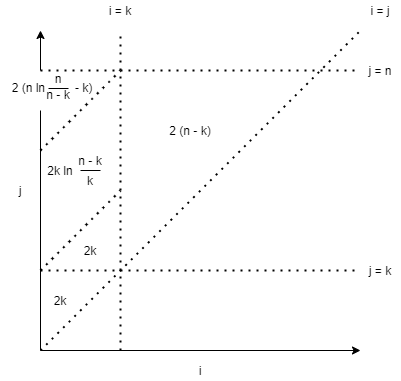
Comment interpréter ce diagramme ? Prenons, la région où \(i,j > k\), le plus grand triangle, borné par \(i=k, i=j\) et \(i=j\). À l'horizontal, les points sont de la forme: \(k + x\) où il y a donc \(x\) éléments à traiter, avec une probabilité de \(2/x\) et on a \(n-k\) "verticales", au final, on se retrouve avec \(2(n-k)\).
On peut additionner toutes les parties ensemble et obtenir une expression du type: $$(2n (1 + ln \frac{n}{n-k}) + 2k ln \frac{n-k}{k}(1 + o(1))$$
Expression qui est maximisée pour \(k = n/2\), on se retrouve au final avec: $$2n (1 + ln 2 + o(1)) \leq 4n + o(n) = O(n)$$
Médiane des médianes
Nous l'avons vu, la complexité moyenne de cet algorithme est en \(O(n)\) mais la situation peut vite dégénérer et mener à du \(O(n^2)\).
Il existe deux grandes familles de solutions pour répondre à ce genre de problème:
Stratégie hybride:
Une technique qui fonctionne particulièrement bien pour réduire la complexité de certains algorithmes consiste à changer la stratégie, à adapter l'algorithme en cours de route pour en employer un autre (on parle de adaptative algorithm). En l'occurrence, une stratégie communément admise pour répondre au problème du quickselect consiste à appliquer le même traitement qu'au quicksort (le fameux introsort1), opter pour un heapsort ou un insertion sort en fonction de si la récursion devient trop profonde ou que le nombre d'éléments considérés devient trop petit.
L'astuce étant que, même si ces autres algorithmes ont parfois des complexités supérieures (insertion sort est en \(O(n^2)\)), le fait qu'il soit appliqué sur peu d'éléments fait qu'ils sont rendus en temps "quasi"-constant ! L'autre bénéfice est que ces algorithmes peuvent avoir des performances en pratique bien supérieures à celles théoriques, en profitant d'optimisations matérielles ou grâce à des facteurs constants très petits pour la taille des données considérée2.
Meilleure stratégie:
La solution la plus évidente à notre problème consiste à améliorer la stratégie de sélection du pivot pour trouver celui qui se rapproche le plus de la médiane. Le problème est qu'on a un compromis à faire entre le travail qu'on peut s'autoriser à fournir pour trouver un meilleur pivot et améliorer la récursion, et le travail total de l'algorithme.
Le pas principal dans cette direction a été l'algorithme de la "médiane des médianes" ou BFPRT3 en l'honneur des auteurs (aussi célèbres que les avengers).
L'algorithme consiste à découper récursivement la collection en 5 sous-collections jusqu'à n'avoir que 5 éléments ou moins. On extrait alors l'élément médian de ces 5 éléments et on remonte la récursion en produisant la médiane des médianes des sous-collections traitées.
L'algorithme en lui-même est quelque peu complexe puisqu'il y a des récursions mutuelles et qu'on déplace en même temps les éléments dans la collection. Mais la complexité est "simple" à calculer.
Elle obéit à: $$T(n) \leq T(n/5) + T(7n/10) + O(n) = O(n)$$
La partie \(T(n/5)\) correspond au fait de trouver la "vraie" médiane des \(n/5\) médianes. Le terme \(O(n)\) apparaît lorsqu'on partitionne les données, sachant que tous les éléments auront été visités un nombre constant de fois afin de former les groupes de \(n/5\) éléments et pour prendre leur médiane. Finalement, le \(T(7n/10)\) s'explique par le fait que la moitié des sous-collections sont plus petites que la médiane des médianes (1/2 \* 1/5 = 1/10). Tout en bas de la récursion, dans les groupes de 5 éléments, au moins 3 éléments peuvent être, soit plus petits que le pivot, soit plus grands que celui-ci. Dans le pire cas, on n'exclut que \(3 * 1/10\) des éléments, on retombe alors sur le \(7n/10\).
La propriété magique étant que \(n/5 + 7n/10 < n\). Cela ne marcherait donc pas en prenant la médiane de 3 éléments.
Mais alors, pourquoi ne pas utiliser des plus petites sous-collections, diviser la charge en 7, 9 ou plus ? Pour exclure une plus grande partie des éléments et ne devoir appliquer la récursion que sur une sous-partie ? Le choix s'est porté sur le nombre 9 selon la technique du "Tukey's ninther"4 et qui sera choisi comme implémentation de la C library sous linux5. Les compromis entre les gains théoriques, les performances réelles et l'éventuel travail supplémentaire ont fait qu'il n'y a eu que peu d'évolutions depuis.
Par contre, dans le cadre général, le problème de la complexité nécessaire pour trouver l'élément médian a continué pendant quelques temps avec une complexité en \(\Omega((2 + \epsilon)n)\)6 et en \(O((2.95 + \epsilon)n)\)7.
Structure de données:
Toutefois, on peut aborder le problème d'une toute autre manière en utilisant une structure de données. Une solution assez évidente consiste à employer un heap dans le but de conserver les \(k\) meilleurs éléments, l'avantage de cette technique est que l'espace mémoire est assez contenu \(O(k)\) avec une complexité fixe en \(O(n \log k)\). Le gros désavantage étant que l'intérêt de cette méthode décroît au fur et à mesure que \(k\) tend vers \(n/2\).
Une solution, proposée par Knuth8 et en \(O(n - k + (k-1) \log (n-k+2))\), se base sur le tournoi que nous avions évoqué précédemment à propos de la recherche du second meilleur. L'idée étant que, dans le tournoi, les meilleurs éléments vont se retrouver proche du sommet, de la finale. Et il ne restera plus qu'à rejouer les parties en supprimant à chaque fois le nouveau vainqueur au sommet jusqu'à après avoir exclu tous les \(k-1\) premiers vainqueurs. Malgré une meilleure complexité en terme de comparaisons, cela nécessite néanmoins \(O(n)\) en espace.
Enfin, la solution sans doute la plus pérenne consiste à employer une des variantes possibles d'un Order statistic tree (par exemple un simple arbre binaire de recherche). On sait que chaque nœud possèdera \(B\) enfants qui diviseront l'ensemble des \(n\) sous-éléments (de la branche) en \(B\) parties de taille similaire, et ainsi de suite récursivement. On ne devra alors effectuer que \(O(\log_{B} N)\) opérations avec \(O(n)\) en mémoire. Solution qui a d'autant plus de sens vu l'optimalité théorique des B-tree pour de très nombreuses opérations.
- MUSSER, David R. Introspective sorting and selection algorithms. Software: Practice and Experience, 1997, vol. 27, no 8, p. 983-993.
- MARTÍNEZ, Conrado, PANARIO, Daniel, et VIOLA, Alfredo. Adaptive sampling strategies for quickselects. ACM Transactions on Algorithms (TALG), 2010, vol. 6, no 3, p. 1-45.
- BLUM, Manuel, FLOYD, Robert W.. , PRATT, Vaughan R.. , et al. Time bounds for selection. J. Comput. Syst. Sci., 1973, vol. 7, no 4, p. 448-461.
- TUKEY, John W. The ninther, a technique for low-effort robust (resistant) location in large samples. In : Contributions to Survey Sampling and Applied Statistics. Academic Press, 1978. p. 251-257.
- BENTLEY, Jon L. et MCILROY, M. Douglas. Engineering a sort function. Software: Practice and Experience, 1993, vol. 23, no 11, p. 1249-1265.
- DOR, Dorit et ZWICK, Uri. Median selection requires (2+/spl epsiv/) n comparisons. In : Proceedings of 37th Conference on Foundations of Computer Science. IEEE, 1996. p. 125-134.
- CARLSSON, Svante et SUNDSTRÖM, Mikael. Linear-time in-place selection in less than 3n comparisons. In : International Symposium on Algorithms and Computation. Springer, Berlin, Heidelberg, 1995. p. 244-253.
- KNUTH, Donald E. The Art of computer programming, Volume 3: Sorting and searching (1973). Google Scholar Google Scholar Digital Library Digital Library, 1998.
Përformance pratique
Nous avons abordé plusieurs aspects théoriques liés à cette problématique. Mais qu'en est-il en pratique ? Est-ce que les résultats théoriques confortent ceux obtenus en réalité ?
Nombre moyen de comparaisons par élément
Tout d'abord, nous avons mis en place une petite expérience afin d'avoir une estimation de la distribution du nombre moyen de comparaisons par élément en fonction du choix du \(k\). L'expérience consiste à:
- Prendre différentes valeurs de \(k\) (en tant que proportion de \(n\)).
- Compter le nombre de fois où l'élément \(i\) est comparé avec \(j\) (on incrémente de \(1\) à la fois l'élément \(i\) et \(j\) à chaque comparaison).
- Prendre la moyenne du nombre de comparaisons pour toutes les valeurs de \(i\).
On obtient alors un graphique de ce type:
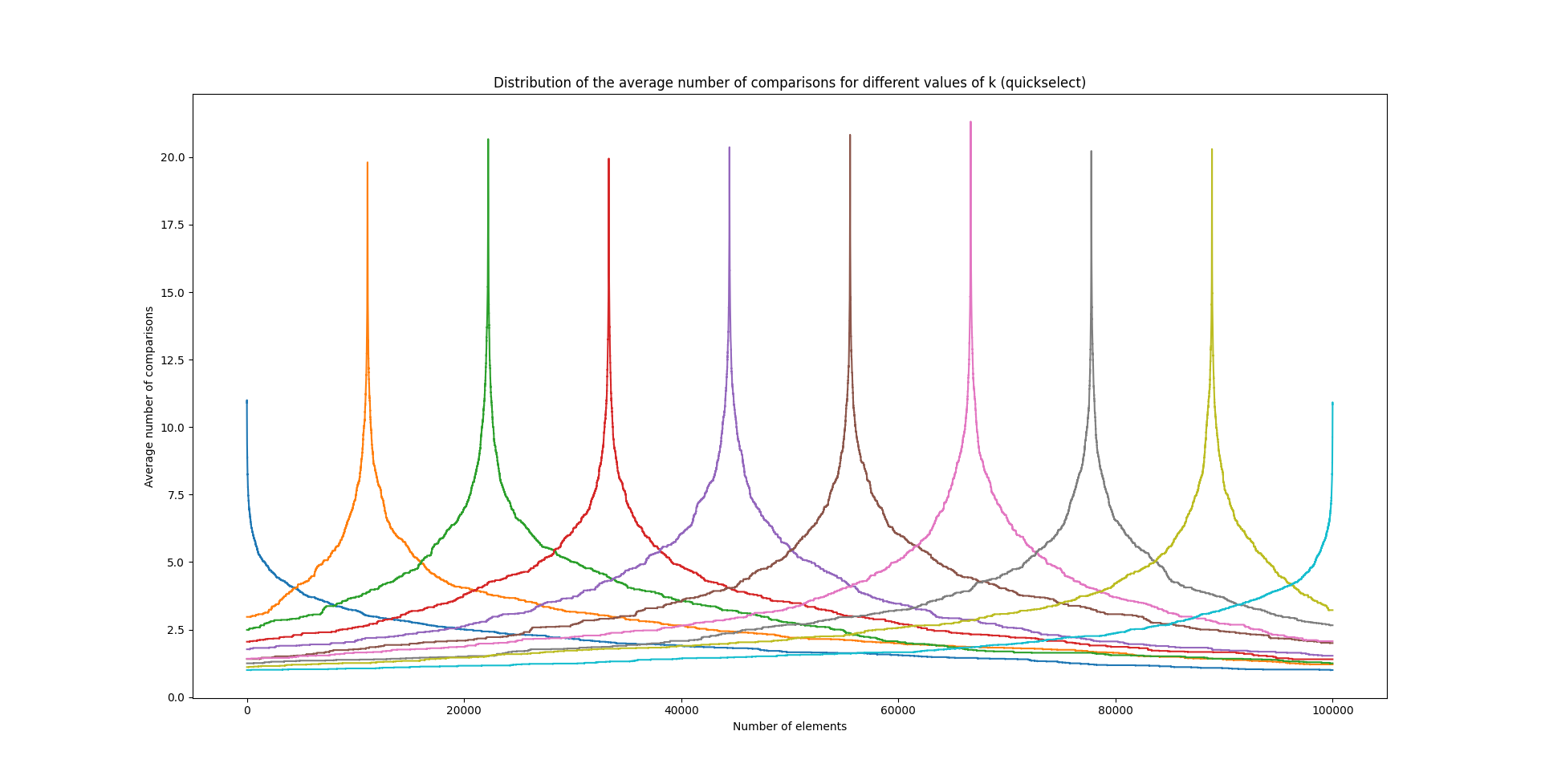
Qui représente la manière dont se distribue le nombre de comparaisons pour le choix d'un \(k\) en particulier (chaque pic et couleur correspondant à une valeur de \(k\) différente).
Premièrement, on se rend compte que les distributions obtenues sont très peu lisses malgré une moyenne effectuée sur 100 nombres de comparaisons. L'écart-type est particulièrement élevé (quasiment la moitié de la moyenne !). Deuxièmement, les courbes sont parfaitement symétriques autour de la cible, et leur forme générale fait sens puisqu'on aura d'autant plus tendance à comparer les éléments proches du rang et qu'une relation inversionnellement proportionnelle à la distance semble se justifier.
Nombre moyen de comparaisons total
Précédemment, en calculant le nombre moyen de comparaisons de quickselect, on était arrivé à la formule suivante:
$$(2n (1 + ln \frac{n}{n-k}) + 2k ln \frac{n-k}{k}(1 + o(1))$$On peut demander d'afficher le nombre moyen de comparaisons effectuées pour un \(k\) donné en comparaison à la formule théorique, et on obtient le graphique suivant:
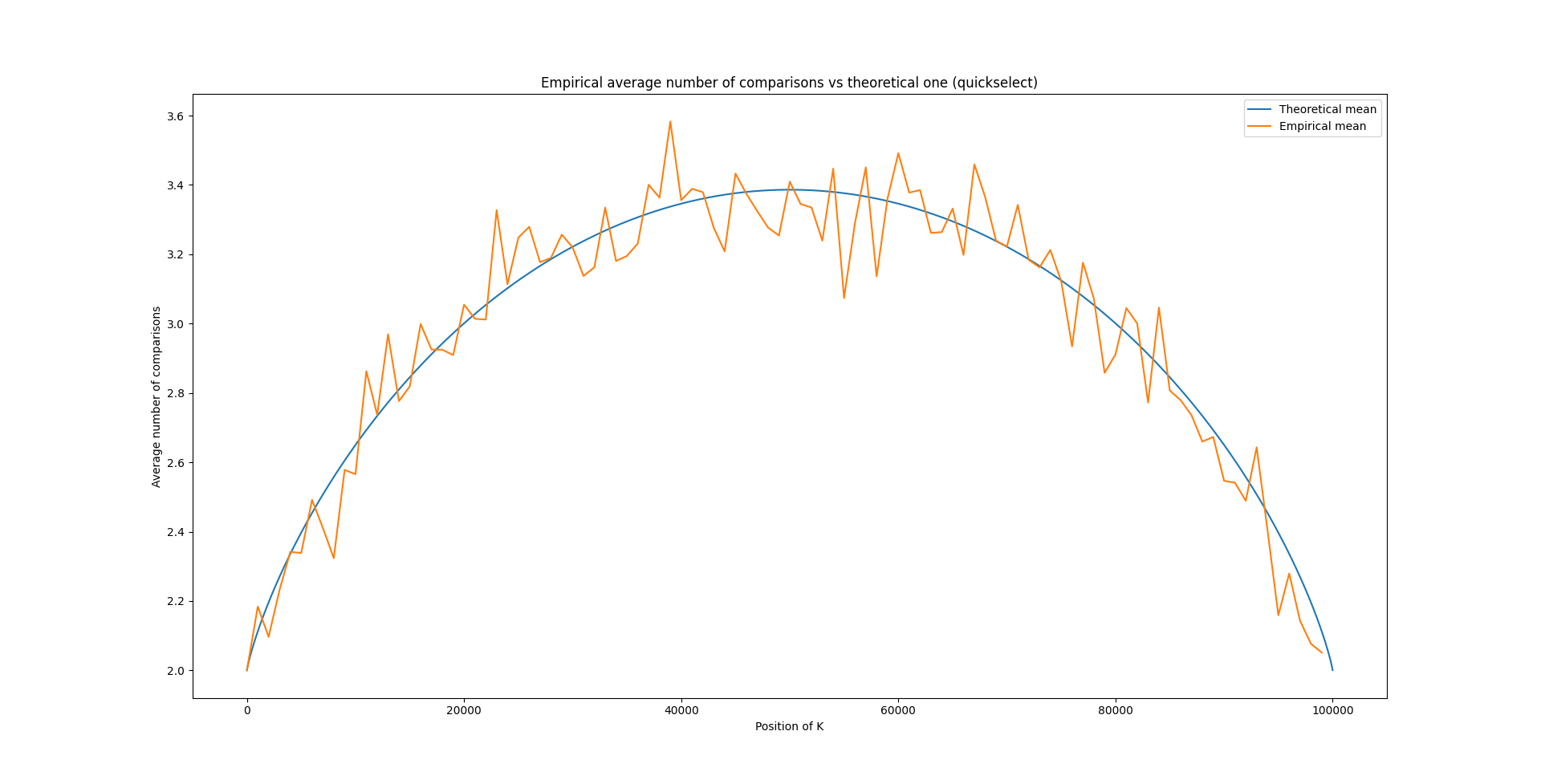
Il est impressionnant de voir à quel point la formule théorique est particulièrement proche du résultat empirique !
Median of medians et Tukey's ninther
On peut mener une expérience similaire avec les algorithmes du median of medians et Tukey's ninther:
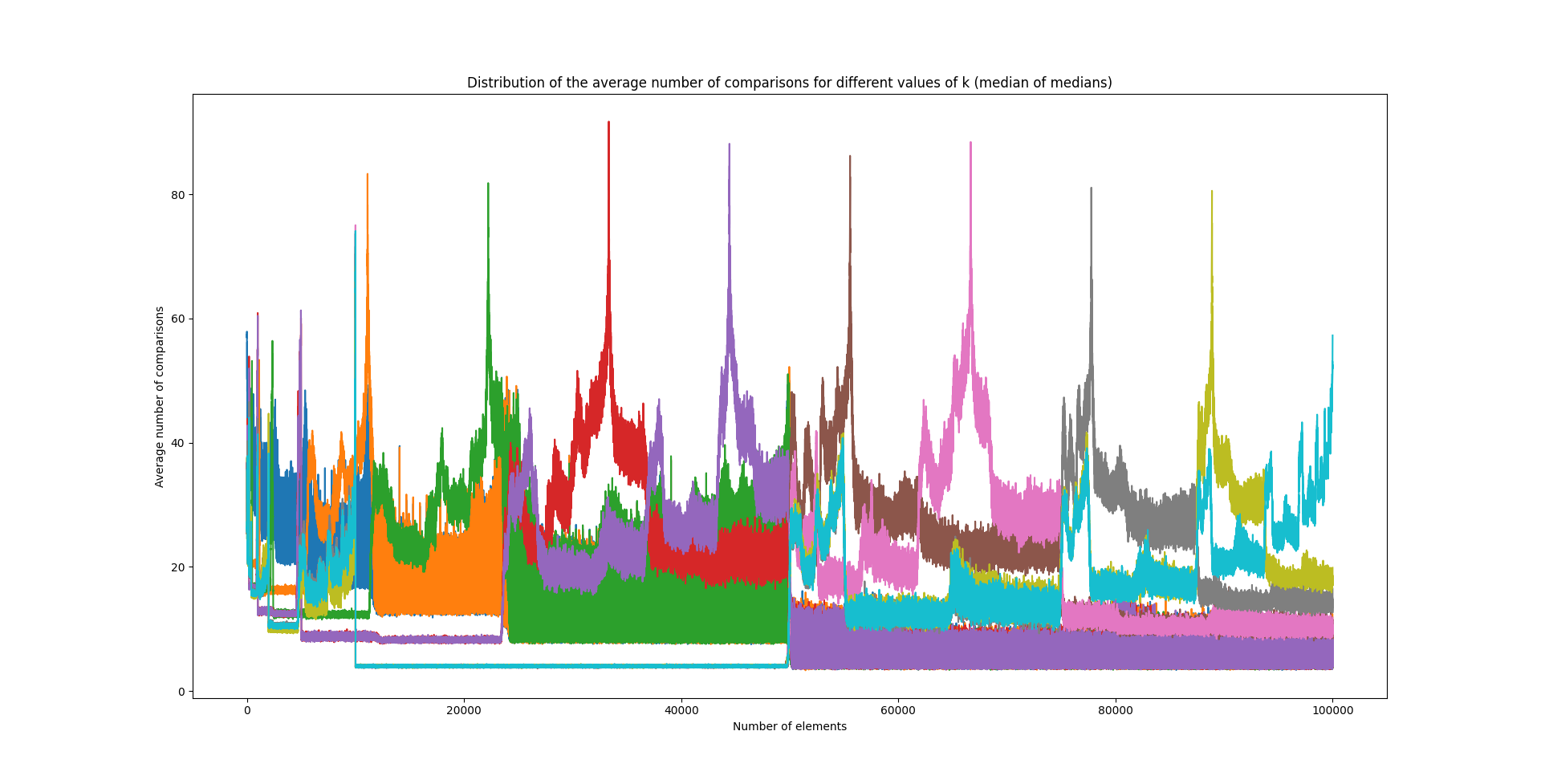
Pour l'algorithme de la médiane des médianes, cela devient nettement plus "abstrait" mais on observe un phénomène amusant ! Il semble y avoir des blocs de \(10000\) éléments et, surtout, que des régions sont complètement évincées par l'algorithme, que le nombre moyen de comparaisons chute drastiquement en sortant d'un de ces blocs.
Par curiosité, on peut rapidement se demander ce que donne Tukey's ninther:
Je ne commenterai que d'un seul mot: "code-barres".
Nombre moyen total de comparaisons
Finalement, on peut comparer le nombre moyen total de comparaisons pour chacun des algorithmes:
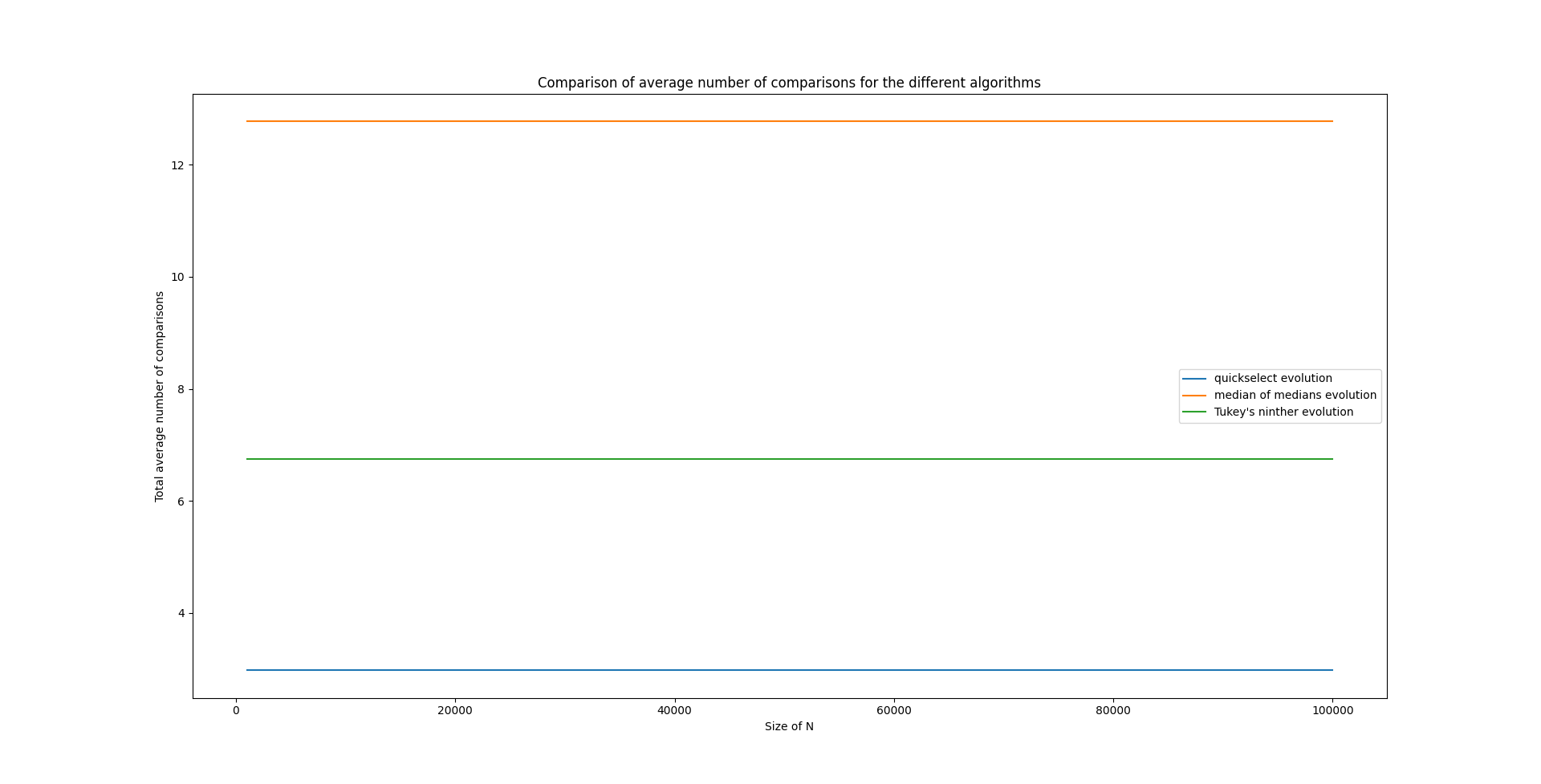
On voit que quickselect nécessite un peu plus de \(2\) fois moins de comparaisons que Tukey's ninther qui lui-même nécessite \(2\) fois moins de comparaisons que la méthode de median of medians. On remarque que le nombre moyen de comparaisons par éléments reste essentiellement stable pour le nombre d'éléments considérés, ce qui est en un sens assez logique, la complexité étant censée être linéaire avec la pente qui évolue peu.
Attention que tous les résultats obtenus ici ne concernent que le nombre de comparaisons et, non, les performances réelles de ces algorithmes en pratique. Si l'opération de comparaison est particulièrement coûteuse, alors l'algorithme du quickselect sera plus efficace, mais, peut-être qu'en pratique, c'est bien l'algorithme de Tukey's ninther qui est employé parce qu'il bénéficie davantage des optimisations matérielles ou qu'il offre des constantes plus petites pour les tailles de \(n\) qu'on traite habituellement. Indiquons également un intérêt pour le median of medians dans les cas d'external memory, en effet, celui-ci semble nécessiter de comparer le moins de blocs d'éléments ensemble. La complexité évaluée dans un tel modèle de calcul correspondant assez bien aux calculs de complexité probabiliste effectués ici (combien de fois le bloc \(i\) est comparé avec le bloc \(j\)).
Conclusions
Nous l'avons vu, malgré une apparente simplicité, ces problèmes présentent une réelle complexité sous-jacente. Leur étude peut s'avérer très pointue, si on s'intéresse tant aux aspects purement algorithmiques que ceux plus statistiques. Ce genre d'algorithme a fait partie d'un questionnement plus profond sur les notions de complexité: Que signifie le cas moyen, le pire ou le meilleur ? Est-ce que ces derniers existent pour chaque algorithme ? Peut-on définir une distribution de performance d'un algorithme, quelles sont les limites de ce concept ? Ce genre de questions verra émerger le champ de l'analyse probabiliste des algorithmes qui prodiguera un environnement vaste de réflexions et fera émerger de nombreux noms célèbres de l'informatique théorique.
La problématique de complexité minimale pour résoudre le problème change aussi radicalement avec ce nouveau paradigme. L'une des interprétations proposée par Yao (- Yao's principle - et sujet d'une conjecture encore ouverte) consiste à représenter le concept d'adversaire, dans ce cadre, comme une distribution de probabilité sur un ensemble d'algorithmes déterministes1. Dans le but de définir la borne inférieure sur des algorithmes aléatoires, il est suffisant de trouver une distribution appropriée qui représente les entrées et de prouver qu'un algorithme déterministe ne peut être meilleur par rapport à cette distribution.
Une question fortement liée à ce problème est le secretary problem. Le contexte est le suivant: "on cherche à recruter le meilleur candidat parmi un nombre fini. Après chaque interview, il faut décider si la personne est engagée ou non. Si oui, le processus se termine (sans voir les autres candidats); sinon, on ne peut ni revenir sur la décision ni recontacter le candidat plus tard". Le but étant évidemment de recruter la meilleure personne, en n'ayant pas de valeur intrinsèque (ce candidat vaut 9/10) mais uniquement sur base de comparaison avec celles vues précédemment. C'est un problème qu'on qualifie de online, une fois un élément considéré, il ne pourra plus l'être par la suite. En l'occurrence, il existe des nombreuses "solutions" à ce problème (et toutes ses variantes) avec une stratégie optimale à appliquer et pour des résultats meilleurs que purement aléatoires2.
Si ce champ d'étude vous intéresse, je ne peux que vous conseiller le livre: Randomized algorithms de R. Motwani et P. Raghavan3 qui présente, avec une rare qualité, une vue fort complète sur ce domaine, que ce soit sur les algorithmes, leurs idées sous-jacentes, leurs cadres théoriques et leurs preuves. Le sujet de cet article est en partie inspiré par le livre introduction to algorithms de Cormen, Leierson, Rivest (le même qui a travaillé sur l'algorithme avec Floyd) et al.4, grand classique de l'algorithmique tant ce livre aborde une quantité astronomique de notions, algorithmes ou d'idées.
Un tout grand merci à @Migwel pour sa relecture.
- YAO, Andrew Chi-Chin. Probabilistic computations: Toward a unified measure of complexity. In : 18th Annual Symposium on Foundations of Computer Science (sfcs 1977). IEEE Computer Society, 1977. p. 222-227.
- BAYÓN, L., AYUSO, P. Fortuny, GRAU, J. M., et al. The Best-or-Worst and the Postdoc problems. Journal of Combinatorial Optimization, 2018, vol. 35, no 3, p. 703-723.
- MOTWANI, Rajeev et RAGHAVAN, Prabhakar. Randomized algorithms. Cambridge university press, 1995.
- CORMEN, Thomas H., LEISERSON, Charles E., RIVEST, Ronald L., et al. Introduction to algorithms. MIT press, 2009.