La notion de barycentre ou de centre de masse est directement empruntée à la physique. Etant donné un ensemble de points massiques, un champ (homogène!) de pesanteur définit en chacun des points une force (le poids) d'intensité proportionnelle à la masse. Le barycentre ou centre de masse est le point d'application de la résultante de cet ensemble de forces parallèles. La résultante a une intensité correspondant à une masse égale à la somme des masses de tous les points du système.

On peut généraliser cette notion en considérant des masses négatives, c'est-à-dire que la force appliquée en un point de masse négative est dirigée en sens opposé à celle appliquée à un point de masse positive.

Si \(a_1, a_2, ..., a_n\) sont n points respectivement affectés de masses \(m_1, m_2, ..., m_n\), le barycentre du système sera le point \(g\) affecté de la masse \(m = \sum\limits_{j=1}^{n} m_j\) (nous supposerons que cette masse \(m\) n'est pas nulle), défini par:

\[ m.og = \sum_{j=1}^{n} m_j.oa_j\]

Pour des raisons physiques évidentes, la définition de ce point g doit être indépendante du choix du point o. Vérifions-le par calcul:

\[ m.o'g' = \sum_{j=1}^{n} m_j.o'a_j \]

On déduit par soustraction :

\[ m.(og-o'g') = \sum_{j=1}^{n} m_j.oa_j -\sum_{j=1}^{n} m_j.o'a_j = \sum_{j=1}^{n} m_j(oa_j-o'a_j) = \sum_{j=1}^{n}m_j.o'o = m.oo'\]

et il en résulte que \(og-o'g' = oo'\), d'où \(og = oo'+o'g' = og'\) et par conséquent \(g = g'\).

On peut "oublier" la position du point \(o\) et donc adopter la notation abrégée :

\[ m.g = \sum_{j=1}^{n} m_j.a_j\]

Si l'on a deux points \(a\) et \(b\) affectés de masses \(\alpha \) et \(\beta \), le barycentre \(g\) sera le point défini par \((\alpha+ \beta).g = \alpha.a + \beta.b \) et sera situé sur la droite \(ab\). De plus, il divisera le segment ab dans le rapport \(\beta/\alpha \) (cf.la théorie des leviers)

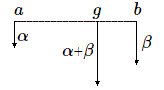
Un simple calcul montre que pour calculer le barycentre d'un ensemble de points massiques, on peut remplacer un sous-ensemble quelconque de points par son barycentre affecté de la masse somme (supposée non nulle).

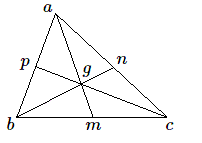Appliquons cette propriété au calcul du barycentre de trois points \(a, b, c\) non alignés affectés de masses égales que nous prendrons comme unité de masse. Le barycentre de \(b, c\) est le milieu \(m\) affecté d'une masse \(2\). Le barycentre de \(m\) et \(a\) sera situé sur la médiane am du triangle \(abc\) et situé aux \(2/3\) de celle-ci. De même si l'on regroupe les points \(c\) et \(a\), on peut les remplacer par leur milieu \(n\) affecté d'une masse \(2\). À nouveau le barycentre du système \(b, n\) sera sur la médiane bn; de même pour la dernière médiane et l'on retrouve le théorème bien connu:

Les trois médianes d'un triangle concourent en un même point (le barycentre) situé aux 2/3 de chacune d'elles.

Généralisons légèrement le cas traité ci-dessus et calculons le barycentre de trois points \(a, b, c\) non alignés affectés de masses \(\alpha, \beta, \gamma \) (de somme non nulle).

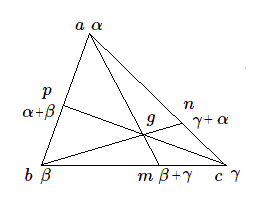Le barycentre de \(ab\) est le point \(p\) (affecté de la masse \(\alpha+\beta \)) qui partage le segment \(ab\) dans le rapport de section \(\beta/\alpha \). Le barycentre du système des trois points est situé sur la droite \(cp\). De même il est situé sur la droite \(am\), où \(m\) est le barycentre des points \(bc\) qui partage le segment \(bc\) dans le rapport \(\gamma/\beta\); enfin il est encore situé sur la droite \(bn\) où \(n\) partage le segment \(ca\) dans le rapport \(\alpha/\gamma\). Les trois droites \(am, bn\) et \(cp\) sont concourantes en un point \(g\), barycentre du système. Inversement si trois droites issues des sommets d'un triangle concourent en un point \(g\), ce point peut être considéré comme le barycentre des trois sommets affectés de masses convenablement choisies en fonction des trois rapports de section dans lesquels les points \(p, m\) et \(n\) partagent les segments \(ab, bc\) et \(ca\).

Ceci est en fait le théorème de Céva :

Trois droites issues des sommets d'un triangle sont concourantes si et seulement si elles déterminent sur les côtés opposés des points partageant ceux-ci dans des rapports de section dont le produit est égal à 1.

Passons à présent au barycentre de 4 points \(a, b, c, d\) affectés de masses que nous supposerons égales à \(1, \lambda, \mu, \lambda\mu\)

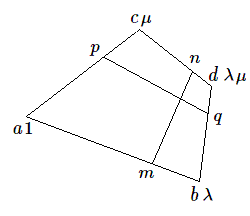Procédons de deux manières différentes en groupant tout d'abord les points \(ab\) et \(cd\) et ensuite les points \(ac\) et \(bd\). Dans le premier cas les barycentres partiels \(m, n\) seront situés sur les côtés \(ab\) et \(cd\) et les partageront dans les mêmes rapports de section \(\lambda \). Le barycentre est un point de la droite joignant les deux points \(mn\). Dans le deuxième cas il sera situé sur la droite joignant les deux points \(p, q\) partageant les côtés \(ac\) et \(bd\) dans le même rapport \(\mu\). Il est par conséquent situé à l'intersection de ces deux droites.

Cette propriété serait inintéressante si l'on travaillait dans le plan, mais rien jusqu'ici ne nous a imposé cette restriction. Nous pouvons fort bien supposer que ces quatre points a, b, c, d ne sont pas situés dans un même plan. Dès lors la propriété devient remarquable, car en général deux droites de l'espace ne se rencontrent pas.

Supposons à présent que nous faisons varier \(\lambda \). La droite \(mn\) varie donc en rencontrant constamment la droite \(pq\). De même si nous faisons varier \(\mu\), c'est la droite \(pq\) qui variera en rencontrant constamment la droite \(mn\). Nous obtenons donc ainsi une surface engendrée par l'ensemble de ces droites: il s'agit d'un paraboloïde hyperbolique .

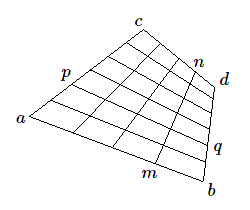
Remarquons pour terminer que toutes les droites \(mn\) sont parallèles au plan parallèle à \(ab\) et \(cd\) et que les droites \(pq\) sont parallèles au plan parallèle à \(ac\) et \(bd\).