Soit T une transformation linéaire, ou application linéaire , d'un plan vectoriel. Elle peut être décrite par les équations donnant les coordonnées ( x', y' ) de l'image du vecteur \((x, y)\) :

\[ \begin{cases} x'=ax+by \\ y'=c x+dy \end{cases}\]

Sous forme matricielle elle s'écrit :

\[ \left\lgroup\matrix{x'\\y'}\right\rgroup = \left\lgroup\matrix{a & b \\ c & d}\right\rgroup \left\lgroup\matrix{x\\y}\right\rgroup \]

Si on préfère décrire l'application par les images des vecteurs de base \(\imath\) et \(\jmath\), il suffit de regarder les images des points \((1,0)\) et \((0,1)\) qui sont les points \((a, c)\) et \((b, d)\); par conséquent, les images \(\imath'\) et \(\jmath'\) des vecteurs de base sont donc les vecteurs :

\[ \begin{cases} \imath' = a \imath + c\jmath \\ \jmath' = b \imath + d\jmath \end{cases} \]

On peut se demander quelle est l'image de plan vectoriel. Ce sera, en général, le plan lui-même sauf si, par un malencontreux hasard, les deux vecteurs images \(\imath'\) et \(\jmath'\) ne sont pas linéairement indépendants. Dans ce cas, cela signifierait que la dimension de l'image est soit 1 (\(\imath'\) et \(\jmath'\) colinéaires), soit 0 (\(\imath'\) et \(\jmath'\) nuls). Dans le cas général, il n'en est pas ainsi; les vecteurs \(\imath'\) et \(\jmath'\) constituent une nouvelle base.

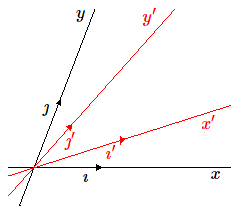
Soit le plan avec l'ancienne base \((\imath, \jmath)\) et la nouvelle \((\imath', \jmath')\). Sur chacune des deux bases, on peut cons- truire un parallélo- gramme mais, en général, leur aire sera différente.

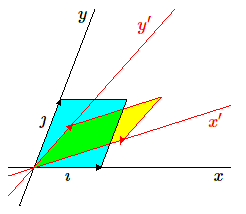
Nous allons calculer le rapport entre ces deux aires. Pour calculer l'aire du parallélogramme construit sur \(\imath'\) et \(\jmath'\), nous utiliserons le fait que l'aire d'un parallélogramme ne varie pas, si un de ses côtés glisse sur lui-même, ce qui, en termes de vecteurs, se traduit par le fait que l'aire est invariante si on ajoute à un des deux vecteurs un multiple \(\mu\) de l'autre. Dans le cas étudié, l'aire du parallélogramme construit sur les vecteurs \(\imath'\) et \(\jmath'\) est la même que celle d'un parallélogramme construit sur \(\imath'\) et \(\jmath' + \mu \imath'\). Comme les coordonnées des vecteurs \(\imath'\) et \(\jmath'\) constituent les colonnes de la matrice T, on voit que cela revient à ajouter à une colonne (la 2e par exemple) un multiple \(\mu\) de l'autre (ici de la première).

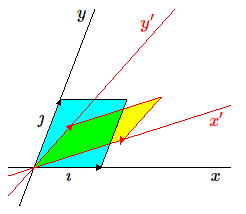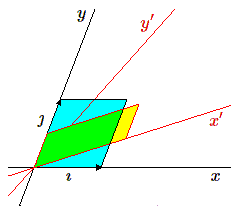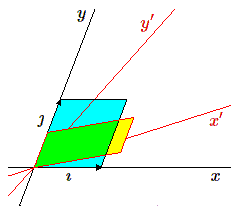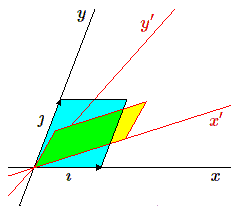Supposons, et c'est le cas général, qu'aucun des deux vecteurs \(\imath', \jmath'\) ne soit dirigé selon un axe coordonné. Nous allons choisir de remplacer le vecteur \(\jmath'\) par un vecteur dirigé suivant cet axe en lui ajoutant un multiple convenable du vecteur \(\imath'\). Soit \(\jmath'' = \jmath' +  \mu \imath'\), le vecteur cherché. En fonction des vecteurs de base \(\imath, \jmath\) on obtient : \(\jmath'' = b\imath + d\jmath +  \mu(a\imath + c\jmath)= (b +  \mu a)\imath + (d +  \mu c)\jmath\). La coordonnée de ce vecteur selon \(\imath\) doit être nulle, ce qui donne  \(\mu = -b/a\) (\(a\) n'est pas nul, sinon \(\imath'\) serait dirigé selon l'axe des \(y\), ce qui est contraire à notre hypothèse); sa coordonnée suivant \(\jmath\) vaut alors \(d +  \mu c = d + (-b/a)c = (ad - bc)/a\).

On doit ainsi calculer l'aire du parallélogramme construit sur \(\imath' = a\imath + c\jmath\) et \(\jmath'' = (ad - bc)/a\jmath\). En ajoutant cette fois au vecteur \(\imath'\) un multiple de \(\jmath''\), on peut évidemment annuler la composante suivant \(\jmath\) et \(\imath'\) peut être remplacé par le vecteur \(\imath'' = a\imath \).

Le problème est ainsi résolu: l'aire \(A(\imath'', \jmath'')\) du parallélogramme construit sur les deux vecteurs: \(\imath'' = a\imath\) et \(\jmath'' = (ad - bc)/a \jmath\) est égale à \(A(\imath', \jmath')\). Elle vaut \(a(ad - bc)/a.A(i, j) = (ad - bc).A(\imath, \jmath)\). Si nous prenons le parallélogramme construit sur \(\imath, \jmath\) comme unité d'aire, \(ad - bc\) est l'aire de son transformé par l'application linéaire \(T\).

Il est important de remarquer que le déterminant d'une matrice 2 x 2, \(ad - bc\) est le même que celui de la matrice, dite transposée, obtenue en permutant lignes et colonnes. Remarquons que dans le cas où la transformation n'est pas une permutation (si la matrice est de rang 1 ou 0, c'est-à-dire si les vecteurs \(\imath'\) et \(\jmath'\) sont colinéaires ou nuls) l'aire \(A(\imath', \jmath')\) est évidemment nulle.

De même, à trois dimensions, le déterminant de la matrice 3 x 3 d'une application linéaire représente la mesure du volume \(V(\imath', \jmath', k')\) du parallélépipède construit sur les 3 vecteurs images des vecteurs de base, l'unité étant \(V(\imath, \jmath, k)\).

Ces remarques permettent de comprendre facilement que la valeur d'un déterminant est invariante si on ajoute à une rangée une combinaison linéaire des autres. On dispose ainsi d'une manière simple d'en calculer la valeur (par exemple par triangulation).