Le paradoxe des anniversaires est un problème classique de statistiques qui cherche à répondre à la question suivante:
Combien de personnes doit-on rassembler dans une même pièce pour qu’il devienne plus probable que deux d’entre elles partagent la même date d’anniversaire plutôt que l’inverse ?
$$ \mathbb{P}(\text{au moins 2 personnes partagent la même date d'anniversaire}) \geq 0.5 $$Il est d’usage de considérer deux hypothèses:
- Toutes les dates d’anniversaire sont équiprobables ;
- Une année comporte 365 jours ;
Le problème de cette formulation est qu’il faut considérer tous les cas où deux personnes partagent une même date, mais également où trois personnes ont leur anniversaire en commun, … et ainsi de suite jusqu’à \(n\). Il est préférable de poser la question inverse:
Quelle est la probabilité qu’aucune personne ne partage le même anniversaire ?
$$ 1 - \mathbb{P}(\text{qu'aucune personne ne partage la même date d'anniversaire}) \leq 0.5 $$Cette question est bien plus simple à résoudre puisqu’il suffit de considérer ce qu’il se passe dès qu’une nouvelle personne rentre dans la pièce.
- Au début, il n’y a personne, la première personne peut avoir son anniversaire n’importe quand, il y a \(365/365\) choix possibles.
- Une deuxième personne rentre, une date possible n’est plus disponible, il lui reste \(364/365\) choix possibles.
- Et ainsi de suites,
- La \(n\)e personne n’a le choix qu’entre \((365 - (n - 1)) / 365\) possibilités.
Avec un peu de symbolique, on obtient que la formule générale est de la forme:
$$ \prod_{k = 0}^{n - 1} \frac{365 - k}{365} $$Il ne reste plus qu’à déterminer quand cette équation donne un résultat proche de notre valeur cible: 0.5. Mais comment ?
Méthode approximative
Au lieu d’essayer des valeurs au hasard de \(n\) afin de trouver pour lesquelles la valeur de notre formule est la plus proche de 0.5. On peut se demander s’il est possible d’approximer la solution qui devrait exister.
La difficulté du problème vient du fait que notre variable \(n\) fait partie intégrante de l’équation. Il faut trouver un moyen d’isoler cette variable dans notre équation. Une astuce classique, quand on se retrouve avec une produit, consiste à employer la fonction logarithme afin de transformer les multiplications en additions. On se retrouve avec:
$$ \log{\frac{1}{2}} \approx \log{\prod_{k = 0}^{n - 1} \frac{365 - k}{365}} = \log{\prod_{k = 0}^{n - 1} (1 - \frac{k}{365})} $$Or, on sait que \(\log{a} + \log{b} = \log{ab}$. On peut transformer ce produit en somme:
$$ \log{\frac{1}{2}} \approx \sum_{k = 0}^{n - 1} \log{(1 - \frac{k}{365})} $$Si \(n\) est petit, on peut chercher à approximer l’expression: \(\log{(1 - \frac{k}{365})}\) en employant la définition de la série de Taylor-Maclaurin de la fonction logarithme.
On "sait" que:
$$ \log{1 + x} \approx x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + ... $$Si on omet les termes de degrés supérieurs à 1, et qu’on dit qu’ils tendent vers 0 comme (\((\frac{k}{365})^2 \approx 0\) si \(k\) est petit). On remplace brutalement dans notre équation, et on obtient l’expression suivante:
$$ \log{\frac{1}{2}} \approx \sum_{k = 0}^{n - 1} \frac{-k}{365} $$Si on applique la formule du quotient de logarithme et simplifie les signes "-", on obtient:
$$ \log{2} \approx \sum_{k = 0}^{n - 1} \frac{k}{365} $$Sur la partie de droite, on repère une formule bien célèbre, la somme des premiers entiers positifs de Gauss.
$$ \log{2} \approx \frac{1}{365} \sum_{k = 0}^{n - 1} k \\ \Leftrightarrow 0.69 \approx \frac{1}{365} \frac{n (n - 1)}{2} $$Si on passe tout du même côté, on obtient une équation du deuxième degré:
$$ n^2 - n - 506 = 0 = (n - 23)(n + 22) $$Ce qui laisse la solution positive: \(n = 23\).
Méthode exacte
On peut écrire un petit script en python pour trouver ce nombre de personnes.
def birthday_paradox(x):
if n > 365:
return 1.0
probability_all_distinct = 1.0
for k in range(n):
probability_all_distinct *= (365 - k) / 365
return 1 - probability_all_distinct
On obtient le graphique suivant:
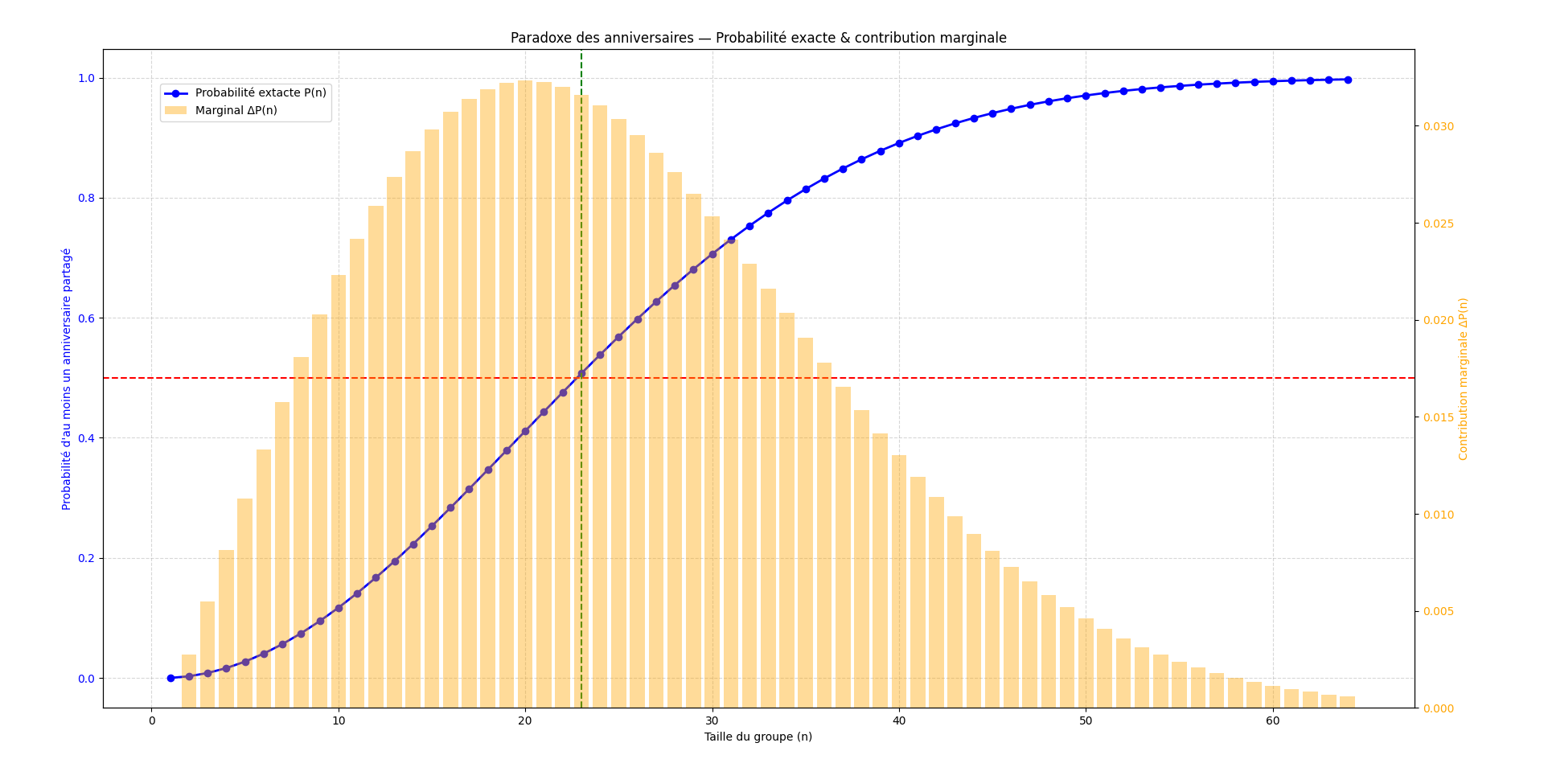
La moyenne est 24.6 et le mode est de 20.
Paradoxe de mon anniversaire ?
Une variante de ce problème consiste à se demander d’un point de vue personnel :
Combien de personnes doit-on rassembler dans une même pièce pour qu’il devienne plus probable qu’au moins une personne partage ma même date d’anniversaire plutôt que l’inverse ?
$$ \mathbb{P}(\text{qu'au moins une personne partage ma même date d'anniversaire}) \geq 0.5 \Leftrightarrow $$ $$ 1 - \mathbb{P}(\text{qu'aucune personne ne partage ma même date d'anniversaire}) \leq 0.5 $$On considère ce qu’il se passe dès qu’une nouvelle personne rentre dans la pièce.
- Au début, la première personne doit éviter mon anniversaire, il y a \(364/365\) choix possibles.
- Une deuxième personne rentre, et, … il se produit la même chose, en effet, on ne s’intéresse pas au cas où ils partageraient la même date d’anniversaire.
- Et ainsi de suites,
- La \(n\)e personne a toujours le choix entre \(364/365\) possibilités.
On se retrouve avec:
$$ \frac{1}{2} \approx (\frac{364}{365})^{n} $$On réapplique notre astuce des logarithmes, et on obtient:
$$ \frac{1}{2} \approx n (\log{364} - \log{365}) \\ \Leftrightarrow n = \frac{\log{2}}{\log{365} - \log{364}} $$Ce qui donne \(n = 252.65\).
Paradoxe de tous les anniversaires ?
Une question nettement plus méchante serait la suivante :
Combien de personnes doit-on rassembler dans une même pièce pour qu’il devienne plus probable qu'il y ait au moins m jours sur lesquels au moins deux d’entre elles partagent la même date d’anniversaire plutôt que l’inverse ?
Autrement dit, il existe m jours dans l'année dans laquelle au moins 2 personnes ont leur anniversaire.
Ce problème est plus connu sous le nom des boules dans les urnes (Balls into bins problem).
Dans notre cas:
- \(U\) urnes identiques
- \(n\) boules réparties uniformément au hasard dans ces urnes (chaque boule choisit une urne indépendamment, probabilité \(1/U\)).
- On veut qu'au moins \(u\) urnes contiennent au moins \(k\) boules.
Pour une urne donnée, le nombre de boules reçue suit une loi binomiale:
$$ X \sim \text{Binomial}(n, 1 / U) $$En particulier:
$$ p_{k} = \mathbb{P}(X \geq k) = \sum_{i=k}^{n} \binom{n}{i} \frac{1}{U}^{i} (1 - \frac{1}{U})^{n - 1} $$represente la probabilité qu'une urne donnée ait au moins \(k\) boules.
Sur lequel, le choix des urnes est aussi indépendant !
$$ Y \sim \text{Binomial}(U, p_{k}) $$Ce qui donne au final:
$$ \mathbb{P}(Y \geq u) = \sum_{j=u}^{U} \binom{U}{j} p_{k}^{j} (1 - p_{k})^{U - j} $$Si on cherche à calculer le nombre minimal de personnes \(n\) qu'il faut pour qu'il y au moins \(u\) jours avec au moins \(k=2\) anniversaires en même temps. On obtient le graphique suivant:
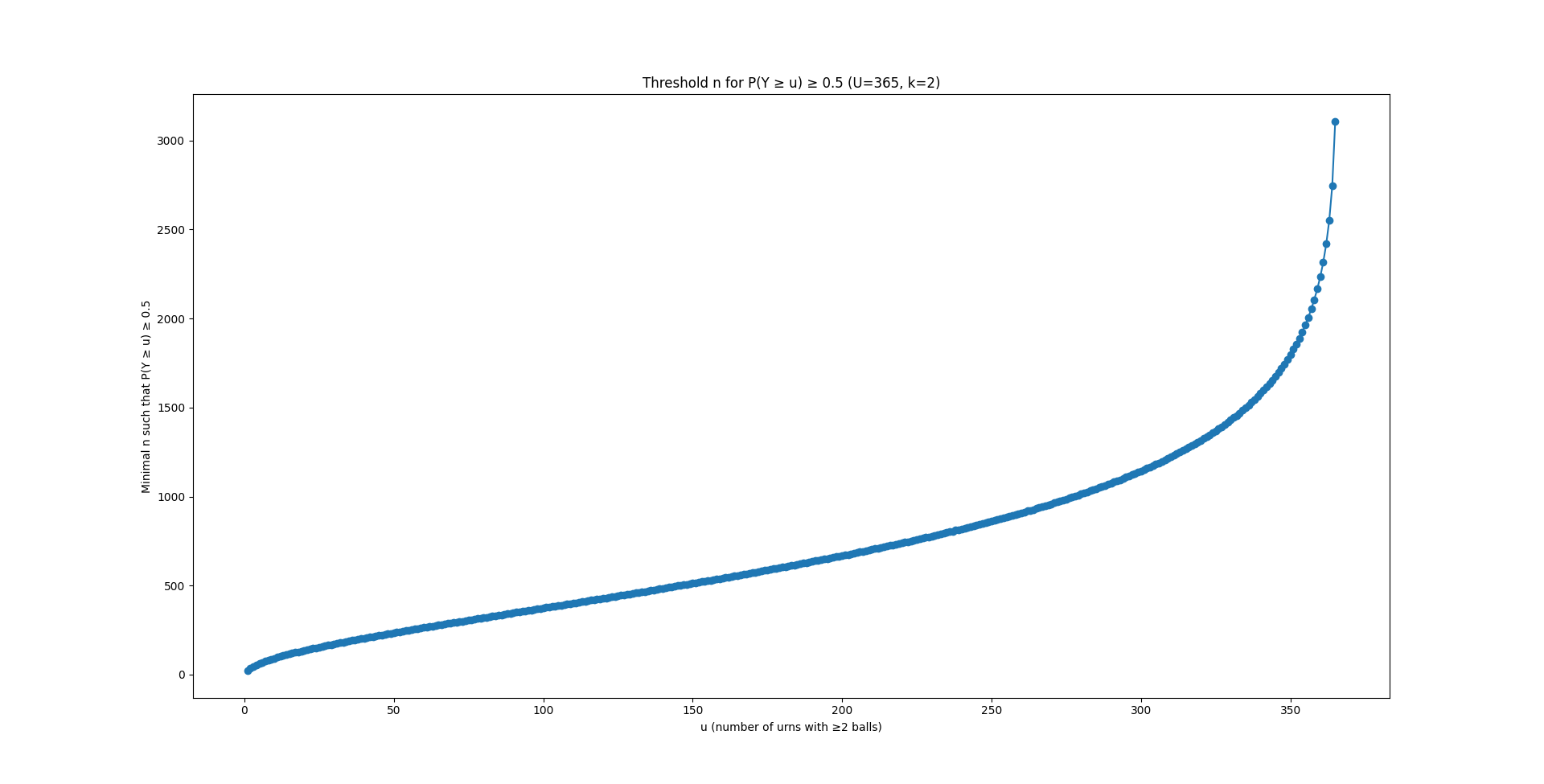
Afin de s'assurer de la justesse des résultats, on peut approximer par la formule de Poisson. Quand \(n\) est grand, on peut approximer \(X\) par une loi de Poisson de paramètre \(\lambda = \frac{n}{365}\). Alors:
$$ p_{k} = \mathbb{P}(X = k) \approx e^{\lambda} \frac{\lambda^{k}}{k!} $$Donc:
$$ \mathbb{P}(X \geq k=2) = 1 - p_{0} - p_{1} \approx 1 - e^{\lambda} - \lambda e^{-\lambda} = 1 - e^{-\lambda}(1 + \lambda) $$En supposant l'indépendance entre les jours, la probabilité que tous les jours aient au moins 2 personnes est approximée par :
$$ p_{n} = (1 - e^{-\lambda}(1 + \lambda))^{365} ~ \text{où} ~ \lambda = \frac{n}{365} $$On cherche quand on a au moins 50%:
$$ p_{n} \geq 0.5^{1/365} $$On obtient que:
$$ (1 - e^{-\lambda}(1 + \lambda)) \approx 0.9981 \Leftrightarrow e^{-\lambda}(1 + \lambda) \approx 0.0019 $$Pour \(\lambda \approx 8.5\), on obtient 0.00193 (proche du 0.0019). L'approximation de \(n\) est donc donné par \(n \approx 8.5 * 365 \approx 3100\).
Paradoxe des naissances
Un autre paradoxe bien connu et peu intuitif consiste à poser la question suivante:
Anne a deux enfants dont un est un garçon. Quelle est la probabilité que l’autre enfant soit une fille ?
Intuitivement, on aurait envie de dire que le sexe de l’enfant est un événement indépendant et donc que la probabilité devrait être 50%. Mais, il faut se référer à la définition des probabilités, au nombre de cas sur le nombre de cas possibles.
On se retrouve avec la matrice suivante:
| Fille | Garçon | |
|---|---|---|
| Fille | FF | FG |
| Garçon | GF | GG |
Or, le cas FF est impossible, puisque l’on sait que Anne possède au moins un garçon. La probabilité est donc de \(2/3\).
Variante du paradoxe des naissances
La variante du paradoxe consiste à poser la question suivante:
Anne a deux enfants dont un est un garçon qui est né un Jeudi. Quelle est la probabilité que l’autre enfant soit une fille ?
Il n’est vraiment pas facile de saisir pourquoi la date de naissance de l’enfant aurait une influence sur la probabilité, mais c’est bel et bien le cas …
On note le jour de la semaine par son indice (1 = lundi, 2 = mardi, …, 4 = jeudi, …). On se retrouve avec la matrice suivante:
| GG | FG | GF | |
|---|---|---|---|
| G1G4 | G1G4 | F1G4 | G4F1 |
| G2G4 | G2G4 | F2G4 | G4F2 |
| G3G4 | G3G4 | F3G4 | G4F3 |
| G4G4 | F4G4 | G4F4 | |
| G5G4 | G5G4 | F5G4 | G4F5 |
| G6G4 | G6G4 | F6G4 | G4F6 |
| G7G4 | G7G4 | F7G4 | G4F7 |
On remarque qu’il faut éviter de compter deux fois l’événement \(G4G4\) comme on n’a déjà considéré le cas où les deux garçons sont nés le même jeudi.
On se retrouve avec 14 cas (les colonnes FG et GF) sur les 27 possibilités. Cela donne \(14/27 \approx 51.9\)%