Ce genre d’expériences où chaque jour correspond à une nouvelle expérience, indépendante de la veille et où le résultat est binaire (vinaigrette ou mayonnaise) est qualifié de processus de Bernouilli.

Ici, au lieu d'avoir une distribution de Bernouilli connue (probabilité d'avoir vinaigrette = \(p\)% et mayonnaise = (1 - \(p\)%) = q%), celle-ci est inconnue. L'expérience est également répétée \(n\) fois; on se retrouve plutôt dans le cas d'une distribution Binomiale à paramètres inconnus.

Pour rappel, la probabilité d'avoir exactement \(k\) 'succès' au bout de \(n\) expériences et est donné par la formule suivante:

$$ Pr(k; n, p) = \binom{n}{k} p^{k} (1 - p)^{n - k} $$

Le problème devient inverse. Pour quelle valeur de \(p\), la probabilité de nos observations est-elle maximale ? Quelle est la valeur la plus probable pour \(p\) afin d’obtenir nos résultats. C’est une approche qu’on qualifie d'inférence bayésienne.

En essayant d’optimiser la valeur de \(p\) par les techniques de maximum likelihood estimator ou celles des moments, nous arrivons à un estimateur qui est également optimal ¹:

$$ \hat{p} = \frac{k}{n} $$

Cela fait sens que le meilleur estimateur de la probabilité que nous avons soit le rapport du nombre de succès (\(k\)) sur le nombre de tentatives réalisées (\(n\)).

Un intervalle de confiance sur une distribution binomiale peut être donnée par une approximation de la (distribution) normale, aussi appelé "intervale de Wald"². On a que:

$$ p \approx \hat{p} \pm \frac{z_{\alpha}}{\sqrt{n}} \sqrt{\hat{p} (1 - \hat{p})} $$

où \(z_{\alpha}\) est le quantile de la distribution normale (95% = 1.96). On retrouve bien la relation étroite qu’entretient la distribution normale et binomiale dans cette relation.

Mais est-il possible de modéliser la distribution de probabilité la plus probable pour un \(p\) connu dans le cadre d’une loi binomiale ?

On cherche une distribution telles que:

• elle soit définie entre 0 et 1 (ce sont des probabilités que l'on cherche);
• positive;
• l'intégrale doit être égale à 1;
• la moyenne devrait être proche de notre \(\hat{p}\);
• ainsi que l'erreur \(var[\hat{p}]\);
• chaque élément est indépendant et identiquement distribué;

La distribution qui correspond à ces propriétés est la distribution Beta:

$$ \begin{aligned} f(x; \alpha, \beta) & = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha - 1} (1 - x)^{\beta - 1} \\ & = \frac{1}{\Beta(\alpha, \beta)} x^{\alpha - 1} (1 - x)^{\beta - 1} \end{aligned} $$

Plusieurs remarques:

• \(\Gamma(z)\) est la fonction "Gamma", la généralisation de la fonction exponentielle (\(\Gamma(z) = (z - 1)!\));
• \(\Beta(z_{1}, z_{2})\) est la fonction "Beta", qui peut s'interpréter comme la généralisation des coefficients binomiaux;
• \(\alpha\) est généralement considéré comme le nombre de succès \(k\) "+ 1", \(\beta\) est le nombre d'échecs (\(n - k\)) "+ 1". Ces "+ 1" apparaissent notamment à cause de la définition de ces fonctions \(\Gamma\) et \(\Beta\);
• On peut remarquer une très grande symétrie dans cette définition et celle de la Binomiale;

Cette distribution possède plusieurs bonnes propriétés:

• \(E[X] = \frac{\alpha}{\alpha + \beta}\). Si l'on remplace les valeurs de \(\alpha\) et \(\beta\) par nos observations, nous obtenons: \(\frac{k + 1}{n + 2}\) qui, lorsque \(n\) tend vers l'infini, retombe sur notre \(\hat{p}\);
• \(var[X] = \frac{\alpha \beta}{(\alpha + \beta)^{2}}(\alpha + \beta + 1)\). Avec nos valeurs, on a: \(\frac{(k + 1) * (n - k + 1)}{(n+2)^{2}(n + 3)}\) et à la limite: \(\sigma^{2} \approx \frac{\hat{p}(1 - \hat{p})}{n}\) qui est ce que l'on recherchait;
• Le mode \(= \frac{\alpha - 1}{\alpha + \beta - 2}\) est exactement notre \(\hat{p}\), ce qui tombe bien puisque c'est là où la probabilité est maximale. La moyenne peut être très légèrement décalée par rapport au mode à cause du côté où penche la queue;

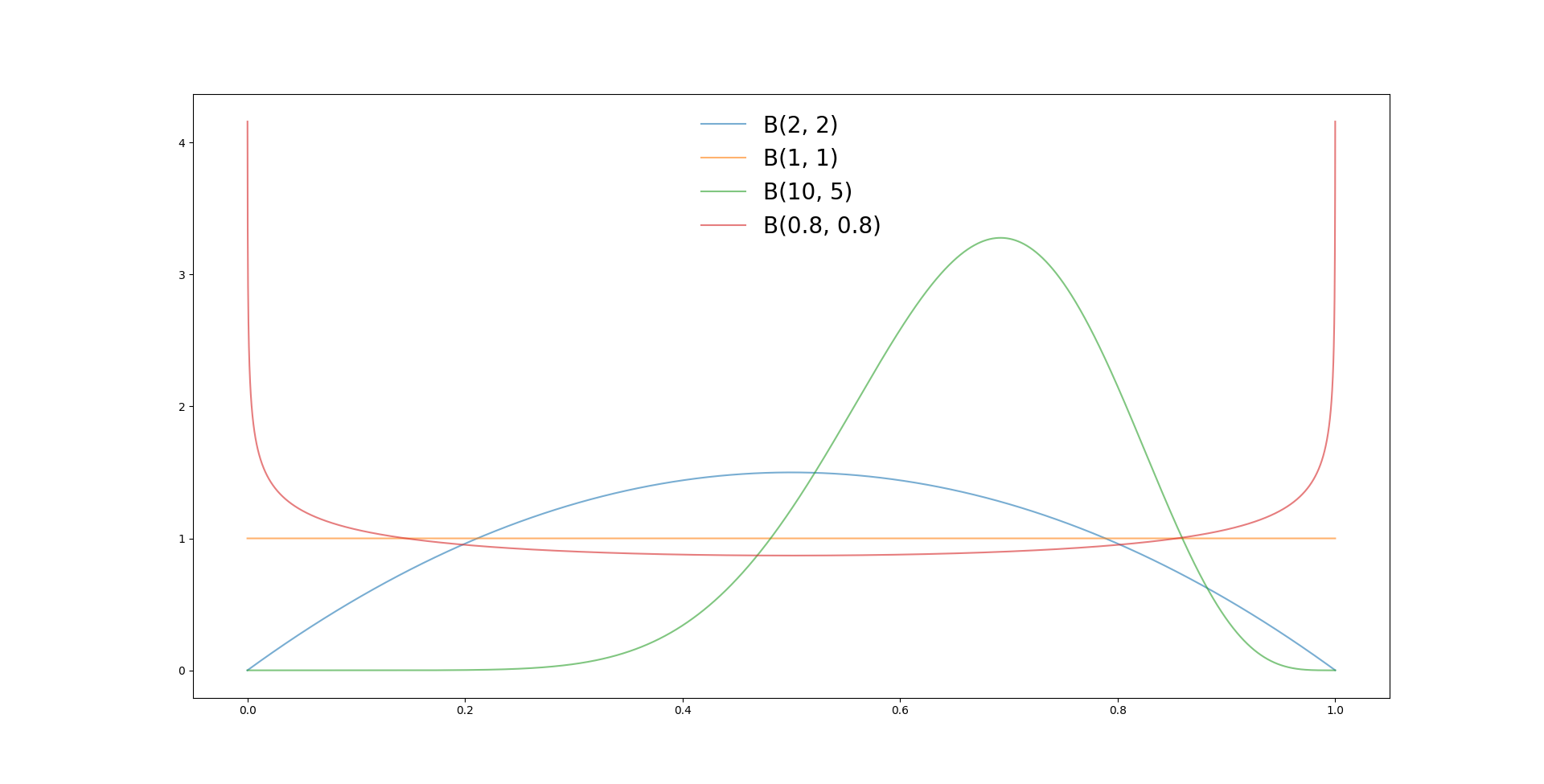
Par exemple, nous voyons que:

• Pour \(B(1, 1)\), comme il n'y a eu ni succès, ni échec, la distribution est constante sur tout le domaine. Aucune probabilité n'est préférée a priori;
• Pour \(B(2, 2)\), on voit la courbe se centrer à la moitié mais avoir une base relativement large (\(\sigma\));
• Pour \(B(10, 5)\), on commence à pencher vers une probabilité vers 2/3 et l'on observe un pic bien plus resserré pour cette valeur;
• Lorsque l'on met des valeurs de \(\alpha\) ou \(\beta\) inférieure à 1, les probabilités deviennent très polarisées, très extrêmes;

Vous reconnaîtrez que c'est un outil puissant de statistique a priori, qui permet une analyse bien plus puissante que la donnée brute par elle-même.

Il est naturel de se demander comment ce concept peut être étendu. Une direction possible est d'étudier sa généralisation à plusieurs variables.

Supposons que vous effectuiez un relevé des causes d'admission à l'hôpital. Vous savez que les gens peuvent se retrouver dans l'une des \(K\) catégories. Vous vous demandez à quel point ses résultats sont représentatifs de la population. Est-il possible d'obtenir également des marges d'erreur sur notre échantillon ?

On peut définir la distribution de Dirichlet Dir(\(\alpha\)):

$$ f(x; \alpha) = \frac{1}{\Beta(\alpha)} \prod_{i=1}^{K} x_{i}^{\alpha_{i} - 1} $$

où

$$ \Beta(\alpha) = \frac{\prod_{i=1}^{K} \Gamma{(\alpha_{i})}}{\Gamma(\alpha_{0})} \quad et \quad \alpha_{0} = \sum_{i=1}^{K} \alpha_{i} $$

Cela peut sembler extrêmement barbare à première vue, mais décomposons les morceaux:

• \(\alpha_{0} = \sum_{i=1}^{K} \alpha_{i}\), on définit \(\alpha_{0}\) comme la somme de nos valeurs \(\alpha_{i}\), nos observations.
• \(\Beta(\alpha) = \frac{\prod_{i=1}^{K} \Gamma{(\alpha_{i})}}{\Gamma(\alpha_{0})}\), on retrouve une génération des coefficients multi-nomiaux.
• \(\frac{1}{\Beta(\alpha)} \prod_{i=1}^{K} x_{i}^{\alpha_{i} - 1}\), toutes nos probabilités \(x_{i}\).

Attention qu'il faut que toutes nos probabilités \(x_{i}\) soit comprises entre 0 et 1 et que leur somme soit égale à 1 (\(\sum_{i=1}^{K} x_{i} = 1\)).

On peut effectuer deux observations:

• Si \(K = 2\), on retombe bien sur la distribution Beta.
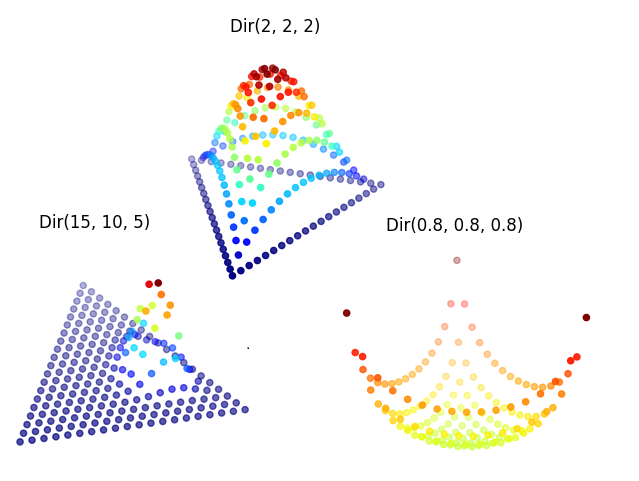
• Cet ensemble de \(x_{i}\) forme ce qu'on appelle un simplex, la généralisation d'un triangle sur plusieurs dimensions.

Attention que ces trois distributions font toute l’hypothèse que les évènements sont indépendants et identiquement distribués.

Si l’on pioche au sein d’une boîte contenant un nombre fini de balles, sans remplacement, on obtient:

• Binomiale => Hypergéométrique
• Beta => Beta-binomiale
• Dirichlet => Dirichlet-multinomiale

À noter qu’il y a tout un ensemble de subtilités qui peuvent s’adjoindre à ces notions. Par exemple, il existe la distribution categorical quand les observations peuvent faire partie de \(K\) catégories. S’intéresse-t-on aux distributions a priori et non a posteriori, sur un échantillon ou sur toute la population ?

Bref, je voulais surtout présenter comment une tentative de réponse à la question des marges d’erreurs sur les résultats obtenus et comment avoir une meilleure idée des paramètres sous-jacents du modèle sur base d’un résultat.