Pour l’Épiphanie (et aussi le reste du mois de janvier), il est d'usage de manger de la galette des rois. La tradition veut que l'on cache une fève à l'intérieur, et la personne qui tombe desuss devient le roi ou la reine le temps du repas.
Malheureusement, il arrive que la découpe des parts révèle l’emplacement de la fève ! La surprise peut alors être gâchée, pour peu que la découpe se fasse devant les mangeurs.
Quelle est la probabilité de couper sur la fève ? Et surtout, comment faire en sorte de la réduire ?
Hypothèses
Pour calculer des probabilités, il faut d’abord bien définir le problème que l’on cherche à résoudre. Pour cela, il est nécessaire d'exprimer quelques hypothèses sur notre problématique:
- La galette est assimilable à un disque de rayon 1 (\(R_{g}\)).
- La fève est approximée par un disque de rayon inférieur à 1 (\(R_{f}\)).
- La galette sera découpée en \(n\) parts égales selon des demi-droites passant par le centre de la galette (\(O\)).
- Le centre de la fève est placé selon une loi de probabilité uniforme dans le disque centré en \(O\) et de rayon \(R_{g} - R_{f}\).
En pratique, la loi est rarement uniforme puisqu'on a tendance à placer la fève proche du bord.
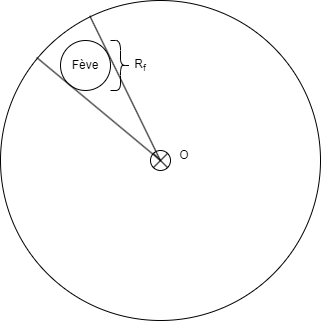
En pratique, il sera plus simple d'exprimer le rapport de la galette à celui de la fève \(\frac{R_{g}}{R_{f}}\). Ex: si \(\lambda = 10\), cela voudra dire que la fève est 10x plus petite que la galette.
On cherche à exprimer cette probabilité en fonction de \(n\) (le nombre de parts) et \(\lambda\) (le rapport): \(P(n, \lambda)\).
Une simple coupe
Pour rappel, la probabilité d'un événement est le rapport entre le nombre de réalisations possibles d'un événement sur le nombre total de situations.
Dans notre cas, on souhaite connaître la probabilité de l’événement « couper sur la fève ». Il nous faut donc déterminer le nombre de situations dans lesquelles on coupe sur la fève ainsi que le nombre total de situations (celles dans lesquelles on tombe sur la fève, ou pas).
Ici, le nombre de situations possibles est difficilement quantifiable puisque nous avons affaire à des quantités infinies.
Les situations où on coupe sur la fève sont celles où la découpe tombe dans le secteur de la galette occupé par la fève. Le « nombre » de telles situations est donc la taille angulaire du secteur occupé par la fève. On voit ici que la forme exacte de la fève importe peu, seulement l’angle occupé. On notera \(\alpha\) cet angle.
Pour calculer cet angle, il "suffit" de calculer l'angle qu'effectuent les deux tangentes à notre fève par rapport au centre de la galette.
En pratique, ce type de calculs est particulièrement peu élégant et nécessite une autre approche, plus globale ...
Approche générale
On observe que si la fève recouvre le centre de la galette, alors nous ne serons pas en mesure de couper notre galette proprement. Il en va de même si la fève ressort de la galette.
Comme notre distribution est uniforme, il suffit de prendre les rapport entre les différentes couronnes. Ici, on calcule la probabilité que la fève soit trop proche du centre:
$$ p_{invalide} = \frac{\pi R_{f}^{2}}{\pi (R_{g} - R_{f})^{2}} = \frac{R_{f}^{2}}{(R_{f}(\frac{R_{g}}{R_{f}} - 1))^{2}} = \frac{1}{(\lambda - 1)^{2}} $$La probabilité que l'on ne soit pas dans cette couronne interdite est son complémentaire:
$$ p_{valide} = 1 - p_{invalide} = \frac{\lambda (\lambda - 2)}{(\lambda - 1)^{2}} $$Maintenant, plaçons-nous dans la position où la fève est située dans la couronne valide et reprenons les calculs de l'angle du secteur.
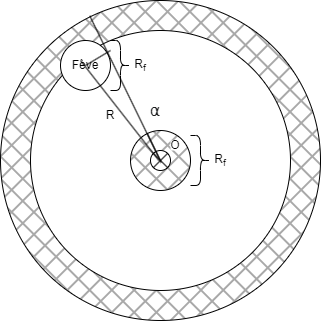
Pour se simplifier la vie, nous ne calculerons l'angle \(\alpha\) qu'avec une seule tangente de notre fève comme la situation est symétrique par rapport au centre \(O\). On se retrouve avec un triangle rectangle formé par le centre de la fève, le point d'intersection d'une des deux tangentes et l'origine. Et, notons \(R\) la distance du centre de la fève à l'origine \(O\).
$$ \sin(\frac{\alpha}{2}) = \frac{R_{f}}{R} \iff \alpha(R) = 2 \arcsin(\frac{R_{f}}{R}) $$Maintenant, remarquons que le problème est assez symétrique, tentons d'appliquer une transformée des coordonnées cartésiennes en coordonnées polaires telles que:
$$ \begin{cases} X = R \cos \Theta\\ Y = R \sin \Theta\\ \end{cases} $$Notre couronne valide avait pour densité de probabilité l'expression suivante:
$$ p_{(X, Y)}(x, y) = \frac{1}{\pi ((R_{g} - R_{f})^{2} - R_{f}^{2})} $$En polaire, l'expression devient assez similaire:
$$ p_{(R, \Theta)}(r, \theta) = \frac{r}{\pi ((R_{g} - R_{f})^{2} - R_{f}^{2})}, \text{avec} R_{f} \leq r \leq (R_{g} - R_{f}) \text{ et } 0 \leq \theta \leq 2 \pi $$N'oublions pas que l'aire de \(dxdx\) devient \(rdrd\theta\) en polaire (Jacobien).
Et maintenant sur tout le cercle, la densité de probabilité de \(p_{R}(r)\) est:
$$ p_{R}(r) = \int_{0}^{2\pi} p(r, \theta) d\theta = \frac{2r}{((R_{g} - R_{f})^{2} - R_{f}^{2})}, \text{avec} R_{f} \leq r \leq (R_{g} - R_{f}) $$La probabilité que notre coupe de la galette d'angle \(\phi\) touche la fève lorsque la fève est à une distance \(R = r\) de \(O\) est égale à la probabilité que \(\Theta\) appartienne, module \(2\pi\), au secteur angulaire \([\phi - \frac{\alpha(r)}{2\pi}, \phi + \frac{\alpha(r)}{2\pi}]\), soit \(\frac{\alpha(r)}{2\pi}\).
Et ceci est vrai pour toutes les parts. Plus, nous effectuerons de découpes égales, plus cet angle \(\phi\) deviendra petit et est exprimé comme \(\frac{2k\pi}{n}\) avec \(k = 0, 1, ..., n - 1\).
On se retrouve avec l'expression suivante:
$$ P_{\text{intersection}}(r) = \min(1, \frac{n \alpha(r)}{2\pi}) = \min(1, \frac{n}{\pi} \arcsin(\frac{R_{f}}{R})) $$Ensuite, on applique de manière très méchante nos formules. Nous nous retrouvons avec:
$$ P_{(\text{intersection | cas valide})} = \int_{R_{f}}^{R_{g} - R_{f}} \min(1, \frac{n}{\pi} \arcsin(\frac{R_{f}}{r})) p(r) dr $$On se retrouve avec l'expression partiellement résolue:
$$ P_{(\text{intersection | cas valide})} = \frac{2}{((R_{g} - R_{f})^{2} - R_{f}^{2})} \int_{R_{f}}^{R_{g} - R_{f}} \min(1, \frac{n}{\pi} \arcsin(\frac{R_{f}}{r})) r dr $$Cette fonction \(\min\) peut être décomposée en deux parties. En effet, la probabilité d'intersection de notre fève est égale à 1 si \(\frac{n}{\pi} \arcsin(\frac{R_{f}}{r}) \geq 1\).
$$ \begin{cases} \int r dr \text{ if } \frac{n}{\pi} \arcsin(\frac{R_{f}}{r}) \geq 1 \iff \frac{R_{f}}{r} \leq \sin{\frac{\pi}{n}} \\ \int \frac{n}{\pi} \arcsin(\frac{R_{f}}{r}) r dr \\ \end{cases} $$On intègre les deux branches de la condition:
$$ \begin{cases} \frac{r^{2}}{2} + C \text{ if } \frac{R_{f}}{r} \leq \sin{\frac{\pi}{n}} \\ \frac{n}{2 \pi} (R_{f} r \sqrt{1 - \frac{R_{f}^{2}}{r^{2}}} + r^{2} \arcsin(\frac{R_{f}}{r})) + C \\ \end{cases} $$Ici, la quantité qui nous intéresse est le rapport \(\frac{R_{f}}{r}\), effectuons un changement de variable en \(x\):
$$ x = \frac{R_{f}}{r} \iff r = \frac{R_{f}}{x} $$Les expressions deviennent:
$$ \begin{cases} \frac{1}{2x^{2}} + C \text{ if } x \leq \sin{\frac{\pi}{n}} \\ \frac{n}{2 \pi x} (\sqrt{1 - x^2} + \frac{\arcsin(x)}{x}) + C \\ \end{cases} $$Il nous reste plus qu'à évaluer ces intégrales aux bornes. On se souvient que: \(R_{g} - R_{f} = R_{f}(\lambda - 1)\), en \(r\). En \(x\), les bornes deviennent entre \(1\) et \(\frac{1}{\lambda - 1}\). On sait également que \(\lambda\) est positif, on peut fusionner nos intégrales en l'expression suivante:
$$ [\frac{1}{2x^{2}}]^{1}_{\sin(\frac{\pi}{n})} + [\frac{n}{2 \pi x} (\sqrt{1 - x^2} + \frac{\arcsin(x)}{x})]^{\sin(\frac{\pi}{n})}_{\frac{1}{\lambda - 1}} $$ $$ \frac{1}{2}(1 - \frac{1}{\sin^{2}(\frac{\pi}{n})}) ~ + ~ \frac{n}{2 \pi} [(\frac{\cos(\frac{\pi}{n})}{\sin(\frac{\pi}{n})} + \frac{\frac{\pi}{n}}{\sin(\frac{\pi}{n})^{2}}) - (\frac{\sqrt{1 - (\frac{1}{\lambda - 1})^{2}}}{\frac{1}{\lambda - 1}} + \frac{\arcsin(\frac{1}{\lambda - 1})}{(\frac{1}{\lambda - 1})^{2}})] $$On simplifie les \(\sin(\frac{\pi}{n})^{2}\) et on se retrouve avec:
$$ \frac{1}{2} + \frac{n}{2 \pi} [(\frac{\cos(\frac{\pi}{n})}{\sin(\frac{\pi}{n})} - (\lambda - 1) (\sqrt{\lambda (\lambda - 2)} + (\lambda - 1)\arcsin(\frac{1}{\lambda - 1}))] $$Au final, on cherche à calculer la probabilité suivante:
$$ P(n, \lambda) = P(\text{cas invalide}) + P(\text{intersection | cas invalide}) * P(\text{cas valide}) $$On combine le tout, et on finit par obtenir la solution suivante:
$$ P(n, \lambda) = \frac{n}{\pi}(\arcsin(\frac{1}{\lambda - 1}) + \frac{\sqrt{\lambda (\lambda - 2)} - \frac{\cos{(\frac{\pi}{n})}}{\sin{(\frac{\pi}{n})}}}{(\lambda - 1)^{2}}) \chi(\lambda) + (1 - \chi(\lambda)) $$Avec:
$$ \chi(\lambda) = \begin{cases} 1 & \text{if} \lambda \geq 1 + \frac{1}{\sin(\frac{\pi}{n})}\\ 0 & \text{otherwise}\\ \end{cases} $$Remarques
Des équations, on peut tirer de nombreuses conclusions qui confirment notre intuition:
- Il faut placer la fève le plus proche du bord possible afin de minimiser la section angulaire ;
- Plus la fève est petite par rapport au gâteau, moins on a de chance de tomber dessus ;
- La forme importe peu, il suffit de la placer radialement, dans le sens le plus étroit ;
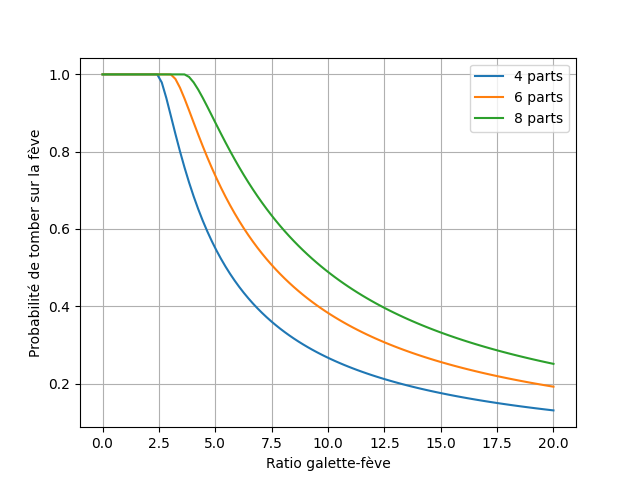
On peut essayer de tester numériquement notre solution afin de s'assurer de sa validité, en simulant la découpe de nombreuses galettes.
On obtient bien les mêmes courbes !
On peut se demander comment évolue la probabilité de tomber sur la fève en fonction d'où est placée cette fève.
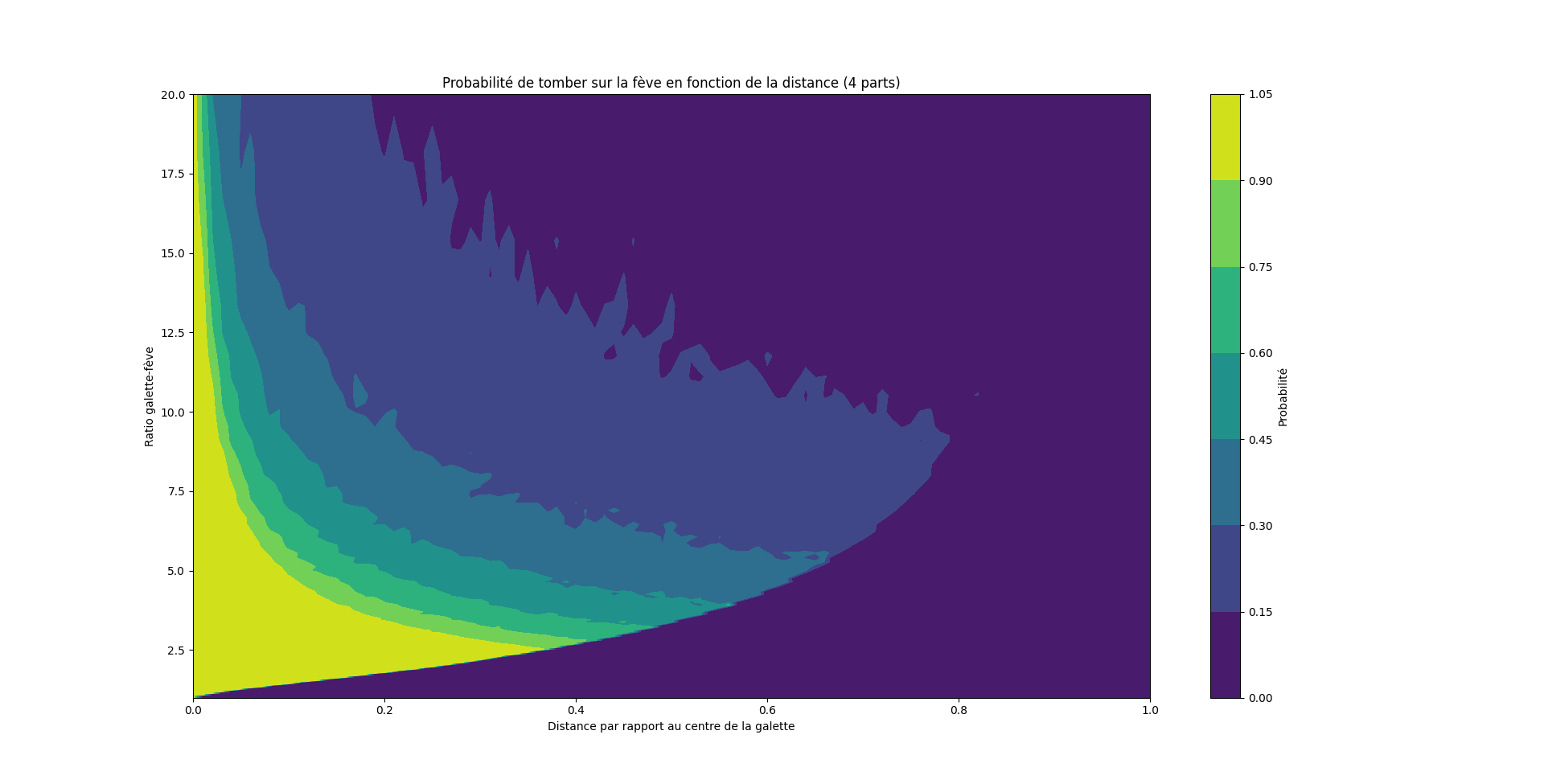
Étonnamment, placer la fève au-delà du milieu a un très fort impact sur la probabilité. Il vaut mieux la placer 20% plus loin que d'en avoir une 20% plus petite.