Les probabilités sont parfois déroutantes à cause de paradoxes que l'on rencontre. Bien entendu, tout paradoxe peut s'expliquer. Certains sont étonnants car ils choquent le "bon sens commun"; nous signalons le paradoxe des ascenseurs et celui bien plus étonnant des trois portes . Quand on aborde les situations où intervient une infinité de cas possibles les choses se corsent.

Nous décrirons le plus célèbre d'entre eux, le paradoxe de Bertrand .

Etant donné une corde tracée au hasard dans un cercle, quelle est la probabilité que sa longueur soit supérieure au côté du triangle équilatéral inscrit

• 1 ^ère solution: 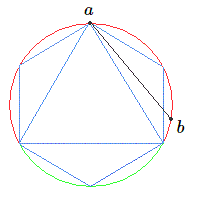On trace une corde à partir d'un point \(a\) choisi sur le cercle (on peut toujours par rotation amener une extrémité de la corde sur ce point). On sait que le côté de l'hexagone régulier inscrit vaut le rayon du cercle. Par conséquent pour tout choix de l'extrémité \(b\) de la corde compris dans la partie rouge du schéma, la corde sera plus petite que le côté du triangle équilatéral; pour \(b\) choisi dans la partie verte elle sera plus grande. Comme il est clair que l'arc vert mesure 120° et l'arc rouge 240°, la probabilité cherchée vaut \(1/3\).
• 2 ^e solution: 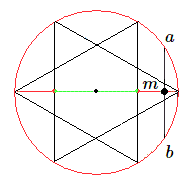On choisit un diamètre et par rotation on amène la corde dans la direction perpendiculaire à celui-ci. On construit alors la corde en partant d'un point m quelconque du diamètre. A partir de chaque extrémité du diamètre choisi, construisons le triangle équilatéral ayant un sommet en ce point. Les côtés perpendiculaires au diamètre le coupent au 1/4 et au 3/4 de sa longueur. Pour tout point m situé dans la région verte entre ces deux extrémités la corde sera supérieure au côté du triangle équilatéral; par contre dans la région rouge elle sera plus petite. Comme ces deux régions ont la même longueur, la probabilité vaut \(1/2\).
• 3 ^e solution: 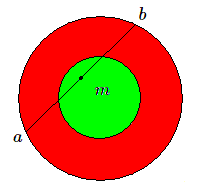On choisit un point \(m\) quelconque intérieur au cercle comme milieu de la corde à tracer. On sait que la distance du milieu du côté du triangle équilatéral au centre du cercle est égale à la moitié du rayon de celui-ci. Il en résulte que si le point \(m\) est dans la région verte intérieure au petit cercle, la corde sera plus grande que le côté du triangle équilatéral; par contre si le point \(m\) est à l'extérieur du petit cercle, dans la partie rouge, la corde sera plus petite. Comme le rayon du petit cercle vaut la moitié du rayon du grand cercle l'aire du petit cercle est le quart de l'aire du grand cercle; la probabilité vaut donc \(1/4\).

Ce paradoxe est devenu célèbre surtout par les valeurs simples obtenues \((1/2, 1/3, 1/4)\). Mais il existe bien d'autres paradoxes du même type où les "solutions" sont bien plus simples. Nous en donnons un exemple:

• Choisissons un réel compris entre 0 et 10. Quelle est la probabilité qu'il soit supérieur à 5 ? la réponse est "évidemment" 1/2.
• Choisissons un réel compris entre 0 et 100. Quelle est la probabilité que sa racine carrée soit supérieure à 5 ? Comme il doit être supérieur à 25, la probabilité vaut "évidemment" 3/4.

Et pourtant, si on réfléchit un instant, les deux questions posées sont les mêmes. En effet si un réel est compris entre 0 et 100, sa racine carrée positive est comprise entre 0 et 10, et réciproquement !

Le problème réside dans le fait que, lorsque des ensembles sont infinis il est difficile de les mesurer. On voit dans notre exemple que l'on peut affirmer qu'il y a autant de réels compris entre 0 et 10 que de réels entre 0 et 100. Pire ! Il y a autant de réels positifs que de réels compris entre 0 et 1; alors 1 = infini ? Un petit schéma le montre clairement.

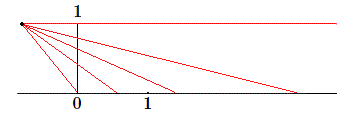
La réponse à de telles questions nécessite d'avoir au préalable défini la manière dont on allait mesurer les ensembles en question. C'est suite à l'embarras provoqué par de telles questions que Kolmogorov a été amené à donner une axiomatique pour le calcul des probabilités.