Un quart de la population a été vacciné contre une maladie contagieuse. Survient une épidémie. On constate que parmi les malades on trouve en moyenne un vacciné pour quatre non vaccinés, et parmi les vaccinés un malade sur douze.

On voit évidemment que le vaccin ne protège pas entièrement; c'est le cas pour la plupart des vaccins. Mais, quand même, il y a pas mal de malades parmi les vaccinés ! Alors la question se pose: "Le vaccin est-il efficace ?"

Pour qui connaît un peu de théorie, le problème n'est pas difficile. Il fait appel à la formule de Bayes, qui donne la probabilité d'un événement B sous condition qu'un événement A soit réalisé. Voyons comment s'introduit cette formule.

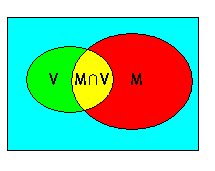Soient deux événements V et M que nous représenterons de la manière la plus générale. La probabilité de V est la mesure de l'ensemble V ; de même la probabilité de M est la mesure de l'ensemble M . Si on cherche la probabilité \(p\) ( M|V ) de M sachant que V est réalisé, on élimine les événements pour lesquels V n'est pas réalisé. La probabilité \(p\) ( M|V ) est le rapport entre la mesure de V \(\cap\) M et celle de V .

On obtient la célèbre formule de Bayes:

Compte tenu de la symétrie du premier membre \(p\) ( V \(\land M \))=\(p\) ( M \(\land\) V ) on a:

\(p\) ( M|V ).\(p\) ( V ) = \(p\) ( V|M ).\(p\) ( M )

Dans le problème posé, soit V l'événement "être vacciné" et M celui "être malade"; les événements contraires seront notés par \(\lnot \) V et \(\lnot \) M . On a vacciné un quart de la population, donc \(p\) ( V )\(=1/4\); donc \(p(\lnot \) V \()=3/4\). Utilisons à présent le fait que parmi les vaccinés, un sur douze avait contracté la maladie. Cela nous donne \(p\) ( M|V ) \(=1/12\). De plus, parmi les malades, on trouve en moyenne un vacciné pour quatre non vaccinés. Cela se traduit par : \(p\) (V|M) \(=1/5\); il en résulte que \(p(\lnot \) V|M \() =4/5\). Utilisons la relation \(p\) (V|M) .\(p\) (M) = \(p\) ( M|V ).\(p\) (V) qui donne après remplacement: \(1/5.p\) (M) \(=1/12.1/4\) c'est à dire \(p\) ( M ) \(=5/48\).

L'efficacité du vaccin revient à comparer: la probabilité \(p\) ( M|V ) d'être malade ayant été vacciné la probabilité \(p\) ( M |\(\lnot\) V ) d'être malade sans avoir été vacciné.

Il reste donc à, calculer \(p\) ( M |\(\lnot \) V ). On a \(p\) ( M |\(\lnot \) V ).\(p\) (\(\lnot \) V ) = \(p\) (\(\lnot\) V|M ).\(p\) ( M ) qui donne, après remplacement \(p\) ( M |\(\lnot \) V )\(.3/4=(4/5)(5/48)=1/12\), d'où \(p\) ( M \(\lnot \) V )\(=1/9\). On savait que \(p\) ( M|V )\(=1/12\) et on en conclut que le vaccin n'est pas très performant.

Mais il suffit parfois d'un petit schéma pour résoudre le problème plutôt que d'appliquer mécaniquement des formules (dont on ne se rappelle pas toujours avec précision).

Représentons l'ensemble de la population par un carré de côté \(1\) et séparons les vaccinés et les non-vaccinés de telle manière qu'il y ait (en surface) \(1/4\) de vaccinés pour \(3/4\) de non-vaccinés.

Dans chacun des deux groupes séparons les malades en respectant les données du problème (chez les vaccinés \(1\) malade sur \(12\) et \(1\) vacciné pour \(4\) non-vaccinés).

Qu'observons-nous ?

Les vaccinés sont représentés par un rectangle (vert) de \(1\) sur \(1/4\) et les non-vaccinés par un rectangle (bleu) de \(1\) sur \(3/4\). Parmi les vaccinés les malades sont représentés (en jaune) par un rectangle de \(1/12\) sur \(1/4\) (1 malade sur 12). L'aire vaut donc 1/48 (c'est la probabilité \(p\) ( V \(\cap\) M ) d'être malade bien que vacciné). Comme chez les malades il y a \(1\) vacciné pour \(4\) non-vaccinés, l'aire des malades non vaccinés vaudra \(4/48=1/12\); ils seront donc représentés par un rectangle (rouge) de hauteur \(3/4\) et la base vaudra donc \(1/9\).

La probabilité \(p\) ( M |\(\lnot \) V ) d'être malade, si on n'est pas vacciné, est donc de \(1/9\). La probabilité \(p\) ( M|V ) d'être malade, étant vacciné, est de \(1/12\). Le vaccin fait chuter la probabilité de \(1/9\) à \(1/12\), autrement dit il fait passer le nombre de malades de \(4\) à \(3\). Donc on peut dire que son efficacité est de \(25\)%, ce qui n'est pas fameux.

Encore plus simple !

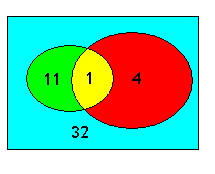
Reprenons le diagramme général en reportant deux sous-ensembles: les vaccinés et les malades. On nous dit que sur 12 vaccinés il y a 1 malade. Notons 1 dans l'ensemble V \(\cap \) M et le reste 11 dans l'ensemble V \(\cap\lnot \) M . Comme l'ensemble V mesure 12 et représente \(1/4\) de la population, le reste \(\lnot V\) mesurera 36. L'autre information dit que sur 5 malades il y a statistiquement 1 vacciné. L'ensemble M mesure \(5\) et nous pouvons porter \(4\) dans le sous-ensemble \(\lnot V\cap \) M . Il suffit de compléter le reste pour obtenir un total de \(48\).

Conclusion: chez les vaccinés \(1\) malade sur \(12\), chez les non-vaccinés \(4\) malades sur \(36\) (ou \(1\) malade sur \(9\)): le vaccin est assez peu efficace.

Et après ces calculs et ces dessins, n'êtes-vous pas plutôt convaincu de l'efficacité des schémas ?...