Une idée amusante pour fabriquer des bagues ou des colliers, consiste à utiliser des formes géométriques différentes: sphères, cylindres,...

On pourrait également essayer d'employer d'autres formes simples et en particulier, des polyèdres, notamment des tétraèdres. Mais comment les assembler ? Tout simplement par leurs arêtes autour desquelles ils pourront se mouvoir. Pourtant, certains problèmes vont rapidement se poser : il faut s'assurer que leur nombre soit suffisant pour éviter qu'ils ne coincent.

Si nous utilisons des tétraèdres réguliers, il en faudra assez bien : trois, quatre, cinq ne suffiront pas. Par contre, 6 tétraèdres permettent de refermer l'anneau mais malheureusement, cela coince ! A partir de 8 tétraèdres réguliers cela fonctionnera. Pourtant, avec 6 tétraèdres, nous n'étions pas loin de réussir. N'abandonnons pas si vite. Pour y remédier, conservons les arêtes "charnières" et étirons les arêtes "libres" de manière à augmenter le diamètre de l'anneau. Evidemment, les tétraèdres ne resteront plus réguliers, mais semi-réguliers en ce sens qu'ils auront deux arêtes opposées égales (les pivots) et les 4 autres arêtes égales également. Il est évident que si celles-ci sont suffisamment grandes, tout se passera bien.

Essayons de voir à partir de quel moment cet anneau, appelé kaléidocycle, pourra varier librement sans malencontreux coincement.

Voici la solution.

Mais... comment y sommes-nous arrivés ? Quelle longueur avons-nous choisie pour les arêtes libres ?

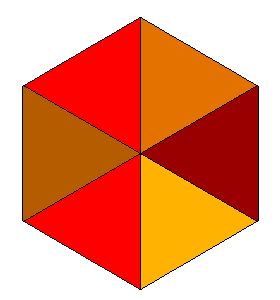
Pour cela, plaçons-nous dans la situation critique ; la voici en perspective :

Si nous regardons l'objet par le dessus, nous voyons un hexagone régulier: Dans cet hexagone, trois des arêtes passant par le centre - les "charnières" - sont vues en vraie grandeur car elles sont parallèles au plan horizontal. Soit \(L\) leur longueur. Les trois autres arêtes passant par le centre sont inclinées et donc raccourcies. Quant aux six arêtes formant le contour de l'hexagone, elles sont toutes vues en raccourci, mais elles sont bien intéressantes. Une arête représente un triangle, car cette face d'un tétraèdre est située, par raison de symétrie, dans un plan vertical. Sa longueur vue, \(L\), vaut exactement la hauteur relative de ce triangle par rapport au côté "charnière". Par conséquent, les faces sont toutes des triangles isocèles dont la base est égale à la hauteur correspondant à cette base.

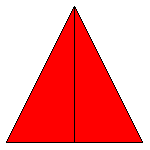
La base de ce triangle isocèle vaut \(L\) et, par le théorème de Pythagore, on voit que les côtés égaux ont une longueur égale à \(L\sqrt{5}/2 = 1.118...L\). Voila ainsi la plus petite possibilité afin que l'anneau puisse tourner librement sans coincer.

Nous vous conseillons toutefois de ne pas confondre "anneau" et "bague" ; vous risqueriez de vous coincer le doigt !