Rappelons brièvement la manière dont on calcule le PGCD de deux naturels à l'aide de l'algorithme d'Euclide.

Si \(a\) et \(b\) sont deux naturels avec \(a>b\), on divise \(a\) par \(b\). Si le quotient est exact, \(b\) est le PGCD; sinon on obtient un reste \(c

En analysant cet algorithme on se rend compte que le fait que \(a\) et \(b\) soient deux naturels n'est pas essentiel. En effet, effectuer un quotient revient à soustraire plusieurs fois et il n'y a pas de reste lorsque le quotient est un entier. L'algorithme peut donc s'appliquer à plusieurs grandeurs de même nature par exemple 2 segments, 2 réels,...

En fait, on recherche une unité de mesure telle que les mesures des 2 grandeurs s'expriment par des entiers; il serait peut-être plus indiqué de parler de PGCM (plus grande commune mesure)! C'est l'opération que l'on effectue lorsque l'on calcule la fréquence \(\omega\) de la somme de 2 phénomènes périodiques: on recherche le PGCD des fréquences de chaque composante; \(a~\mathbf{cos~}\omega_1 t+b~\mathbf{cos~}\omega_2 t\) est une fonction périodique de période \(2\pi/\omega\) où \(\omega\) est le PGCD de \(\omega_1\) et \(\omega_2\).

Vu sous cet angle la recherche du PGCD prend un nouvel intérêt; alors qu'il était évidemment toujours défini dans le cas de 2 naturels, il n'est pas clair qu'il le soit dans le cas de 2 grandeurs, en particulier de 2 segments. De ce fait s'il existe, en mesurant les 2 grandeurs à l'aide du PGCD on obtient 2 naturels et le rapport de deux grandeurs est rationnel; elles sont dites commensurables. Dans le cas contraire il n'existe pas de PGCD (ou pas de plus grande commune mesure); elles sont incommensurables, et le rapport des 2 grandeurs est irrationnel. C'est sous cette optique que sont apparus les premiers irrationnels.

Voyons tout d'abord une manière de géométriser les choses. Soit un rectangle de côtés \(a\) et \(b\) avec \(a>b\). On se demande s'il est possible de paver le rectangle à l'aide de carrés tous égaux.

S'il en est ainsi on peut retrancher des carrés de côté b jusqu'à obtenir un rectangle de grand côté b et de petit côté c égal à a moins le plus grand multiple entier possible de b. On répète l'opération. Si à un certain moment elle se termine, on a trouvé (à la dernière étape) un carré, le plus grand carré, qui pave le rectangle. Le côté de ce carré est le PGCD de \(a\) et \(b\).

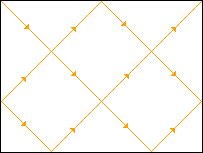
On peut visualiser les choses en imaginant un rectangle dont les côtés sont des miroirs; on introduit par un sommet un faisceau lumineux incliné à 45°; si par réflexions successives la lumière ressort par le sommet, alors le pavage par carrés est possible et les côtés a et b sont commensurables. Le nombre de réflexions sur chacune des paires de côtés parallèles du rectangle est égal au quotient de chacun des côtés par sa PGCM diminué d'une unité.