Le pied à coulisse est un instrument de mesure fort bien conçu. Il permet de mesurer la largeur extérieure ou intérieure d'un objet, en particulier les diamètres extérieur et intérieur d'un tuyau, la profondeur d'un objet, le tout grâce à une réalisation fort ingénieuse. Sur la gauche, on aperçoit au-dessus de la règle, deux pointes à bords extérieurs verticaux qui permettent de mesurer le diamètre intérieur d'un tuyau. En-dessous de la règle, deux bords extérieurs verticaux qu'on utilise pour mesurer le diamètre extérieur. Enfin, sur la droite de l'appareil, une tige qui permet de mesurer la profondeur.

Le résultat des mesures se lit sur la grande réglette horizontale qui est graduée en centimètres et divisée en millimètres ; il apparaît au-dessus du 0 de la petite échelle. Sur la figure, on peut lire la mesure obtenue : 3,5 cm ou 35 mm.

Ce n'est évidemment pas très précis. On voit qu'en réalité on dépasse un peu la graduation 35 mm. Dès lors, la question se pose : "Comment préciser ?" Et c'est là que réside le rôle de cette petite échelle située en-dessous de la règle dont nous n'avions pas encore parlé.

Prenons un cas concret. Supposons que nous obtenions, comme dans la figure ci-dessous, une mesure comprise entre 14 et 15 mm. Comment évaluer le nombre de dixièmes de millimètre ? Certainement plus que 1 mais bien moins que 9. Certes, il "suffirait" de subdiviser la graduation; malheureusement c'est impossible du fait de l'épaisseur des traits. Mais alors comment préciser ?

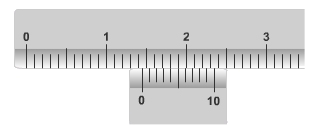
Supposons que ce soit 14,1 mm. Il suffira d'ajouter à la mesure 9/10 de mm pour arriver à une graduation exacte. Si c'était 14,2 mm, cela ne suffirait pas. Pour rattraper la différence, il faudrait ajouter deux graduations de 9/10 de mm. Et ainsi de suite.

Voila le rôle de cette petite échelle située en-dessous de la règle. Chacune de ses graduations vaut 0,9 mm; elle est donc constituée d'une division de 9 mm en 10 parties égales. Lorsqu'il y a coïncidence d'une de ses graduations avec une de celle de la règle, on obtient le nombre de dixièmes de mm à ajouter. Dans l'exemple ci-dessus, il semble que ce soit 4 et on obtient donc une mesure de 14,4 mm. Toutefois, on est également très proche de la 5e et on peut donc dire que la distance mesurée est comprise entre 14,4 et 14,5 mm. Ce dispositif permet d'avoir une mesure au dixième de millimètre près.

Plus généralement, on peut encore augmenter la précision comme cela se voit sur la première image du pied à coulisse. Sur cet instrument, la précision est poussée jusqu'au 1/40e mm. En effet, si, pour obtenir une précision au dixième de millimètre, il fallait subdiviser 9 mm en 10 parties, on peut obtenir une précision au 1/40 mm en subdivisant 39 mm en 40 comme sur la figure du pied à coulisse ci-dessus !

Une remarque : pour des raisons pratiques évidentes, la petite échelle reste toujours graduée en dixièmes de millimètre. Sur la figure, on voit que la graduation ne va pas de 1 à 40 mais est fixée de 1 à 10; la subdivision plus fine correspond à 1/40e de millimètre.

Cette merveille technologique date de plus de ... 500 ans ! Appelée en français vernier du nom de Pierre Vernier (1580-1637), mathématicien de la Franche-Comté (qui n'appartenait pas encore à la France !), elle est également connue sous le nom de nonius du nom de l'astronome portugais Pedro Nunes (1502-1578) qui en utilisait une version moins pratique. Bien entendu, les mesures métriques n'existaient pas encore (il a fallu attendre la Révolution et le système métrique) mais ces techniques étaient essentiellement utilisées en astronomie pour les mesures d'angle (système sexagésimal), un domaine où une très grande précision était indispensable. Les graduations étaient gravées sur des bords circulaires des instruments.