Les vacances approchent et avec elles les traditionnels "bouchons".

Voila une réalité tout à fait concrète qui se prête à mathématisation. Comme dans tout modèle, la réalité est tellement complexe qu'il faudra faire quelques hypothèses simplificatrices (dont certaines pourraient éventuellement être levées par après). Nous supposerons donc que toutes les voitures sont pareilles, roulent à vitesse constante et à distance constante. Schématiquement voici la situation:

Quels sont les problèmes ? Tout d'abord on veut avoir un débit maximum, c'est-à-dire que le plus grand nombre possible de voitures s'évacuent. Une manière de faire est de rouler très vite. Mais alors le risque de collision augmente. Il faut donc réserver une distance suffisante entre deux voitures consécutives. Si les voitures roulent très lentement, cette distance pourra être fort courte, mais comme la vitesse est faible peu de voitures s'écouleront. Donc il faut augmenter la vitesse des voitures, mais alors augmenter la distance entre elles. On voit qui si on augmente trop la vitesse, comme la distance de sécurité augmente encore plus, en fin de compte le débit se ralentira. Il s'agit de trouver la vitesse optimale. Mettons tout cela en forme.

Appelons \(v\) (en km/h) la vitesse des voitures, \(l\) (en m) la longueur d'une voiture et \(L\)(en m) la distance entre les arrières de deux voitures consécutives. A ces variables il faudra encore ajouter D, le débit, et \(t\), le temps de réflexe nécessaire pour freiner.

Qu'est-ce que le débit D ? C'est le nombre de voitures qui franchissent une ligne fixe dans un intervalle de temps \(T\) (généralement mesuré en heures). La première voiture roule à une vitesse \(v\) et parcourt donc pendant le temps \(T\) heures la distance de \(vT\) km; comme les voitures se suivent à une distance \(L\) (en m) et au bout de \(T\) heures il y aura \(vT\) km/\(L\) m = 1000\(vT/L\) voitures qui seront passées. Notons \(D\) le débit par heure; il est donc proportionnel à \(vL\); désignons par \(C\) ce rapport. On a donc \(D = Cv/L\). Nous ne pouvons évidemment pas jouer sur la longueur \(l\) des voitures, mais bien la distance \(L\) entre voitures. Toutefois cette distance ne peut être inférieure à la distance de sécurité nécessaire pour le freinage.

Un freinage efficace doit pouvoir immobiliser le véhicule, c'est-à-dire annuler son énergie cinétique. On sait que l'énergie cinétique vaut \(mv^2 /2\) et donc la distance de sécurité contiendra une partie proportionnelle au carré de la vitesse. Quelle sera cette distance de freinage ? A la partie proportionnelle au carré de la vitesse il faudra ajouter la distance parcourue suite au temps de réaction. Cette distance devra être inférieure à \(L -l\) afin de ne pas heurter, avec l'avant, l'arrière du véhicule précédent. Cette distance vaut \(Kv^2 + tv\) et doit être inférieure ou égale à \(L-l\). On a donc (au mieux !) \(Kv^2 + tv + l = L\). Mais on sait que le débit \(D\) vaut \(Cv/L\); il vient donc:

\[D = Cv/(Kv^2 + tv + l)\]

Voila la relation entre la vitesse \(v\) des véhicules et le débit horaire \(D\). Comment optimiser les choses ?

Pour qui connaît les dérivées les choses sont simples: on recherche le maximum de \(D\) fonction de \(v\). On trouvera ainsi la vitesse optimale \(v_{opt}\) et le débit maximum \(D_{max} \). Annulons la dérivée première et nous obtenons: \(v^2 = l/K\). Comme la vitesse est positive \(v_{opt}= \sqrt(l/K)\).

Si nous ne connaissons pas les dérivées, réfléchissons un instant. Comment varie la fonction \(D\) en fonction de la vitesse \(v\) ? Ou plus simplement comment varie 1/\(D\) ?

\[1/D = (Kv^2 + tv + l)/Cv)\]

ou en effectuant la division :

\[1/D = Kv/C + t/C + l/Cv\]

C'est donc la somme d'une fonction linéaire : \((Kv + t)/C\) et d'une fonction inverse \(l/Cv\).

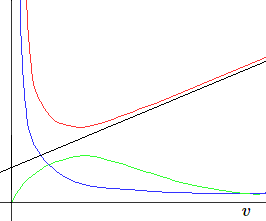
Représentons graphiquement en bleu une droite (de pente et d'ordonnée à l'origine positives) et une hyperbole. L'allure de la fonction \(1/D\) correspond donc schématiquement à la courbe tracée en rouge. Celle de \(D\) est représentée par celle dessinée en vert. Il y aura donc bien un débit maximum correspondant à une valeur optimale de la vitesse.

Au lieu de nous entêter à calculer la valeur du débit \(D\), nous pouvons plutôt nous intéresser à la vitesse \(v\). La relation entre \(v\) et \(D\) est:

\[KDv^2 + (Dt - C)v + Dl = 0\]

Nous en déduisons une équation du second degré qui nous permettra de calculer \(v\). À première vue, y aurait-il deux solutions pour la vitesse ?

Bien sur que non ; dans un problème réel, il faut tenir compte de la nature des grandeurs. La vitesse \(v\) doit être une grandeur positive ! Le produit des racines de l'équation du second degré donnée est positif, ce qui indique des solutions de même signe mais encore faut-il que la somme de ces solutions soit également positive. Cette somme vaut \(- (Dt - C)/KD\). La condition est donc \(Dt-C < 0\). À moins d'avoir de très mauvais réflexes, \(t\) est très petit et cette condition sera pratiquement toujours vérifiée.

Mais, au fait, est-on certain que l'équation possède des solutions ? Pour vérifier, calculons le discriminant qui doit être positif ou éventuellement nul:

\[(Dt - C)^2 - 4 K D^2 \ge 0\]    ou bien encore : \[(Dt - C)^2\ge 4 KD^2 l\]

et comme \(Dt - C\) doit être négatif :

\[Dt - C \le -2D \sqrt{Kl}\]

Ce résultat nous permet de calculer le débit \(D\):

\[D \le C/[t + 2\sqrt{Kl}]\]

et le débit sera maximum dans le cas de l'égalité.

\[D_{max} = C/[t + 2\sqrt{Kl}]\]

Mais dans ce cas, comme le discriminant est nul, l'équation possède deux solutions confondues. On obtient la vitesse optimale assurant le débit maximum:

\[v = -(Dt - C)/2KD    avec     D = D_{max} \]

d'où l'on déduit :

\[v_{opt} = \sqrt{l/K}\]

On connaît évidemment la longueur \(l\) des voitures, et la constante \(K\) peut être calculée en utilisant les données de la sécurité routière où l'on trouve les distances de freinage en fonction de la vitesse.

Lorsqu'on calcule le résultat numérique, on voit qu'il y a intérêt à suivre les conseils de "Bison futé", ou alors, à ne pas être pressé !