Si on parle beaucoup de l'équation du second degré on s'intéresse fort peu à l'ensemble des équations du second degré.

Une équation du second degré \( ax^2 + bx + c = 0\) est un triple de nombres \(a, b, c\) donnés à un facteur près (non nul évidemment). On reconnaît là des coordonnées homogènes dans le plan.

Si l'on préfère travailler avec des coordonnées cartésiennes, on peut remarquer que si l'on ne s'intéresse qu'aux "vraies" équations du 2e degré, le coefficient a n'est pas nul et l'équation peut s'écrire sous la forme \(x^2 + px + q = 0\). Une équation du deuxième degré proprement dite peut donc être représentée par un point de coordonnées \((p, q)\) dans le plan.

Il y a trois types d'équations du 2e degré suivant le signe du discriminant \(D = p^2 - 4q\). En particulier si \(p^2 = 4q\), les équations possèdent une racine double valant \(-p/2\). Elles sont représentées par les points d'une parabole.

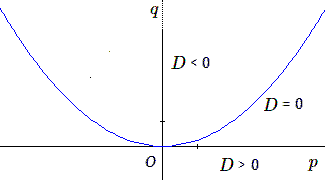
Les points intérieurs représentent les équations à \(D < 0\), c'est-à-dire les équations n'ayant pas de racine (réelle) ; les points extérieurs, celles à \(D > 0\), représentent les équations possédant 2 racines distinctes.

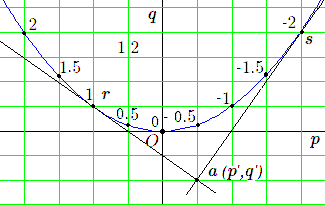
Soit \(a\) un tel point de coordonnées \((p', q')\) ; par \(a\) on peut mener 2 tangentes distinctes à la parabole \(p^2 - 4q = 0\). Ces tangentes ont deux points de contact \(r, s\) correspondant à deux équations du 2e degré ayant chacune une racine double (puisque \(p^2 - 4q = 0\)).

Il n'est dès lors guère difficile de vérifier que ces racines sont celles de l'équation du 2e degré considérée. On peut également le démontrer en remarquant que les deux points \(r, s\) de contact sont sur la polaire de \(a\) dont l'équation est \(pp' - 4(q + q')/2 = 0\). Il s'agit précisément de la condition de conjugaison des racines de deux équations du 2e degré ; les solutions (confondues) des équations correspondant aux points \(r\) et \(s\) sont donc les racines de l'équation correspondant au point \(a\), car deux points confondus sont conjugués par rapport à un couple de points distincts si et seulement s'ils sont confondus avec l'un d'eux.

On peut utiliser cette représentation pour construire un abaque permettant de résoudre graphiquement les équations du 2e degré.