Nous allons dans cette section traiter de manière très simplifiée un petit problème de génétique et tenter de donner une réponse à la question: Quelle est la probabilité que l'enfant de parents aux yeux bruns ait les yeux bleus ?

Tout d'abord un peu de biologie. Elle nous apprend que les caractères sont déterminés par des gènes portés par des chromosomes. Pour simplifier les choses, supposons qu'en ce qui concerne la couleur des yeux il n'existe que deux gènes (la réalité est bien plus complexe !): \(B\) (correspondant aux yeux bruns) et \(b\) (correspondant aux yeux bleus). Chez un individu les chromosomes se répartissent par paires dans le noyau. Si un des deux chromosomes porte un gène, son compagnon dans la paire porte un allèle du gène, c'est-à-dire un gène ayant la même fonction. Dans notre cas on pourra donc avoir 3 types d'individus: \((B,B)\), \((B,b)\) et \((b,b)\); on dit qu'on a 3 génotypes différents. Quand 2 gènes sont en présence le caractère apparent de l'individu dépend de ceux-ci; s'il est de génotype \((B,B)\) (resp.\((b,b)\)) il est clair que l'individu aura les yeux bruns (resp.bleus). Par contre s'il est de génotype \((B,b)\), alors l'un des gènes l'emporte sur l'autre, domine l'autre (qui est dit récessif); l'individu aura les yeux bruns.

En résumé, il y aura 2 phénotypes: yeux bruns et yeux bleus, correspondant aux génotypes \((B,B)\), \((B,b)\) d'une part et \((b,b)\) d'autre part.

Nous allons à présent voir comment se répartit la population fille d'une telle population; nous ferons l'hypothèse que le caractère considéré (couleur des yeux) est indépendant du sexe des individus.

Pour connaître le génotype des enfants d'un couple nous disposons de la loi de Mendel: un couple \((B,b), (B,b)\) aura 1/4 d'enfants \((B,B)\), 1/2 d'enfants \((B,b)\) et 1/4 d'enfants \((b,b)\). Schématiquement on a:

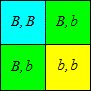
Les autres cas sont encore plus évidents. Nous pouvons représenter la situation sur un schéma et nous allons évaluer les proportions d'enfants de types différents en considérant les rapports des aires des rectangles.

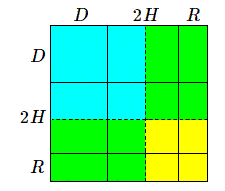
Si nous désignons par \(D\), \(2H\) et \(R\) (initiales de dominants, hybrides et récessifs) les proportions d'individus de type \((B,B)\), \((B,b)\) et \((b,b)\) on a évidemment: \(D + 2H + R = 1\). Pour les enfants :

$$ \begin{align} & \small D' = D^2 + 2.(1/2.D.2H) + 1/4(2H)^2 = (D + H)^2 \\ & \small H' = 2.(1/2.D.2H) + 2DR + 2(1/2.2H.R) + 1/2(2H)^2 = (D + H).(H + R) \\ & \small R' = 1/4(2H)^2 + 2.(1/2.R.2H) + R^2 = (H + R)^2 \end{align} $$

On voit que dans la population fille on a la relation \(D ': H' : R' = \alpha^2 : \alpha\beta : \beta^2\). On peut mieux comprendre la situation en disant que \(\alpha \) est la proportion de gènes \(B\) et \(\beta \) la proportion de gènes \(b\) dans la population mère.

À la génération suivante on aura:

$$ \begin{align} & \small D'' = (D' + H')^2 = (\alpha^2 + \alpha\beta)^2 = \alpha^2(\alpha + \beta)^2 = \alpha^2 \\ & \small R'' = (D' + R')^2 = (\alpha\beta + \beta^2)^2 = \beta^2(\alpha + \beta)^2 = \beta^2 \\ & \small H'' = \alpha.\beta \end{align} $$

La population s'est stabilisée; c'est la loi de Hardy-Weinberg. Remarquons que cette loi peut ne plus être valable dans d'autres conditions.

Revenons à présent à notre problème initial. L'hypothèse selon laquelle les parents ont tous deux les yeux bruns nous informe que leur génotype est soit \((B,B)\), soit \((B,b)\). Schématiquement on se trouve dans la région entourée en gras.

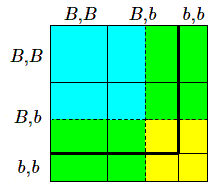
Nous pouvons aisément calculer dans la population fille, la proportion d'individus de type \((b,b)\); elle sera de:

\[ \frac{H^2}{(D+2H)^2}=\frac{\beta ^2}{(\alpha+2\beta)^2}=\frac{\beta ^2}{(1+\beta)^2} \]

Il nous suffit donc d'estimer \(\beta \). Pour cela nous savons que dans la population totale il y a un pourcentage de \(\beta^2\) personnes aux yeux bleus qui sont nécessairement de génotype \((b,b)\). On déduit ainsi la valeur de \(\beta \) et dès lors, on obtient la solution du problème posé.