Lorsque l'on veut avoir un renseignement géographique, on peut consulter un globe terrestre. Il s'agit là d'une excellente représentation de la réalité; toutefois elle est peu commode à utiliser. Il est préférable de consulter une carte que l'on dépose sur la table.

Malheureusement, cet avantage pratique est compensé par d'autres désavantages: la représentation est moins fidèle; certaines propriétés ont disparu. Mais, au fait, quelles sont les propriétés que l'on souhaiterait lors d'une représentation d'une sphère sur un plan?

Idéalement on souhaiterait que les aires, les plus courts chemins, les angles, les distances,... soient conservés. Malheureusement c'est impossible; une sphère a une aire finie, elle devrait donc être représentée sur un domaine fini du plan, mais alors qu'adviendrait-il du bord de ce domaine?

Si la représentation utilisée conserve les distances, elle conservera également les plus courts chemins; elle conservera aussi les angles (elle conserve les cercles et les distances); elle conservera aussi les aires (un petit "rectangle" deviendra un rectangle de même aire. En résumé une représentation idéale est une représentation qui conserve les distances, une isométrie.

Il n'existe malheureusement pas d'isométrie appliquant une sphère sur un plan. Par contre, il existe différentes représentations (projections) conservant soit les plus courts chemins, soit les angles, soit les aires. Nous allons les examiner successivement.

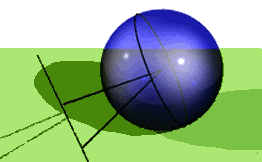Voici tout d'abord une représentation conservant les plus courts chemins. De telles représentations sont fort utiles pour la navigation aérienne. Sur une sphère, les plus courts chemins sont les grands cercles, en particulier les méridiens. Les plans de ces grands cercles ont pour intersection le centre de la sphère. Par conséquent si l'on projette la sphère sur un plan à partir de son centre, les grands cercles se projetteront selon des droites, plus courts chemins du plan. Malheureusement une telle projection appelée projection gnomonique, n'est pas une bijection; deux points antipodes ont la même projection. Il faut donc se borner à représenter une demi-sphère.

Venons-en à une projection conservant les aires (dite équivalente). Il en existe plusieurs qui ont toutes l'avantage de donner une idée plus précise des grandeurs des différents états. Nous décrirons la projection de Lambert.


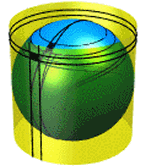
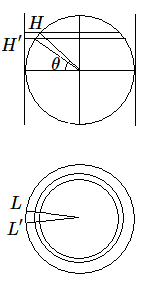
On projette la sphère sur un cylindre tangent à l'équateur, chaque point étant projeté à partir du point de l'axe Nord-Sud situé dans son parallèle. Cette projection conserve les aires. En effet, considérons sur la sphère un "petit" rectangle limité par deux méridiens et deux parallèles. Supposons-le situé à la latitude θ et de côtés L et H. Il se projette sur le cylindre selon un rectangle de côtés L' et H'. Les aires de ces deux rectangles valent donc L.H et L'.H'. Evaluons à présent L' et H' en fonction de L, H et de la latitude θ. On a respectivement: L' = L/cosθ et H' = H.cosθ. Il en résulte que les aires de ces deux rectangles sont égales, et par conséquent que la projection de Lambert est équivalente.

Passons enfin à une projection conservant les angles. Projetons une sphère (la terre) à partir d'un point (le pôle Nord, par exemple) sur un plan parallèle au plan tangent à la sphère au centre de projection (un plan parallèle au plan de l'équateur dans notre cas). Une projection de ce type est dénommée projection stéréographique.

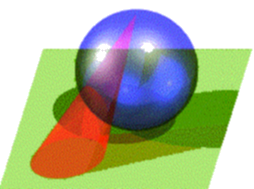
Remarquons qu'elle transforme un cercle en un cercle. En effet la projection du cercle se fait par l'intermédiaire d'un cône dont le sommet est au pôle Nord. Ce cône coupe la sphère en une courbe du quatrième degré; mais on en connaît déjà une partie, le cercle projeté; il reste donc une courbe du second degré, c'est-à-dire une conique (éventuellement dégénérée).
Dans quel plan est-elle située? Puisqu'il s'agit du pôle Nord (conique dégénérée en deux droites imaginaires conjuguées), il s'agit du plan tangent au pôle. Ce plan coupe donc le cône en un cercle de rayon nul et par conséquent tout plan parallèle, en particulier le plan de projection, coupera le cône projetant selon un cercle.

Il y a mieux!
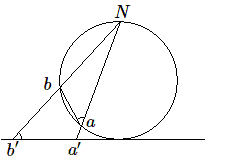Une simple considération des deux triangles Nab et Na'b' montre que les angles en a et en b' sont égaux.
Il en résulte que si l'on projette un angle (du plan tangent) sur le plan, les angles que font ces plans avec la génératrice du cône orthogonale à leur intersection seront égaux; dès lors par raison de symétrie les angles seront égaux.


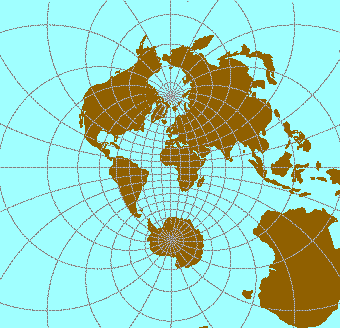Dans l'exemple ci-contre, la terre est projetée à partir d'un point de l'équateur situé aux antipodes de l'Afrique de l'Ouest. Les méridiens et les parallèles sont représentés par deux faisceaux de cercles ayant pour points limites les pôles Nord et Sud. Il s'agit d'une projection azimutale stéréographique équatoriale.

Une telle projection respecte les angles; elle était utilisée pour la navigation au compas.