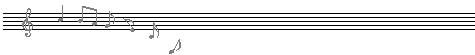Sur un instrument à cordes, lorsqu'une corde vibre successivement sur toute sa longueur, sur la moitié de la longueur, sur le tiers, le quart... de sa longueur, elle émet une suite de sons appelés harmoniques de la fondamentale (son produit lorsqu'elle vibre sur toute sa longueur).

Par exemple les harmoniques de la fondamentale Do sont successivement:

Do, Sol, Do, Mi, Sol, Sib, Do, Ré, Mi, ...

Ces harmoniques ont des fréquences qui sont des multiples entiers de la fréquence de la fondamentale. Ils s'harmonisent particulièrement bien avec celle-ci et forment la base du mode majeur , plus précisément Do majeur. En particulier, la deuxième harmonique est l'octave, la troisième est la quinte et la cinquième est la tierce majeure. On peut successivement entendre la fondamentale et ses \(n\) harmoniques jouées d'abord séparément et ensuite ensemble, le tout jusqu'à \(n=8\).

Si au contraire on se fixe un son initial (par exemple La) et que l'on cherche les sons ayant ce son comme harmonique on obtient successivement:

La, Ré, La, Fa, Ré, Si, La, Sol, Fa, ...

Cette fois-ci, ce sont les fréquences qui forment une suite harmonique et les sons obtenus forment la base du mode mineur , dans ce cas le La mineur. On peut successivement entendre la note de base (ce n'est pas la fondamentale, mais la dominante) et les n sons l'ayant pour harmonique d'ordre \(n\) joués d'abord séparément et ensuite simultanément, le tout jusqu'à \(n=8\).

C'est à partir des harmoniques, et plus précisément de la troisième harmonique (la quinte), que Pythagore a construit, par répétitions, une échelle de 12 sons: l'échelle des quintes:

Do, Sol, Ré, La, Mi,.......Sib, Fa, Do

Il faut toutefois remarquer que le "Do" obtenu après un cycle de \(12\) quintes a une fréquence \(3^12\) fois plus élevée que le Do initial, alors que les Do obtenus dans les octaves successives ont des fréquences qui sont multipliées par une puissance de \(2\). En fait le "Do" est approximativement celui obtenu au bout de \(19\) octaves; \(2^{19}\) vaut à peu près \(3^{12}\), le rapport des fréquences entre le "Do" et le Do vrai vaut \(0,9865...\) ce qui est appelé comma pythagoricien.

Par la suite, pour des raisons de meilleure consonance, on a tenté d'utiliser à la fois les quintes (la troisième harmonique) et les tierces majeures (la cinquième harmonique) ; cela a donné lieu à l'échelle de Zarlino. Si on choisit la fréquence de Do comme unité, tous les Do auront des fréquences égales à des puissances des \(2\); plus généralement si une note a une fréquence \(f\), tous les sons ne différant que par des octaves auront des fréquences égales à \(f.2^n\). Construisons les sons de la première octave, c'est-à-dire ceux ayant une fréquence comprise entre celle du Do (\(1\)) et du Do supérieur (\(2\)). Celle du Sol (le troisième harmonique) est \(3\) et le Sol de la première octave aura donc pour fréquence \(3/2\); celle de Mi (la cinquième harmonique) est \(5\), celle du Mi de la première octave sera donc \(5/4\); Fa est défini comme le son ayant Do comme troisième harmonique et sa fréquence est donc \(1/3\) (ou \(4/3\) pour le Fa de la première octave) et ainsi de suite...

Toutefois, aucune des solutions n'est rigoureusement satisfaisante lorsque l'on change de tonalité; on constate de faibles écarts de fréquence. Pour éviter cela, on a proposé, et on propose encore toujours, des solutions fantaisistes (nécessitant une division de la gamme en 53) distinguant une note dièsée de la suivante bémolisée, le demi-ton chromatique et le demi-ton diatonique, et bien d'autres! C'est pour mettre fin à cette impossibilité que Bach a proposé le tempérament égal, c'est-à-dire la division de l'octave en 12 sons tels que la fréquence d'un son soit celle du précédent multipliée par la racine douzième de 2. L'écart avec les harmoniques réelles est de toute manière extrêmement faible et reste en général en deçà du seuil de sensibilité de l'oreille humaine.

Ceux qui désirent plus de détails consulteront le document intitulé " Pourquoi n'ai-je jamais rien compris au solfège ", une rapide démystification de la théorie musicale.