Qu'est-ce qu'une valse ? Réponse : un air :

• à trois temps
• à mille temps
• de tous les temps

Cocher la bonne réponse.

Voilà un exemple de question à choix multiple. Ce type de questionnaire est souvent utilisé pour des raisons de commodité de correction et constitue un pis-aller lorsqu'on doit interroger un très grand nombre de personnes. Nous analyserons ici la structure mathématique associée à ces QCM.

Soit un questionnaire à choix multiple composé de \(N\) questions. Pour chacune des questions la personne testée a deux options: s'abstenir ou tenter d'y répondre; dans ce cas deux possibilités: se tromper ou répondre exactement. Désignons par \(V\) le nombre de questions correctement résolues, \(F\) le nombre de questions pour lesquelles la réponse est fausse et \(A\) le nombre d'abstentions. On a évidemment \(V+A+F=N\).

Des notes sont attribuées pour chaque question. Soit \(v\) le nombre de points pour une réponse exacte, \(f\) le nombre de points (éventuellement négatifs) pour une réponse fausse et \(a\) le nombre de points pour une abstention. Il est raisonnable de supposer que \(f\lt a\lt v\).

Les valeurs que l'on attribuera à ces trois grandeurs sont très subjectives; le démagogue donnera \(0\) pour une réponse fausse, ce qui lui permettra de donner une note positive à une feuille blanche! Il sera peut-être plus raisonnable de donner \(0\) pour une abstention (puisque la réponse est vide!). Quoi qu'il en soit, on peut toujours ajouter un même nombre aux notes \(f, a, v\) (faire une translation) de telle sorte que \(a=0\); cela ne modifiera pas le classement des individus testés. De plus on peut également choisir de prendre \(f=-1\) (effectuer une homothétie de centre 0). On peut en effet, sans affecter le classement, effectuer une transformation affine \(x\) vers \(\alpha x+\beta \) sur les notes en appliquant \(f\) sur \(-1\) et \(a\) sur 0. La valeur à attribuer à \(v\) est subjective et peut par exemple dépendre du nombre d'options proposées.

Comment représenter les différents questionnaires ?

Le problème dépend de deux paramètres (les trois nombres \(F, A, V\) sont liés par la relation \(V + A + F = N \)) et est donc représentable dans un plan. Mais quel plan? Le plan \((A, F)\), le plan \((V, F)\) ou le plan \((V, A)\) ? On hésite. Peut-être le plus réaliste est de ne pas tenir compte des abstentions (comme lors des élections) et de choisir \((V, F)\); bien que...

On peut raisonner autrement. On est en présence de trois variables \(F, A\) et \(V\), donc un questionnaire est représenté par un point de l'espace à 3 dimensions. Mais ces 3 nombres \(F, A, V\) sont liés par la relation \( V + A + F = N \).

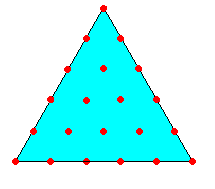Les points représentatifs sont donc situés dans un plan (le voilà le fameux plan !). De plus il existe des contraintes sur ces trois variables: \(V, F, A\) sont positifs. On se trouve donc à l'intérieur d'un triangle. En fait, on est ramené aux coordonnées trilinéaires de Möbius, conséquence du théorème de Viviani.

Voici, par exemple une représentation des réponses possibles dans le cas d'un QCM de 5 questions.

Revenons à notre problème. La note obtenue vaudra \(V.v+A.a+F.f\), c'est-à-dire une fonction linéaire des trois variables; on voit tout de suite que \(V.v+A.a+F.f=c\) est l'équation d'une droite. Il en résulte que si l'on fait varier \(c\) (la note), on obtient une famille de droites parallèles (s'il n'en était pas ainsi une même copie pourrait obtenir 2 notes différentes!!!).

Voici une représentation géométrique dans le cas où il y a 5 questions et où l'on attribue \(2\) points pour une réponse exacte, \(0\) pour une abstention et \(-1\) pour une erreur. 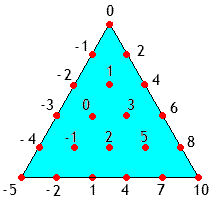Sur la figure on peut voir apparaître une série de paradoxes? Par exemple: il y a deux manières d'obtenir la note (peu brillante) de \(4/10\): ou bien on répond exactement à \(2\) questions et on fait l'impasse sur les \(3\) autres, ou alors on fait l'effort de répondre aux \(5\) questions mais malheureusement il n'y a que \(3\) réponses correctes. Il y a pire! Si l'on répond correctement à \(2\) questions et que l'on souhaite améliorer son score, une réponse fausse oblige à avoir une réponse correcte parmi les deux questions restantes.

Que faut-il faire pour réussir le test ? S'abstenir pour \(2\) questions et répondre correctement aux \(3\) autres, s'abstenir pour \(1\) question et faire au plus une erreur parmi les \(4\) autres, ou alors ne pas s'abstenir et faire au plus une erreur parmi les \(5\) questions. Que l'on réponde à \(4\) ou \(5\) questions, on voit que le "droit à l'erreur" n'est jamais que d'une seule erreur !

D'où proviennent ces paradoxes ? Tout simplement du fait que les variables \(F, A\) et \(V\) ne sont pas des réels mais bien des naturels. Les points représentatifs des divers questionnaires ne constituent pas tout l'intérieur du triangle, mais bien une famille de points (disposés agréablement aux sommets d'un pavage par triangles équilatéraux). Dès lors cette discrétisation est source de phénomènes curieux et parfois paradoxaux !