Quand nous lançons en l'air un objet il retombe (attention, pas toujours ! ... et si c'est un ballon gonflé à l'hélium ?)

Toutefois en conservant le même angle de tir, si nous le lançons avec plus de force, il ira plus loin . Faisons un petit schéma:

Mais ce dessin n'est pas très correct. En effet nous nous trouvons sur la terre, et celle-ci est sphérique. Un schéma plus correct serait celui-ci:

Ensuite, si nous regardons de plus loin, nous voyons qu'en déployant suffisamment d'énergie il pourra être possible d'envoyer l'objet avec une énergie telle qu'il retombe tellement loin, qu'en fait il ne revienne pas (immédiatement) sur la terre, mais qu'il continue à tourner et se soit satellisé !

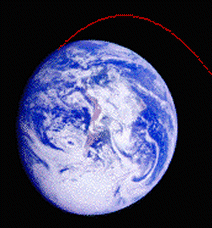
Le satellite est attiré par la terre selon la loi de Newton. La force d'attraction est proportionnelle à la masse m du satellite, à la masse M de la terre, inversément proportionnelle au carré de la distance des deux masses, le tout avec un facteur de proportionnalité (la constante de la gravitation).

Malheureusement nous ne connaissons pas immédiatement la masse de la terre et comment calculer cette fameuse constante ?

Heureusement nous pouvons nous en tirer autrement. A la surface de la terre cette force d'attraction est tout simplement le poids qui vaut mg et cette masse est attirée par la masse terrestre que l'on peut supposer concentrée au centre de celle-ci.

Energie potentielle = \(mgh\)

Pour contrebalancer l'énergie potentielle qui nous colle à la terre, il faut lancer la sonde avec une vitesse v suffisamment grande.

Si on souhaite faire échapper la sonde à l'attraction terrestre il faut que son énergie cinétique contrabalance son énergie potentielle.

Energie cinétique = \(mv^2/2\)

On doit donc choisir une vitesse telle que l'énergie cinétique soit supérieure ou égale à l'énergie potentielle; si on travaille à l'économie on prendra l'égalité.

On a donc l'équation:

\(mv^2/2 = mgh\)

d'où on tire:

A la surface de la terre \(g = 9,8 m/sec^2\) et \(h\) est le rayon terrestre c'est-à-dire \(6400 km\), donc \(6,4.10^6 m\). On peut calculer \(2gh = 2 x 9,8 m/sec^2 x 6,4.10^6 m = 125,44.10^6 m^2/sec^2\). La vitesse \(v\) nécessaire pour échapper à l'attraction terrestre est la racine carrée de \(125,44.10^6 m^2/sec^2\) et vaut \(11,2.10^3m/sec\) c'est-à-dire \(11,2 km/sec\).

Cette sonde spatiale nous enverra des informations, mais étant donné les distances, elles risquent d'être entâchées d'erreurs. Il faudra alors les décoder et les corriger.