Un célèbre jeu télévisé américain "Let's make a Deal" a suscité une énorme controverse, tant chez les téléspectateurs que dans le monde "scientifique".
Décrivons brièvement ce jeu très intellectuel:
Un candidat ayant brillament réussi une série d'épreuves "difficiles" gagne un prix; mais il peut le remettre en jeu pour tenter de gagner le super lot: une voiture. Il y a 3 portes (ou rideaux) et derrière l'un d'elles se trouve une voiture et derrière les deux autres une chèvre !?! (qu'on pourrait remplacer par un lot de consolation assez dérisoire). Le candidat choisit une porte. Pour augmenter le suspense le présentateur (qui sait où se trouve la voiture) ouvre une des deux autres portes et découvre une chèvre. Il demande alors au candidat s'il veut ou non modifier son choix.
Que doit faire le candidat?
La réponse est évidente; c'est du bon sens. Le candidat n'a obtenu aucune information, puisque parmi les deux portes restantes il y en a toujours une derrière laquelle se trouve une chèvre, qu'il maintienne son choix ou le modifie, dans tous les cas il a maintenant une chance sur deux de gagner la voiture.
Eh bien non ! Méfiez-vous du "bon sens" irréfléchi.
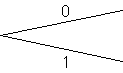
Supposons, sans nuire à la généralité que le candidat choisisse la porte A. Calculons la probabilité de trouver la voiture, après que le présentateur ait ouvert une des deux autres portes.
| la voiture est derrière | A | B | C | |
| le présentateur a ouvert B | 1/2 | 1/6 | 0 | 1/3 |
| le présentateur a ouvert C | 1/2 | 1/6 | 1/3 | 0 |
On voit donc que, quelle que soit la porte (B ou C) ouverte par le présentateur, le candidat a tout intérêt à modifier son choix: il double ses chances.
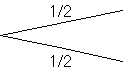
Un petit schéma rendra peut être les choses plus claires: Supposons, sans nuire à la généralité que la voiture est derrière la porte A.
| On ouvre: | prob. | ||||
|
B | 1/6 | |||
|
A | ||||
| C | 1/6 | ||||
|
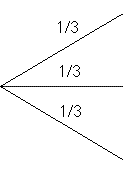
A | 0 | |||
| Choix du candidat | B | ||||
| C | 1/3 | ||||

|
A | 0 | |||
| C | |||||
| B | 1/3 |
Il est donc évident que le candidat, s'il modifie son choix, a maintenant 2/3 de gagner.
Pour ceux qui n'y croient toujours pas: de deux choses (non équiprobables) l'une:
- Le candidat a choisi la bonne porte (une chance sur trois). S'il modifie son choix il perd.
- Le candidat a choisi une mauvaise porte (deux chances sur trois). S'il modifie son choix il gagne.
Si vous n'êtes toujours pas convaincus, imaginez qu'il y a 100 portes, vous en choisissez une et le présentateur en ouvre 98 (derrière lesquelles il n'y a évidemment rien !)
Enfin pour les derniers sceptiques, remarquez que l'ouverture des portes n'apporte aucune information, puisque le présentateur sait où se trouve la voiture. Supposez donc que le présentateur n'ouvre aucune porte, mais vous propose :
- soit de conserver votre choix initial,
- soit de choisir l'ensemble de toutes les autres portes.
Il est vrai que la réponse au problème initial heurte le "bon sens", mais j'espère qu'à présent vous êtes convaincus. Sinon relisez les démonstrations un peu plus tard et consolez-vous en pensant qu'à l'heure actuelle il existe encore des mathématiciens qui n'ont pas compris !