Nous sommes sollicités de toutes parts pour tenter notre chance à des jeux de hasard plus attractifs les uns que les autres: loteries, casinos, salle de jeux etc. L'éventail de jeux proposés est très important et il importe de savoir à quoi on s'engage. Si les gains sont très clairement annoncés, rien n'est évidemment dit en ce qui concerne les risques de perte !

Supposons que l'état organise une tombola. Dix mille billets sont mis en vente au prix de 100 €. Les lots sont les suivants:

• les billets se terminant par un chiffre donné gagnent 200 €
• ceux se terminant par deux chiffres donnés gagnent 500 €
• ceux se terminant par deux autres chiffres donnés gagnent 500 €
• les billets se terminant par 3 chiffres donnés gagnent 1000 €
• et on tire encore 4 fois 3 chiffres donnant droit à 1000 €
• enfin le billet portant le numéro tiré au sort gagne 100000 €

Un milliardaire de passage se précipite et achète tous les billets. Il lui en coûte 10000 fois 100 € c'est-à-dire un million. Après le tirage il se présente pour retirer ses gains. Il a:

• 1000 billets qui gagnent 200 €
• 200 qui rapportent 500 €
• 50 qui gagnent 1000 €
• 1 billet qui gagne le super-gros lot de 100000 €

Il reçoit donc la somme de: 1000.200 € + 200.500 € + 50.1000 € + 100000 € soit 450000 € Tout déçu, il constate que chaque billet payé 100 € ne lui rapporte en moyenne que 45 € et que, tous comptes faits, si venant d'acheter les billets et sachant que l'espérance d'un billet est de 45 €, il aurait mieux valu trouver quelqu'un prêt à les lui racheter à 46 € pièce ! Il décide évidemment de ne plus jamais acheter un seul billet de tombola.

Prenons l'exemple du "bandit manchot", cette machine à sous munie d'un levier à actionner et qui laisse astucieusement l'autre main libre pour introduire les jetons dans la fente de la machine.

Le jeu est très simple: les trois roues, où figurent divers dessins, sont mises en mouvement sous l'action du levier. Après avoir tourné (pas trop longtemps pour que la machine soit rentable !) les roues s'arrêtent et trois dessins sont alignés.

Certaines combinaisons sont gagnantes; en particulier celles avec trois figures identiques. Toutefois pour ne pas décourager les "clients" on peut également gagner dans d'autres cas. Nous avons relevé les gains suivants :

• une cerise: la mise est rendue
• deux cerises gagnent 2 × la mise
• trois cerises rapportent 3 ×; la mise
• trois fruits gagnent 5 × la mise
• trois cloches rapportent 10 × la mise
• trois "sept" gagnent le gros lot: 50 × la mise

Quelles sont nos chances de gagner (ou plutôt de perdre) ? Statistiquement tous les arrangements de figures ont la même probabilité de sortir. Comme il y a 6 figures :

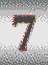
Sur chacune des trois roues il y a 6³=216 arrangements possibles.

Les arrangements qui ne comportent qu'une seule cerise sont au nombre de 75 (la cerise peut être à n'importe laquelle des trois positions et les deux autres figues peuvent être n'importe lesquelles des 5, d'où 3.5²=75). Par contre les arrangements comportant 2 cerises sont moins nombreux: la figure qui n'est pas une cerise peut être n'importe laquelle des 5 autres; de plus elle peut se situer à n'importe laquelle des 3 positions. Il y en a donc 15. Un seul de ces arrangements comporte 3 cerises, de même un seul 3 oranges, 3 prunes, 3 pastèques, 3 cloches et 3 "sept".

Notre milliardaire fait alors le raisonnement suivant: "Je vais jouer 216 fois, j'obtiendrai tous les arrangements possibles et je gagnerai donc : 75 fois un jeton + 15 fois 2 jetons + 1 fois 3 jetons + 3 fois 5 jetons + 1 fois 10 jetons + 1 fois 50 jetons, donc un total de 183 jetons.

Conclusion: Ce jeu est moins désavantageux que la loterie, mais pour 216 jetons mis en jeu je n'en récupère que 183. Je perds donc 33/216 ^e de ma mise." Ce raisonnement, bien qu'ayant une conclusion correcte est erroné. Il est clair qu'en jouant 216 fois on n'obtiendra pratiquement jamais tous des arrangements différents. (Au 216 ^e coup la machine se souviendrait-elle des 215 coups précédents ?

Pourtant, notre milliardaire est tout près de la vérité.

S'il joue \(n\) fois il aura \(n_1\) fois le gain \(g_1\), \(n_2\) fois le gain \(g_2\), ... et \(n_k\) fois le gain \(g_k\); toutes les autres fois il n'aura rien gagné. Il faut être bien conscient que son gain n'est autre que ce qu'il a reçu dont il faut déduire sa mise. Autrement dit, quand il perd le gain est négatif et vaut \(-m\). Au total il aura reçu \(\sum_{k=1}^n n_k.g_k\), et il aura dépensé \(nm\). En divisant par \(n\) on fait apparaître les fréquences \(n_k/n\) qui sont, à la limite, les probabilités \(p_k\) de l'événement \(k\) avec gain g_k; le gain moyen est donc la somme sur k gains g_k pondérés par leur probabilité soit donc :

\[ E =\sum_{k=1}^n p_kg_k \]

Il est évident que dans les jeux de hasard E est toujours négatif. Et paradoxalement \(E\) s'appelle l'"espérance" mathématique !

Si cette espérance est nulle, on dit alors que le jeu est équitable, honnête. Mais, pour autant n'y a-t-il aucun risque ?