Nous avons rencontré un joli polyèdre, le dodécaèdre qui doit sa renommée au nombre d'or qui lui est associé. Comment construire un tel polyèdre ? C'est particulièrement simple.

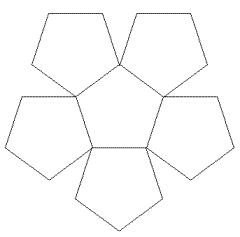
Partons d'une des faces, un pentagone. Sur chacun de ses côtés construisons un pentagone isométrique. Par pliage autour des côtés du pentagone initial, nous obtenons une petite coupelle: le fond est le pentagone initial et ses bords sont formés des pentagones isométriques précédemment construits. La réunion de deux coupelles donne naissance au dodécaèdre régulier.

Une manière assez spectaculaire de le réaliser consiste à partir du développement de deux coupelles.

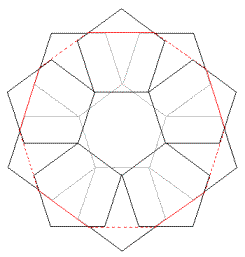
Il suffit de les superposer en les décalant d'un dixième de tour et d'utiliser un élastique (dessiné en rouge) qui passe au-dessus des faces de la partie supérieure et en-dessous de celles de la partie inférieure. De par son élasticité, lorsqu'on relâche le modèle, le dodécaèdre "jaillit" hors du plan de base; c'est déjà spectaculaire !

Cette manière de procéder est très classique, mais il est intéressant d'observer attentivement le résultat.

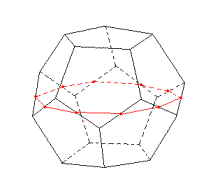
On obtient un dodécaèdre muni d'un lien élastique qui parcourt les 10 faces latérales et, par conséquent, évite 2 faces opposées : la base et la face supérieure. S'il n'y a pas de frottements et que l'on oublie l'épaisseur du lien, on obtient une courbe plane, un décagone qui passe par les milieux des 10 arêtes médianes.

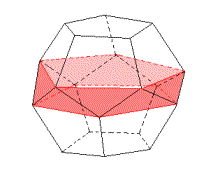
Une idée vient à l'esprit: augmenter la largeur de l'élastique utilisé jusqu'à ce qu'il passe par les 10 sommets de ces arrêtes. Qu'obtient-on alors ? Tout simplement un assemblage de 10 triangles isocèles dont les côtés égaux sont isométriques au côté du pentagone de départ et la base à une diagonale de ce pentagone; l'angle au sommet vaut 108° et les angles à la base 36°.

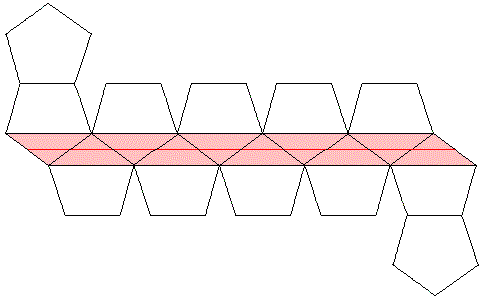
La situation peut être aisément visualisée à partir d'un des patrons du dodécaèdre. Dans celui où la face supérieure et la face inférieure ont été détachées, les 10 autres faces forment un assem-blage de 10 pentagones. Nous avons représenté en rouge vif le trajet de l'élastique et, en rouge pâle, les 10 triangles isocèles qui forment une bande à bords parallèles.

Mais en faisant cela, nous avons privilégié une paire de faces opposées du dodécaèdre initial ! Pas question de faire des jaloux.

Recommençons avec une autre paire de faces opposées, nous obtenons une nouvelle bandelette de papier (isométrique à la précédente). Faisons (voir la figure ci-dessus) de même avec toutes les paires de faces opposées. Comme le dodécaèdre possède, comme son nom l'indique, 12 faces, il y a donc 6 paires de faces opposées; par conséquent, nous obtiendrons 6 bandelettes de papier. Chacune recouvre partiellement chacun des 10 pentagones en un triangle, soit au total 60 triangles répartis équitablement sur les 12 faces, c'est-à-dire 5 par face.

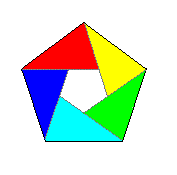
De là, l'idée de construire un dodécaèdre à partir de ces 6 bandelettes. Pour que le résultat soit joli, prenez soit un même papier (toutes les bandelettes sont identiques) ou alors 6 bandelettes de couleurs différentes. En plus, ajoutez-y une bonne dose de patience ! En fin de compte, le résultat en vaut la peine.

N'oubliez pas que les bandelettes se chevauchent et que, sur une même face, elles se recouvrent partiellement (voir la figure ci-dessus).

La construction ne nécessite donc ni colle, ni papier collant ! Remarquons également que cette figure est orientée. Selon le choix initial, vous obtiendrez l'une des deux figures finales images l'une de l'autre dans un miroir.

Bon travail et bon amusement.